Chuyên đề Giới hạn của dãy số 2023 hay, chọn lọc

Chuyên đề Giới hạn của dãy số

Phần 1: Giới hạn của dãy số và cách giải các dạng bài tập

1. Lý thuyết

a) Dãy số có giới hạn 0

Ta nói rằng dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số kể từ một số hạng nào đó trở đi, |u_n| nhỏ hơn số dương đó.

Kí hiệu:  hay lim u_n = 0 hay u_n → 0 khi n → +∞. 

b) Dãy số có giới hạn hữu hạn

Ta nói rằng dãy số (u_n) có giới hạn là số thực L nếu lim (u_n – L) = 0

Kí hiệu:  hay lim u_n = L hay u_n → L  khi n → +∞.

c) Dãy số có giới hạn vô cực

Dãy số (u_n) có giới hạn là +∞ khi n → +∞, nếu u_n có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Ký hiệu : lim u_n = +∞ hoặc u_n → +∞ khi n → +∞ 

Dãy số (u_n) có giới hạn là −∞ khi n → +∞ , nếu lim(−u_n) = +∞ 

Ký hiệu : lim u_n = −∞ hoặc u_n → −∞ khi n → +∞

d) Một vài giới hạn đặc biệt

 lim u_n = 0 ⇔ lim|u_n| = 0

; ,(k > 0, k ∈ ℕ^*); lim n^k = +∞,(k > 0, k ∈ ℕ^*)        

 

e) Định lý về giới hạn hữu hạn

* Nếu lim u_n = a và lim v_n = b và c là hằng số. Khi đó ta có :

lim(u_n + v_n) = a + b 

lim(u_n – v_n) = a – b 

lim(u_n v_n) = a.b 

 

lim(cu_n ) = c.a 

lim|u_n | = |a| 

 

Nếu u_n ≥ 0 với mọi n thì a ≥ 0 và  

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): 

Nếu  thì lim u_n = a.

Hệ quả: Cho hai dãy số (u_n) và (v_n): 

Nếu  thì lim u_n = 0.

f) Một vài quy tắc tìm giới hạn vô cực

* Quy tắc tìm giới hạn tích lim (u_nv_n)

Nếu lim u_n = L ≠ 0, lim v_n = +∞ (hay −∞). Khi đó: lim (u_nv_n)

lim un = L	lim vn	lim (unvn)
+	+∞	+∞
+	−∞	−∞
–	+∞	−∞
–	−∞	+∞

* Quy tắc tìm giới hạn thương    

lim un = L	lim vn	Dấu của vn
L	±∞	Tùy ý	0
L > 0	0	+	+∞
	0	–	−∞
L	0	+	−∞
	0	–	+∞

g) Tổng cấp số nhân lùi vô hạn

Xét cấp số nhân vô hạn u₁; u₁q; u₁q²; … u₁qⁿ; … có công bội |q|

Tổng của cấp số nhân lùi vô hạn là:   

2. Các dạng toán

Dạng 1. Tính giới hạn sử dụng một vài giới hạn đặc biệt

Phương pháp giải:

Sử dụng các giới hạn đặc biệt:

 lim u_n = 0 ⇔ lim|u_n| = 0

; ,(k > 0, k ∈ ℕ^*); lim n^k = +∞,(k > 0, k ∈ ℕ^*)        

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

Áp dụng công thức tính giới hạn đặc biệt, ta có:

 

Ví dụ 2: Tính các giới hạn sau:

 

c) lim (-0,999)ⁿ 

Lời giải

   

 

c) lim (-0,999)ⁿ = 0 vì |-0,999|

Dạng 2. Tính giới hạn hữu hạn của phân thức

Phương pháp giải: 

Trường hợp lũy thừa của n: Chia cả tử và và mẫu cho n^k (với n^k là lũy thừa với số mũ lớn nhất).

Trường hợp lũy thừa mũ n: Chia cả tử và mẫu cho lũy thừa có cơ số lớn nhất.

Sử dụng một vài giới hạn đặc biệt:

lim u_n = 0 ⇔ lim|u_n| = 0

; ,(k > 0, k ∈ ℕ^*); lim n^k = +∞,(k > 0, k ∈ ℕ^*)        

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau

 

Lời giải

 

 

     

 

Ví dụ 2: Tính các giới hạn sau:

 

 

Lời giải

   

Dạng 3: Tính giới hạn hữu hạn sử dụng phương pháp liên hợp

Phương pháp giải: Sử dụng các công thức liên hợp (thường sử dụng trong các bài toán chứa căn)

   

 

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

  

Ví dụ 2: Tính giới hạn sau:  

Lời giải

 

Dạng 4: Tính giới hạn ra vô cực dạng chứa đa thức hoặc căn thức

Phương pháp giải:

Rút bậc lớn nhất của đa thức làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu u_n = L ≠ 0, lim v_n = +∞ (hay −∞). Khi đó: lim (u_nv_n)

lim un = L	lim vn	lim (unvn)
+	+∞	+∞
+	−∞	−∞
–	+∞	−∞
–	−∞	+∞

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) lim (n⁴ − 2n² +3)

b) lim ( −2n³ + 3n − 1) 

c) lim (5ⁿ − 2ⁿ)  

Lời giải

a) lim (n⁴ − 2n² +3) =  

Vì lim n⁴ = +∞;   .

b) lim ( −2n³ + 3n − 1) =    

Vì lim n³ = +∞; 

c) lim (5ⁿ − 2ⁿ) =    

Vì lim 5ⁿ = +∞ và   .

Ví dụ 2: Tính các giới hạn sau

Lời giải

 

Vì    

   

Dạng 5: Tính giới hạn ra vô cực dạng phân thức

Phương pháp giải:

Rút bậc lớn nhất của tử và mẫu ra làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu lim u_n = L ≠ 0, lim v_n = +∞ (hay −∞). Khi đó: lim (u_nv_n)

lim un = L	lim vn	lim (unvn)
+	+∞	+∞
+	−∞	−∞
–	+∞	−∞
–	−∞	+∞

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

 

 

Ví dụ 2: Tính giới hạn sau  .

Lời giải

 

Dạng 6: Tính giới hạn sử dụng định lý kẹp

Phương pháp giải:

Sử dụng định lý kẹp và hệ quả của định lý kẹp

Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu  thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu  thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

   

 

Ví dụ 2: Tính các giới hạn sau :

 

Lời giải

Dạng 7: Giới hạn dãy số có công thức truy hồi

Phương pháp giải:

Cho dãy số (u_n) ở dạng công thức truy hồi, biết (u_n) có giới hạn hữu hạn

Giả sử lim u_n = a (a là số thực) thì lim u_n+1 = a.

Thay a vào công thức truy hồi. Giải phương trình tìm a. 

Ta được giới hạn của (u_n) là lim u_n = a.

Ví dụ minh họa:

Ví dụ 1: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và (u_n): .

Lời giải

Giả sử lim u_n = a, khi đó lim u_n+1 = a

Suy ra  ⇒ a² + 2a = 2a + 3 ⇔ a² = 3 ⇔     .

Do u₁ = 1 > 0, ∀n ∈ ℕ^* nên a > 0 ⇒   

Vậy  .

Ví dụ 2: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và (u_n):   .

Lời giải

Vì    

Giả sử lim u_n = a (a > 0), khi đó lim u_n+1 = a

Suy ra      

Vậy lim u_n = 2.

Dạng 8: Giới hạn của tổng vô hạn hoặc tích vô hạn

Phương pháp giải: 

* Rút gọn (u_n) (sử dụng tổng cấp số cộng, cấp số nhân hoặc phương pháp làm trội)

* Rồi tìm lim u_n theo định lí hoặc dùng nguyên lí định lí kẹp.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu  thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu  thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

   

 

Lời giải

 

   

Xét tử số: Ta thấy 1; 2; 3; 4; … ; n là một dãy số thuộc cấp số cộng có n số hạng với u₁ = 1 và d = 1. 

Tổng n số hạng của cấp số cộng:   

Xét mẫu số: Ta thấy 1; 3 ; 3² ; 3³ ; … ; 3ⁿ là một dãy số thuộc cấp số nhân có (n+1) số hạng với u₁ = 1 và q = 3.

Tổng (n + 1) số hạng của cấp số nhân:   

 

(Bằng quy nạp ta luôn có  n n ,∀n ∈ ℕ^* và 3ⁿ > 1, ∀n ∈ ℕ^* ⇒ 3ⁿ⁺¹ − 3ⁿ = 2.3ⁿ > 2 >1 ⇒ 3ⁿ⁺¹ − 1 > 3ⁿ).

Ví dụ 2: Tính giới hạn sau:    

Lời giải

Dạng 9: Tổng cấp số nhân lùi vô hạn

Phương pháp giải:

Tổng của cấp số nhân lùi vô hạn là:   

Ví dụ minh họa:

Ví dụ 1: Tính tổng

Lời giải

a)  là tổng cấp số nhân lùi vô hạn với u₁ = 1 và  

Nên  

b) S = 1 + 0,9 + (0,9)² + (0,9)³ +… là cấp số nhân lùi vô hạn với u₁ = 1 và q = 0,9.

Nên  

Ví dụ 2: Biểu diễn các số thập phân vô hạn tuần hoàn ra phân số:

a) a = 0,32111…  

b) b = 2,151515… 

Lời giải

a) Ta có a = 0,32111… =  

Vì  là tổng của cấp số nhân lùi vô hạn với    

Nên  

b) Ta có b = 2,151515… =    

Vì  là tổng của cấp số nhân lùi vô hạn với 

Nên  

3. Bài tập tự luyện

Câu 1. Trong các mệnh đề sau, mệnh đề nào là mệnh đề Sai?

 

Câu 2. Dãy số nào sau đây có giới hạn bằng 0?

 

Câu 3. Dãy số nào sau đây có giới hạn bằng 0?

Câu 4. Tính giới hạn   bằng

A. 0.                          B. 1.                          C. +∞ .                      D. 2.

Câu 5. Cho dãy số (u_n) với. Khi đó lim u_n bằng

       

Câu 6. Cho dãy số (u_n) với. Khi đó lim u_n bằng 

 

Câu 7. Tính   bằng:

A. +∞ .                      B. −∞ .                      C. -1.                         D. 0. 

Câu 8. Tính   bằng:

Câu 9. Tính   bằng:

 

Câu 10. Trong bốn giới hạn sau đây, giới hạn nào là 0 ?

 

Câu 11. Cho dãy số (u_n) được xác định bởi u₁ = 1,  với mọi n ≥ 1. Biết dãy số (u_n) có giới hạn hữu hạn, lim u_n bằng:

 

Câu 12. Giới hạn dãy số (u_n) với  là.

Câu 13. Chọn kết quả đúng của  

A. 5.                          B.   .                        C. −∞ .                      D. +∞ .

Câu 14. Tổng  bằng:

 

Câu 15. Biểu diễn số thập phân 1,24545454545… như một phân số:

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
C	D	D	A	A	B	B	C	D	D	B	A	D	B	B

Phần 2: Giới hạn của hàm số và cách giải các dạng bài tập

1. Lý thuyết

a) Giới hạn của hàm số tại một điểm:

* Giới hạn hữu hạn: Cho khoảng K chứa điểm x₀ . Ta nói rằng hàm số f(x) xác định trên K (có thể trừ điểm x₀) có giới hạn là L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K \ {x₀}  và x_n → x₀, ta có: f(x_n) → L. 

Kí hiệu:  hay f(x) → L khi x → x₀. 

Nhận xét: Nếu f(x) là hàm số sơ cấp xác định tại x₀ thì  

* Giới hạn ra vô cực: 

Hàm số y = f(x) có giới hạn dần tới dương vô cực khi x dần tới x₀ nếu với mọi dãy số (x_n): x_n → x₀ thì f(x_n) → +∞. 

Kí hiệu:  

Hàm số y = f(x)  có giới hạn dần tới âm vô cực khi x dần tới x₀ nếu với mọi dãy số (x_n): x_n → x₀ thì f(x_n) → −∞.

Kí hiệu: 

b) Giới hạn của hàm số tại vô cực

* Giới hạn ra hữu hạn:

– Ta nói hàm số y = f(x) xác định trên (a;+∞) có giới hạn là L khi x → +∞ nếu với mọi dãy số (x_n): x_n > a và x_n → +∞  thì f(x_n) → L. 

Kí hiệu:  .

– Ta nói hàm số y = f(x) xác định trên (−∞;b) có giới hạn là L khi x → −∞ nếu với mọi dãy số (x_n): x_n n → −∞ thì f(x_n) → L. 

Kí hiệu:  

* Giới hạn ra vô cực:

– Ta nói hàm số y = f(x)  xác định trên (a;+∞) có giới hạn dần tới dương vô cùng (hoặc âm vô cùng) khi x → +∞ nếu với mọi dãy số (x_n): x_n > a và x_n → +∞ thì f(x_n) → +∞ (hoặc f(x_n) → −∞). 

Kí hiệu:  

– Ta nói hàm số y = f(x)  xác định trên (−∞; b)  có giới hạn là dần tới dương vô cùng (hoặc âm vô cùng) khi x → −∞ nếu với mọi dãy số (x_n): x_n n → −∞ thì f(x_n) → +∞ (hoặc f(x_n) → −∞). 

Kí hiệu:  

c) Các giới hạn đặc biệt:

 

 với c là hằng số

 với k nguyên dương;

 với k lẻ, với k chẵn

 

d) Một vài định lý về giới hạn hữu hạn

* Nếu thì:

; nếu c là một hằng số thì    

 

* Nếu f(x) ≥ 0, thì  

Chú ý: 

– Các định lý về giới hạn hữu hạn của hàm số vẫn đúng khi thay x → x₀ bởi x → +∞ hoặc x → −∞. 

– Định lí trên ta chỉ áp dụng cho những hàm số có giới hạn là hữu hạn. Ta không áp dụng cho các giới hạn dần về vô cực.

* Nguyên lí kẹp

Cho ba hàm số f(x), g(x), h(x) xác định trên K chứa điểm x₀ (có thể các hàm đó không xác định tại x₀). Nếu  thì  

e) Quy tắc về giới hạn vô cực

Quy tắc tìm giới hạn của tích f(x)g(x)

L > 0	+∞	+∞
	−∞	−∞
L	+∞	−∞
	−∞	+∞

Quy tắc tìm giới hạn của thương    

		Dấu của g(x)
L	±∞	Tùy ý	0
L > 0	0	+	+∞
	0	–	−∞
L	0	+	−∞
	0	–	+∞

f) Giới hạn một bên

* Giới hạn hữu hạn

– Định nghĩa 1: Giả sử hàm số f xác định trên khoảng (x₀;b),(x₀ ∈ ). Ta nói rằng hàm số f có giới hạn bên phải là số thực L khi dần đến x₀ (hoặc tại điểm x₀) nếu với mọi dãy số bất kì (x_n) những số thuộc khoảng (x₀; b) mà lim x_n = x₀ ta đều có lim f(x_n) = L.

Khi đó ta viết:  hoặc f(x) → L khi x → x₀⁺.

– Định nghĩa 2: Giả sử hàm số f xác định trên khoảng (a;x₀), (x₀ ∈ ). Ta nói rằng hàm số có giới hạn bên trái là số thực L khi x dần đến x₀ (hoặc tại điểm x₀) nếu với mọi dãy bất kì (x_n) những số thuộc khoảng (a; x₀) mà lim x_n = x₀ ta đều có lim f(x_n) = L.

Khi đó ta viết:  hoặc f(x) → L khi x → x₀⁻.

– Nhận xét:

 

Các định lí về giới hạn của hàm số vẫn đúng khi thay x → x₀ bởi x → x₀⁻ hoặc x → x₀⁺.

* Giới hạn vô cực

– Các định nghĩa , ,và được phát biểu tương tự như định nghĩa 1 và định nghĩa 2.

– Nhận xét: Các định lí về giới hạn của hàm số vẫn đúng nếu thay L bởi +∞ hoặc −∞ 

2. Các dạng bài tập

Dạng 1: Giới hạn tại một điểm

Phương pháp giải:

– Nếu f(x) là hàm số sơ cấp xác định tại x₀ thì    

– Áp dụng quy tắc về giới hạn tới vô cực:

		Dấu của g(x)
L	±∞	Tùy ý	0
L > 0	0	+	+∞
	0	–	−∞
L	0	+	−∞
	0	–	+∞

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

 

Ví dụ 2: Tính các giới hạn sau:

 

Lời giải

a) Vì  nên  

Dạng 2: Giới hạn tại vô cực 

Phương pháp giải:

– Rút lũy thừa có số mũ lớn nhất

– Áp dụng quy tắc giới hạn tới vô cực

L > 0	+∞	+∞
	−∞	−∞
L	+∞	−∞
	−∞	+∞

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

   

Lời giải

 

 

Ví dụ 2: Tính các giới hạn sau:

Lời giải

a)  

Vì 

b)    

Vì  

Dạng 3: Sử dụng nguyên lý kẹp

Nguyên lí kẹp

Cho ba hàm số f(x), g(x), h(x) xác định trên K chứa điểm x₀ (có thể các hàm đó không xác định tại x₀). Nếu  thì  

Phương pháp giải:

Xét tính bị chặn của hàm số f(x) bởi hai hàm số g(x) và h(x) sao cho    

Chú ý tính bị chặn của hàm số lượng giác:

−1 ≤ sin x ≤ 1

−1 ≤ cos x ≤ 1

Ví dụ minh họa:

Ví dụ 1: Tính giới hạn của hàm số:

 

Lời giải

a) Ta có:    

Mà    

b) Ta có: 

Mà    

Ví dụ 2: Tính giới hạn của hàm số:  

Lời giải

 

 Ta có:    

Mà  

Dạng 4: Giới hạn dạng vô định  

Nhận biết dạng vô định  : Tính  trong đó f(x₀) = g(x₀) = 0. 

Phương pháp giải:

Để khử dạng vô định này ta phân tích f(x) và g(x) sao cho xuất hiện nhân tử chung là (x – x₀)

Định lí: Nếu đa thức f(x) có nghiệm x = x₀ thì ta có: f(x) = (x – x₀)f₁(x). 

* Nếu f(x) và g(x) là các đa thức thì ta phân tích f(x) = (x – x₀)f₁(x) và g(x) = (x – x₀)g₁(x). 

Khi đó , nếu giới hạn này có dạng  thì ta tiếp tục quá trình như trên.

Chú ý: Nếu tam thức bậc hai ax² + bx + c có hai nghiệm x₁ ; x₂ thì ta luôn có sự phân tích: ax² + bx + c = a(x – x₁) (x – x₂)

* Nếu f(x) và g(x) là các hàm chứa căn thức thì ta nhân lượng liên hợp để chuyển về các đa thức, rồi phân tích các đa thức như trên. 

Các lượng liên hợp:

 

* Nếu f(x) và g(x) là các hàm chứa căn thức không đồng bậc ta sử dụng phương pháp tách, chẳng hạn:

Nếu  thì ta phân tích:  

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

 

Ví dụ 2: Tính các giới hạn sau:

 

 

Lời giải

   

 

 

Dạng 5: Giới hạn dạng vô định  

Nhận biết dạng vô định    

 

Phương pháp giải:

– Chia tử và mẫu cho xⁿ với n là số mũ cao nhất của biến ở mẫu (Hoặc phân tích thành tích chứa nhân tử xⁿ rồi giản ước).

– Nếu u(x) hoặc v(x) có chứa biến x trong dấu căn thì đưa x^k ra ngoài dấu căn (Với k là mũ cao nhất của biến x trong dấu căn), sau đó chia tử và mẫu cho lũy thừa cao nhất của x.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

Lời giải

a)      

b)    

 

 

Ví dụ 2: Tính các giới hạn sau:

 

Lời giải

   

 

 

Dạng 6: Giới hạn dạng vô định ∞ − ∞ và 0.∞ 

Phương pháp giải:

– Nếu biểu thức chứa biến số dưới dấu căn thì nhân và chia với biểu thức liên hợp

– Nếu biểu thức chứa nhiều phân thức thì quy đồng mẫu và đưa về cùng một biểu thức

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

   

Lời giải

a) 

 

Ví dụ 2: Tính các giới hạn sau:

   

Lời giải

   

Dạng 7: Tính giới hạn một bên

Phương pháp giải:

Sử dụng quy tắc tính giới hạn tới vô cực

		Dấu của g(x)
L	±∞	Tùy ý	0
L > 0	0	+	+∞
	0	–	−∞
L	0	+	−∞
	0	–	+∞

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

 

Lời giải

 

Ví dụ 2: Cho hàm số  . Tính:

Lời giải

a)    

b)    

Dạng 8: Tìm tham số m để hàm số có giới hạn tại 1 điểm cho trước

Phương pháp giải:

Sử dụng nhận xét:    

– Tính giới hạn      

– Để hàm số có giới hạn tại x = x₀ cho trước thì . Tìm m.

Khi đó với m vừa tìm được, hàm số có giới hạn tại x = x₀ cho trước và giới hạn đó bằng L = 

Ví dụ minh họa:

Ví dụ 1: Cho hàm số . Với giá trị nào của a thì hàm số đã cho có giới hạn tại điểm x = 2?

Lời giải

Ta có  

Để hàm số có giới hạn tại x = 2 thì  ⇒ a = 1.

Vậy a = 1. 

Ví dụ 2: Tìm các giá trị thực của tham số m để hàm số để tồn tại  

Lời giải

Ta có  

Để hàm số có giới hạn tại x = 1 thì  ⇒ m − 3 = −2 ⇔ m = 1.

Vậy m = 1. 

3. Bài tập tự luyện

Câu 1. Tính   bằng:

A. -1                          B. −∞                       C. +∞                        D. -3       

Câu 2. Tính  bằng:

A. -2                          B.                         C.                        D. 2

Câu 3. Tính  bằng:

A. 3                           B. 1                           C. 4                           D. 2

Câu 4. Tính  bằng:

 

Câu 5. Tính  bằng:

 

Câu 6. Tính  bằng:

A. 4                           B. 3                           C. 0                           D. 1 

Câu 7. Tính  bằng

A. -2                          B. 1                           C. 2                           D. -1

Câu 8. Tính  bằng

A. −∞                        B. +∞                         C. 0                           D. 4

Câu 9. Tính  là:

A. 0                           B. +∞                        C. -2                          D. −∞

Câu 10. Tính    

A. -2                          B. −∞                        C. 0                           D. +∞ 

Câu 11. Cho . Giá trị của a là:

A. 6                           B. 10                         C. -10                        D. -6

Câu 12. Kết quả đúng của  bằng:

 

Câu 13. Trong các mệnh đề sau, mệnh đề nào đúng?

 

Câu 14. Cho . Tính .

A. 0                           B. 4                           C. +∞                         D. Không tồn tại

Câu 15. Tìm các giá trị thực của tham số m để hàm số  có giới hạn tại x = 0.

A. m = – 1                 B. m = 2                    C. m = -2                  D. m = 1

 

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
C	A	A	B	A	C	A	C	B	A	C	C	B	A	D

Phần 3: Hàm số liên tục và cách giải các dạng bài tập

1. Lý thuyết

a) Hàm số liên tục tại một điểm

Cho hàm số y = f(x) xác định trên K và x₀ ∈ K. 

 – Hàm số y = f(x) liên tục tại x₀ khi và chỉ khi  

 – Hàm số y = f(x) không liên tục tại x₀ ta nói hàm số gián đoạn tại x₀.

b) Hàm số liên tục trên một khoảng

 – Hàm số y = f(x) liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm x₀ của khoảng đó.

 – Hàm số y = f(x) liên tục trên [a; b] nếu nó liên tục trên (a; b) và ,    

c) Các định lý cơ bản

Định lý 1: 

 – Hàm số đa thức liên tục trên toàn bộ tập .

 – Các hàm số đa thức, phân thức hữu tỉ, lượng giác liên tục trên từng khoảng xác định của chúng.

Định lý 2: Cho các hàm số y = f(x) và y = g(x) liên tục tại x₀. Khi đó:

 – Các hàm số: y = f(x) + g(x); y = f(x) – g(x); y = f(x).g(x) liên tục tại x₀.

 – Hàm số  liên tục tại x₀ nếu g( x₀ ) ≠ 0.

Định lý 3: Cho hàm số y = f(x) liên tục trên [a; b] và f(a).f(b)

2. Các dạng toán

Dạng 1: Xét tính liên tục của hàm số tại một điểm

Loại 1: Xét tính liên tục của hàm số  tại x = x₀.

Phương pháp giải:

Bước 1: Tính f(x₀) = f₂(x₀). 

Bước 2: Tính 

Bước 3: Nếu f₂(x₀) = L thì hàm số f(x) liên tục tại x_0.

 Nếu f₂(x₀) ≠ L thì hàm số f(x) không liên tục tại x_0.

(Đối với bài toán tìm tham số m để hàm số liên tục tại x₀, ta thay bước 3 thành: Giải phương trình L = f₂(x₀), tìm m)

Ví dụ minh họa:

Ví dụ 1: Xét tính liên tục của hàm số sau tại điểm x = – 1.

 

Lời giải

Hàm đã cho xác định trên  .

Ta có: f(-1) = 3

 

Ta thấy    

Vậy hàm số liên tục tại x = – 1.

Ví dụ 2: Cho hàm số: . Tìm m để hàm số liên tục tại x = 1.

Lời giải

Hàm đã cho xác định trên [0;+∞) .

Ta có

f(1) = m².

 

Để hàm số liên tục tại x = 1 thì  

Vậy  

Loại 2: Xét tính liên tục của hàm số  tại x = x₀.

Phương pháp giải:

Bước 1: 

Tính f(x₀) = f₂(x₀).

Tính giới hạn trái:    

Tính giới hạn phải:    

Bước 2: 

Nếu L = L₁ thì hàm số liên tục bên trái tại x₀. 

Nếu L = L₂ thì hàm số liên tục bên phải tại x₀.

Nếu L = L₁ = L₂ thì hàm số liên tục tại x₀.

(Nếu cả 3 trường hợp trên không xảy ra thì hàm số không liên tục tại x₀)

    * Đối với bài toán tìm m để hàm số liên tục tại x₀ ta giải phương trình: L = L₁ = L₂. Tìm m.

Ví dụ minh họa:

Ví dụ 1: Cho hàm số  

Xét tính liên tục của hàm số tại x = -1.

Lời giải

Ta có: 

f(- 1) = = 2. (-1) + 3 = 1

 

Ta thấy  

Vậy hàm số gián đoạn tại x = – 1.

Ví dụ 2: Cho hàm số:  Tìm m để hàm số liên tục tại x = 1

Lời giải

Ta có:  

Khi đó:  

Hay:  (vì x² – 3x + 2 = (x – 2)(x – 1))

Ta có: f(1) = m

 

 Để hàm số liên tục tại x = 1 thì    

Khi đó: 1 = m = – 1 (vô lý)

Vậy không tồn tại m để hàm số liên tục tại x = 1.

Dạng 2: Xét tính liên tục của hàm số trên một khoảng

Phương pháp giải:

Bước 1: Xét tính liên tục của hàm số trên các khoảng đơn

Bước 2: Xét tính liên tục của hàm số tại các điểm giao

Bước 3: Kết luận.

Ví dụ minh họa:

Ví dụ 1: Cho hàm số  Xét sự liên tục của hàm số.

Lời giải

Hàm số xác định và liên tục trên (−∞;1) và (1;+∞).

Xét tính liên tục tại x = 1

f(1) = 2.1 = 2.

 

Ta thấy  nên hàm số liên tục tại x = 1.

Vậy hàm số liên tục trên  .

Ví dụ 2: Cho hàm số  Tìm m để hàm số liên tục trên [0;+∞).

Lời giải

Với x ∈ (0;9):  xác định và liên tục trên (0;9). 

Với x ∈ (9;+∞):  xác định và liên tục trên (9;+∞). 

Với x = 9, ta có   

 và   

Ta thấy  nên hàm số liên tục tại x = 9.

Với x = 0 ta có f(0) = m.

 

Để hàm số liên tục trên [0;+∞) thì hàm số phải liên tục tại x = 0

 

Vậy  thì hàm số liên tục trên [0;+∞) .

Dạng 3: Chứng minh phương trình có nghiệm

Phương pháp giải:

Sử dụng định lý: Cho hàm số y = f(x) liên tục trên [a; b] và f(a).f(b)

Chú ý: Đa thức bậc n có tối đa n nghiệm trên  .

* Chứng minh phương trình f(x) = 0 có ít nhất một nghiệm.

 – Tìm hai số a và b sao cho hàm số f(x) liên tục trên đoạn [a; b] và f(a).f(b)

 – Phương trình f(x) = 0 có ít nhất một nghiệm x₀ ∈ (a;b) 

* Chứng minh phương trình f(x) = 0 có ít nhất k nghiệm

 – Tìm k cặp số a_i; b_i sao cho các khoảng (a_i; b_i) rời nhau và f(a_i).f(b_i)

 – Phương trình f(x) = 0 có ít nhất một nghiệm  x_i ∈ ( a_i;b_i ).

Khi đó f(x) = 0 có ít nhất k nghiệm.

Ví dụ minh họa:

Ví dụ 1: Phương trình:  có bao nhiêu nghiệm thuộc khoảng (-1; 3). 

b) Phương trình  có bao nhiêu nghiệm.

Lời giải

a) Xét hàm số  liên tục trên [- 1; 3].

Ta có:  

Ta thấy:

f(- 1).f(0)

f(0).f(½) , phương trình có ít nhất 1 nghiệm thuộc (0;½) 

f(½).f(1) , phương trình có ít nhất 1 nghiệm thuộc (½;1) 

f(1).f(3)

Do đó phương trình có ít nhất 4 ngiệm thuộc khoảng (-1; 3). 

Mặt khác phương trình bậc 4 có tối đa bốn nghiệm.

Vậy phương trình có đúng 4 nghiệm thuộc khoảng (-1; 3).

b) Đặt . Khi đó phương trình đã cho có dạng 2t³ – 6t + 1 = 0 

Xét hàm f(t) = 2t³ – 6t + 1 liên tục trên .

Ta có f(- 2) = – 3, f(0) = 1, f(1) = – 3, f(2) = 5.

Ta thấy:

f(- 2).f(0) = – 3  0, phương trình có một nghiệm t₁ ∈ (−2;0). Khi đó x₁ = 1 − t₁³,x₁ ∈ (1;9).  

f(0).f(1) = – 3  0, phương trình có một nghiệm t₂ ∈ (0;1). Khi đó x₂ = 1 − t₂³,x₂ ∈ (0;1). 

f(1).f(2) = – 15  0, phương trình có một nghiệm t₃ ∈ (1;2). Khi đó x₃ = 1 − t₃³,x₃ ∈ (-7;0).

Do đó phương trình 2t³ – 6t + 1 = 0 có ít nhất 3 nghiệm thuộc (-2; 2).

Mà phương trình bậc 3 có tối đa 3 nghiệm

Suy ra, phương trình 2t³ – 6t + 1 = 0 có đúng 3 nghiệm thuộc (-2; 2).

Vậy phương trình  có ít nhất 3 nghiệm thuộc (-7; 9).

Ví dụ 2: Chứng minh rằng phương trình (1 – m²)x⁵ – 3x – 1 = 0 luôn có nghiệm với mọi m.

Lời giải

Xét hàm số f(x) = (1 – m²)x⁵ – 3x – 1

Ta có: f(0) = – 1 và f(-1) = m² + 1 

nên f(−1).f(0) = −(m² + 1)  

Mặt khác: f(x) = (1 – m²)x⁵ – 3x – 1 là hàm đa thức nên liên tục trên [-1; 0] 

Suy ra, phương trình (1 – m²)x⁵ – 3x – 1 = 0 có ít nhất một nghiệm thuộc (-1; 0).

Vậy phương trình (1 – m²)x⁵ – 3x – 1 = 0 luôn có nghiệm với mọi m.

3. Bài tập tự luyện

Câu 1. Cho hàm số   

Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x = 4.

B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4.

C. Hàm số không liên tục tại x = 4.

D. Tất cả đều sai.

Câu 2. Cho hàm số   

Khẳng định nào sau đây đúng nhất: 

A. Hàm số liên tục tại x₀ = -1.                     

B. Hàm số liên tục tại mọi điểm.                 

C. Hàm số gián đoạn tại x₀ = -1.                 

D. Tất cả đều sai. 

Câu 3. Cho hàm số   

Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x₀ = 0.

B. Hàm số liên tục tại mọi điểm nhưng gián đoạn tại x₀ = 0.

C. Hàm số liên tục tại mọi điểm.

D. Tất cả đều sai.

Câu 4. Cho hàm số  Chọn câu đúng trong các câu sau:

(I) f(x) liên tục tại x = 2.

(II) f(x) gián đoạn tại x = 2.

(III) f(x) liên tục trên đoạn [-2; 2].

A. Chỉ (I) và (III).      B. Chỉ (I).                  C. Chỉ (II).                D. Chỉ (II) và (III).

Câu 5. Cho hàm số  Khẳng định nào sau đây đúng nhất.

A. Hàm số liên tục trên R.

B. Hàm số liên tục tại mọi R\{-2; 3} và hàm số gián đoạn tại x = -2; x = 3.

C. Hàm số liên tục tại x = -2; x = 3.

D. Tất cả đều sai.

Câu 6. Tìm m để các hàm số  liên tục trên .

A. m = 1                    B.                    C. m = 2                    D. m = 0

Câu 7. Tìm m để các hàm số  liên tục trên .

A. m = 1                    B.                   C. m = 2                    D. m = 0

Câu 8. Cho hàm số   . 

Tìm a để hàm số liên tục tại x₀ = 1.

 

Câu 9. Cho hàm số   

Giá trị của a để f(x) liên tục trên R là:

A. 1 hoặc 2.               B. 1 hoặc -1.              C. -1 hoặc 2.             D. 1 hoặc -2.

Câu 10. Cho hàm số  

Tìm khẳng định đúng trong các khẳng định sau: 

(I). f(x) liên tục tại  

(II). f(x) gián đoạn tại  

(III). f(x) liên tục trên R

A. Chỉ (I) và (II).                                         

B. Chỉ (II) và (III).

C. Chỉ (I) và (III).                                        

D. Cả (I),(II),(III) đều đúng.

Câu 11. Tìm khẳng định đúng trong các khẳng định sau:

I. f(x) liên tục trên đoạn [a; b] và f(a).f(b)

II. f(x) không liên tục trên [a; b] và f(a).f(b) ≥ 0 thì phương trình f(x) = 0 vô nghiệm.

A. Chỉ I đúng.           B. Chỉ II đúng.          C. Cả I và II đúng.     D. Cả I và II sai.

Câu 12. Cho phương trình 2x⁴ – 5x² + x + 1 = 0  (1) .Chọn khẳng định đúng trong các khẳng định sau:

A. Phương trình (1) không có nghiệm trong khoảng (-1; 1).          

B. Phương trình (1) không có nghiệm trong khoảng (-2; 0).          

C. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1).        

D. Phương trình (1) có ít nhất hai nghiệm trong khoảng (0; 2).

Câu 13. Số nghiệm thực của phương trình: 2x³ – 6x + 1 = 0 thuộc khoảng (- 2; 2) là:

A. 0.                          B. 1.                          C. 2.                          D. 3.

Câu 14. Cho phương trình x³ + ax² + bx + c = 0  (1) trong đó a, b, c là các tham số thực. Chọn khẳng định đúng trong các khẳng định sau:

A. Phương trình (1) vô nghiệm với mọi a, b, c.

B. Phương trình (1) có ít nhất một nghiệm với mọi a, b, c.

C. Phương trình (1) có ít nhất hai nghiệm với mọi a, b, c.

D. Phương trình (1) có ít nhất ba nghiệm với mọi a, b, c. 

Câu 15. Cho hàm số f(x) = x³ – 1000x² + 0,01. Phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây?

I. (-1; 0).                    II. (0; 1).                    III. (1; 2).

A. Chỉ I.                    B. Chỉ I và II.            C. Chỉ II.                   D. Chỉ III.

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
A	C	B	A	B	B	B	A	D	C	A	D	D	B	B

Phần 4: Cách tìm giới hạn của dãy số bằng định nghĩa cực hay

A. Phương pháp giải & Ví dụ

– Để chứng minh limu_n = 0 ta chứng minh với mọi số a > 0 nhỏ tùy ý luôn tồn tại một số n_a sao cho |u_n| n_a.

– Để chứng minh limu_n = 1 ta chứng minh lim(u_n-1) = 0.

– Để chứng minh limu_n = +∞ ta chứng minh với mọi số M > 0 lớn tùy ý, luôn tồn tại số tự nhiên n_M sao cho u_n > M ∀n > n_M.

– Để chứng minh limu_n = -∞ ta chứng minh lim(-u_n) = +∞

– Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.

Ví dụ minh họa

Bài 1: Chứng minh rằng:

Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

2. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 2: Chứng minh rằng dãy số (u_n ) : u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n = 1 ⇒ limu_2n = 1; u_(2n+1) = -1 ⇒ limu_(2n+1) = -1

Vì giới hạn của dãy số nếu có là duy nhất nên ta suy ra dãy (u_n) không có giới hạn.

Bài 3: Chứng minh các giới hạn sau:

Hướng dẫn:

1. Với mọi số thực dương M lớn tùy ý, ta có:

Ta chọn 

Do đó: 

2. Với mọi M > 0 lớn tùy ý, ta có:

Ta chọn 

Do đó: 

Bài 4: Chứng minh rằng:

Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

2. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

3. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 5: Chứng minh các giới hạn sau

Hướng dẫn:

1. Với mọi a > 0 nhỏ tùy ý, ta chọn 

2. Ta có

3. Với mọi số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 6: Dùng định nghĩa tìm các giới hạn sau :

Hướng dẫn:

1. Với số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có: 

Vậy A = 2

2. Với số thực a > 0 nhỏ tùy ý, ta chọn n_a thỏa mãn 

3. Với số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Vậy C = 1

Bài 7: Chứng minh rằng dãy số (u_n): u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n → +∞; u_(2n+1) = -(2n+1) → -∞

Do đó dãy số đã cho không có giới hạn.

Bài 8: Chứng minh các giới hạn sau:

Hướng dẫn:

1. Gọi m là số tự nhiên thỏa: m+1 > |a|. Khi đó với mọi n > m+1

Ta có:

Mà  Từ đó suy ra: 

2. Nếu a = 1 thì ta có đpcm

+ Giả sử a > 1. Khi đó:

+ 

Tóm lại ta luôn có:  với a > 0.

Phần 5: Cách tính tổng của cấp số nhân lùi vô hạn cực hay

A. Phương pháp giải & Ví dụ

Tổng của CSN lùi vô hạn

Cấp số nhân vô hạn u₁, u₂, u₃,..u_n,..có công bội q, với |q|

Tổng S của cấp số nhân đó là:

Ví dụ minh họa

Bài 1: Tìm tổng của cấp số nhân vô hạn sau:

Hướng dẫn:

Đây là tổng của cấp số nhân vô hạn có

 nên tổng là 

Bài 2: Tìm tổng của cấp số nhân lùi vô hạn (u_n) biết u_n = 1/(3ⁿ)

Hướng dẫn:

Vì

Bài 3: Tìm tổng của cấp số nhân vô hạn:

Hướng dẫn:

Vì các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = 1, q = -1/2

Vậy

Bài 4: Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3

Hướng dẫn:

Bài 5: Tìm tổng của dãy số sau:

Hướng dẫn:

Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = -1/10

Vậy

Bài 6: Tổng của một cấp số nhân lùi vô hạn là 5/3 tổng ba số hạng đầu tiên của nó là 39/25. Tìm số hạng đầu và công bội của cấp số đó.

Hướng dẫn:

Ta có

Bài 7: Cho dãy số (u_n) với . Tính tổng của dãy u_n

Hướng dẫn:

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Phần 6: Cách tính giới hạn của dãy số cực hay

A. Phương pháp giải & Ví dụ

– Ta quan sát, phân tích những đặc điểm của dãy số đề bài cho, từ đó rút ra công thu gọn cho tổng đó (có thể dùng công thức tính tổng của cấp số cộng hoặc cấp số nhân) hoặc biến đổi đại số để giảm bớt những hạng tử trong tổng,…

– Dùng các quy tắc tính giới hạn của dãy số để tính giới hạn của tổng đã cho sau khi đã thu gọn.

Ví dụ minh họa

Bài 1: Cho dãy số (u_n) với . Tính lim u_n

Hướng dẫn:

u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Do đó

Bài 2: Tính lim 

Hướng dẫn:

Vậy 

Bài 3: Tính 

Hướng dẫn:

Ta có

Mà

Vậy 

Bài 4: Tính 

Hướng dẫn:

Bài 5: Tính 

Hướng dẫn:

Bài 6: Cho dãy số (u_n). Biết  với mọi n ≥ 1. Tìm 

Hướng dẫn:

Bài 7: Tính 

Hướng dẫn:

Khi đó 

Phần 7: Cách tính giới hạn của dãy số có chứa căn thức cực hay, chi tiết

A. Phương pháp giải

+) Sử dụng các kiến thức sau:

• Với c là hằng số ta có: lim c = c, lim  = 0. Tổng quát lim  (k ≥ 1).

• Các phép toán trên các dãy có giới hạn hữu hạn

– Nếu lim u_n = a và lim v_n = b thì

  

– Nếu u_n ≥ 0 với mọi n và lim u_n = a thì

  

• Các phép toán trên dãy có giới hạn vô cực

  

+) Phương pháp giải:

a) Giới hạn dãy số dạng , trong đó f(n) và g(n) là các biểu thức chứa căn

=> Chia (các số hạng) của cả tử và mẫu cho lũy thừa của n có số mũ cao nhất trong dãy và dùng các kết quả trên để tính.

Quy ước:

Biểu thức  có bậc là 

Biểu thức  có bậc là 

b) Giới hạn dãy số dạng  với f(n) và g(n) là các đa thức

=> Rút lũy thừa của n có số mũ cao nhất ra và sử dụng kết quả của giới hạn dãy số tại vô cực để tính.

c) Giới hạn của dãy số dạng vô định () thì ta sử dụng các phép biến đổi liên hợp để đưa dãy số về dạng a) và b).

Các phép biến đổi liên hợp:

B. Ví dụ minh họa

Ví dụ 1: Tính giới hạn 

A. I = 1

B. I = – 1

C. I = 0

D. I = + ∞

Hướng dẫn giải:

Ta sử dụng phương pháp nhân với biểu thức liên hợp

Biểu thức liên hợp của biểu thức 

Đáp án B

Ví dụ 2: lim bằng:

A. + ∞

B. – ∞

C. -1

D. 0

Hướng dẫn giải:

Đáp án B

Ví dụ 3: Tính giới hạn: lim

A. – 1

B. 3

C. +∞

D. – ∞

Hướng dẫn giải:

Đáp án C

Ví dụ 4: Giới hạn lim bằng

A. – 1

B. 1

C. + ∞

D. – ∞

Hướng dẫn giải:

Ta tiến hành nhân chia với biểu thức liên hợp bậc ba của biểu thức 

Đáp án A

Ví dụ 5: Tính giới hạn lim

A. 

B. 0

C. + ∞

D. – ∞

Hướng dẫn giải:

Đáp án A

Giới hạn dãy số

A. Lý thuyết

I. Dãy số có giới hạn 0 .

1. Định nghĩa

Ta nói rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn 0 ( hay có giới hạn là 0 ) nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều có giá trị tuyệt đối nhỏ hơn số dương đó.

Kí hiệu: \(\lim {u_n} = 0\).

Nói một cách ngắn gọn, \(\lim {u_n} = 0\) nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ số hạng nào đó trở đi.

Từ định nghĩa suy ra rằng:

a) \(\lim {u_n} = 0 \Leftrightarrow \lim \left| {{u_n}} \right| = 0\).

b) Dãy số không đổi \(\left( {{u_n}} \right)\), với \({u_n} = 0\), có giới hạn là 0 .

c) Dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0 nếu \({u_n}\) có thể gần 0 bao nhiêu cũng được, miễn là \(n\) đủ lớn.

2. Một số dãy số có giới hạn 0

Định lí 4.1

Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\).

Nếu \(\left| {{u_n}} \right| \le {v_n}\) với mọi \(n\) và \(\lim {v_n} = 0\) thì \(\lim {u_n} = 0\).

Định lí 4.2

Nếu \(|q|

Người ta chúng mình được rằng

a) \(\lim \frac{1}{{\sqrt n }} = 0\).

b) \(\lim \frac{1}{{\sqrt[3]{n}}} = 0\)

c) \(\lim \frac{1}{{{n^k}}} = 0\) với mọi số nguyên dương \(k\) cho trước.

Trường hợp đặc biệt : \(\lim \frac{1}{n} = 0\).

d) \(\lim \frac{{{n^k}}}{{{a^n}}} = 0\) với mọi \(k \in \mathbb{N}*\) và mọi \(a > 1\) cho trước.

II. Dãy số có giới hạn hữu hạn.

1. Định nghĩa

Ta nói rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực L nếu \(\lim \left( {{u_n} – L} \right) = 0\).

Kí hiệu: \(\lim {u_n} = L\).

Dãy số có giới hạn là một số thực gọi là dãy số có giới hạn hữu hạn.

a) Dãy số không đổi \(\left( {{u_n}} \right)\) với \({u_n} = c\), có giới hạn là c.

b) \(\lim {u_n} = L\) khi và chỉ khi khoảng cách \(\left| {{u_n} – L} \right|\) trên trục số thực từ điểm \({u_n}\) đến L trở nên nhỏ bao nhiêu cũng được miễn là n đủ lớn; nói một cách hình ảnh, khi n tăng thì các điểm \({u_n}\) “ chụm lại” quanh điểm L.

c) Không phải mọi dãy số đều có giới hạn hữu hạn.

2. Một số định lí

Định lí 4.3

Giả sử \(\lim {u_n} = L\). Khi đó

a) \(\lim \left| {{u_n}} \right| = |L|\) và \(\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\).

b) Nếu \({u_n} \ge 0\) với mọi n thì \(L \ge 0\) và \(\lim \sqrt {{u_n}}  = \sqrt L \).

Định lí 4.4

Giả sử \(\lim {u_n} = L,\lim {v_n} = M\) và c là một hằng số. Khi đó

a) \(\lim \left( {{u_n} + {v_n}} \right) = L + M\).

b) \(\lim \left( {{u_n} – {v_n}} \right) = L – M\).

c) \(\lim \left( {{u_n}{v_n}} \right) = LM\).

D) \(\lim \left( {c{u_n}} \right) = cL\).

e) \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{L}{M}(\) nếu \(M \ne 0)\).

3. Tổng của cấp số nhân lùi vô hạn

Định nghĩa

Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa \(|q|

Công thức tính tổng của cấp số nhân lùi vô hạn:

\(S = {u_1} + {u_1}q + {u_1}{q^2} +  \ldots  = \frac{{{u_1}}}{{1 – q}}\)

III. Dãy số có giới hạn vô cực.

1. Dãy số có giới hạn \( + \infty \)

Ta nói rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn \( + \infty \) nếu với mỗi số dương tùy ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều lớn hơn số dương đó.

Kí hiệu: \(\lim {u_n} =  + \infty \).

Nói một cách ngắn gọn, \(\lim {u_n} =  + \infty \) nếu \({u_n}\) có thể lớn hơn một số dương lớn tùy ý, kể từ số hạng nào đó trở đi.

Người ta chứng minh được rằng:

a) \(\lim \sqrt {{u_n}}  =  + \infty \).

b) \(\lim \sqrt[3]{{{u_n}}} =  + \infty \)

c) \(\lim {n^k} =  + \infty \) với một số nguyên dương \(k\) cho trước.

Trường hợp đặc biệt : \(\lim n =  + \infty \).

d) \(\lim {q^n} =  + \infty \) nếu \(q > 1\).

2. Dãy số có giới hạn \( – \infty \)

Ta nói rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn \( – \infty \) nếu với mỗi số âm tùy ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều nhỏ hơn số âm đó.

Kí hiệu: \(\lim {u_n} =  – \infty \).

Nói một cách ngắn gọn, \(\lim {u_n} =  – \infty \) nếu \({u_n}\) có thể nhỏ hơn một số âm nhỏ tùy ý, kể từ số hạng nào đó trở đi.

Nhận xét:

a) \(\lim {u_n} =  – \infty  \Leftrightarrow \lim \left( { – {u_n}} \right) =  + \infty \).

b) Nếu \(\lim \left| {{u_n}} \right| =  + \infty \) thì \(\left| {{u_n}} \right|\) trở nên lớn bao nhiêu cũng được miễn n đủ lớn. Đo đó \(\left| {\frac{1}{{{u_n}}}} \right| = \frac{1}{{\left| {{u_n}} \right|}}\) trở nên nhỏ bao nhiêu cũng được, miễn n đủ lớn. Nói cách khác, nếu \(\lim \left| {{u_n}} \right| =  + \infty \) thì \(\lim \frac{1}{{{u_n}}} = 0\).

Định lí 4.5

Nếu \(\lim \left| {{u_n}} \right| =  + \infty \) thì \(\lim \frac{1}{{{u_n}}} = 0\).

3. Một vài quy tắc tìm giới hạn vô cực

Quy tắc 1

Nếu \(\lim {u_n} =  \pm \infty \) và \(\lim {{\rm{v}}_n} =  \pm \infty \) thì \(\lim \left( {{u_n}{v_n}} \right)\) được cho trong bảng sau:

Quy tắc 2

Nếu \(\lim {u_n} =  \pm \infty \) và \(\lim {{\rm{v}}_n} = L \ne 0\) thì \(\lim \left( {{u_n}{v_n}} \right)\) được cho trong bảng sau:

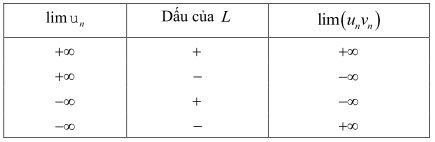
Quy tắc 3

Nếu \(\lim {u_n} = L \ne 0\) và \(\lim {{\rm{v}}_n} = 0\) và \({v_n} > 0\) hoặc \({v_n}

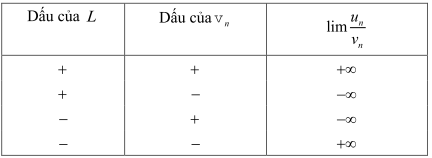
B. Các dạng toán về giới hạn dãy số

Dạng 1. Tính giới hạn dãy số cho bởi công thức

Câu 1: \(\lim \left( {{n^3} – 2n + 1} \right)\) bằng

A. 0 .

B. 1 .

C. \( – \infty \).

D. \( + \infty \).

Đáp án D.

Lời giải

Ta có: \({n^3} – 2n + 1 = {n^3}\left( {1 – \frac{2}{{{n^2}}} + \frac{1}{{{n^3}}}} \right)\).

Vì \(\lim {n^3} =  + \infty \) và \(\lim \left( {1 – \frac{2}{{{n^2}}} + \frac{1}{{{n^3}}}} \right) = 1 > 0\)

 nên theo quy tắc \(2,\lim \left( {{n^3} – 2n + 1} \right) =  + \infty \)

Câu 2: \(\lim \left( {5n – {n^2} + 1} \right)\) bằng

A. \( + \infty \).

B. \( – \infty \).

C. 5 .

D. \( – 1\).

Chọn B.

Hướng dẫn giải

Ta có \(5n – {n^2} + 1 = {n^2}\left( { – 1 + \frac{5}{n} + \frac{1}{{{n^2}}}} \right)\).

Vì \(\lim {n^2} =  + \infty \) và \(\lim \left( { – 1 + \frac{5}{n} + \frac{1}{{{n^2}}}} \right) =  – 1

nên \(\lim \left( {5n – {n^2} + 1} \right) =  – \infty \) (theo quy tắc 2 ).

Câu 3: \(\lim {u_n}\), với \({u_n} = \frac{{5{n^2} + 3n – 7}}{{{n^2}}}\) bằng:

A. 0 .

B. 5 .

C. 3 .

D. \( – 7\).

Chọn B.

Hướng dẫn giải

Ta có:

\(\begin{array}{l}\lim {u_n} = \lim \left( {\frac{{5{n^2}}}{{{n^2}}} + \frac{{3n}}{{{n^2}}} – \frac{7}{{{n^2}}}} \right)\\ = \lim \left( {5 + \frac{3}{n} – \frac{7}{{{n^2}}}} \right) = 5\end{array}\).

Câu 4: \(\quad \lim {u_n}\), với \({u_n} = \frac{{2{n^3} – 3{n^2} + n + 5}}{{{n^3} – {n^2} + 7}}\) bằng

A. \( – 3\).

B. 1 .

C. 2 .

D. 0 .

Chọn C.

Hướng dẫn giải

Chia cả tử và mẫu của phân thức cho \({n^3}\) ( \({n^3}\) là lũy thừa bậc cao nhất của n trong phân thức), ta được: \({u_n} = \frac{{2 – \frac{3}{n} + \frac{1}{{{n^2}}} + \frac{5}{{{n^3}}}}}{{1 – \frac{1}{n} + \frac{7}{{{n^3}}}}}\).

Vì \(\lim \left( {2 – \frac{3}{n} + \frac{1}{{{n^2}}} + \frac{5}{{{n^3}}}} \right) = 2\) và

 \(\lim \left( {1 – \frac{1}{n} + \frac{7}{{{n^3}}}} \right) = 1 \ne 0\)

nên \(\lim \frac{{2{n^3} – 3{n^2} + n + 5}}{{{n^3} – {n^2} + 7}} = \frac{2}{1} = 2.\)

Ví dụ 5: Giới hạn của dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \frac{{{n^3} + 2n + 1}}{{{n^4} + 3{n^3} + 5{n^2} + 6}}\) bằng

A. 1 .

B. 0 .

C. \( + \infty \).

D. \(\frac{1}{3}\).

Hướng dẫn giải

Chọn B.

Chia cả tử và mẫu của phân thức cho \({n^4}\) ( \({n^4}\) là bậc cao nhất của n trong phân thức), ta được

\(\begin{array}{l}\lim {u_n} = \lim \frac{{{n^3} + 2n + 1}}{{{n^4} + 3{n^3} + 5{n^2} + 6}}\\ = \lim \frac{{\frac{1}{n} + \frac{2}{{{n^3}}} + \frac{1}{{{n^4}}}}}{{1 + \frac{3}{n} + \frac{5}{{{n^2}}} + \frac{6}{{{n^3}}}}} = \frac{0}{1} = 0.\end{array}\)

Ví dụ 6: Giới hạn của dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{3{n^3} + 2n – 1}}{{2{n^2} – n}}\), bằng

A. \(\frac{3}{2}\).

B. 0 .

C. \( + \infty \).

D. 1 .

Chọn C.

Hướng dẫn giải

Chia cả tử và mẫu cho \({n^2}\) ( \({n^2}\) là lũy thừa bậc cao nhất của n trong mẫu thức ), ta được \({u_n} = \frac{{3{n^3} + 2n – 1}}{{2{n^2} – n}} = \frac{{3n + \frac{2}{n} – \frac{1}{{{n^2}}}}}{{2 – \frac{1}{n}}}\).

Vậy \(\lim {u_n} = \lim \left( {\frac{{3n}}{2}} \right) =  + \infty \).

Ví dụ 7: \(\lim \frac{{\sin (n!)}}{{{n^2} + 1}}\) bằng

A. 0 .

B. 1 .

C. \( + \infty \).

D. 2 .

Chọn A.

Hướng dẫn giải

Ta có \(\left| {\frac{{\sin (n!)}}{{{n^2} + 1}}} \right| \le \frac{1}{{{n^2} + 1}}\) mà \(\lim \frac{1}{{{n^2} + 1}} = 0\) nên chọn đáp án \({\bf{A}}\).

Ví dụ 8: \(\lim \frac{{{{( – 1)}^n}}}{{n(n + 1)}}\) bằng

A. \( – 1\).

B. 1 .

C. \( + \infty \).

D. 0 .

Chon D.

Hướng dẫn giải

Ta có \(\left| {\frac{{{{( – 1)}^n}}}{{n(n + 1)}}} \right| = \frac{1}{{n(n + 1)}}

 mà \(\lim \frac{1}{{{n^2}}} = 0\) nên suy ra \(\lim \frac{{{{( – 1)}^n}}}{{n(n + 1)}} = 0\)

Ví dụ 9: Tính giới hạn \(I = \lim \left( {\sqrt {{n^2} – 2n + 3}  – n} \right)\)

A. \(I = 1\).

B. \(I =  – 1\).

C. \(I = 0\).

D. \(I =  + \infty \).

Chọn B.

Hướng dẫn giải

Ta có

\(\begin{array}{l}I = \lim \left( {\sqrt {{n^2} – 2n + 3}  – n} \right)\\ = \lim \frac{{\left( {\sqrt {{n^2} – 2n + 3}  – n} \right)\left( {\sqrt {{n^2} – 2n + 3}  + n} \right)}}{{\sqrt {{n^2} – 2n + 3}  + n}}\end{array}\)

\(\begin{array}{l} = \lim \frac{{\left( {{n^2} – 2n + 3} \right) – {n^2}}}{{\sqrt {{n^2} – 2n + 3}  + n}}\\ = \lim \frac{{ – 2n + 3}}{{\sqrt {{n^2} – 2n + 3}  + n}}\\ = \lim \frac{{ – 2 + \frac{3}{n}}}{{\sqrt {1 – \frac{2}{n} + \frac{3}{{{n^2}}}}  + 1}}\\ = \frac{{ – 2}}{{\sqrt 1  + 1}} =  – 1\end{array}\).

Ví dụ 10: \(\lim \left( {n – \sqrt[3]{{8{n^3} + 3n + 2}}} \right)\) bằng:

A. \( + \infty \).

B. \( – \infty \).

C. \( – 1\).

D. 0 .

Chọn B.

Hướng dẫn giải

Ta có \(\lim \left( {n – \sqrt[3]{{8{n^3} + 3n + 2}}} \right) = \lim n\left( {1 – \sqrt[3]{{8 + \frac{3}{{{n^2}}} + \frac{2}{{{n^3}}}}}} \right)\).

Vì \(\lim n =  + \infty ,\lim \left( {1 – \sqrt[3]{{8 + \frac{3}{{{n^2}}} + \frac{2}{{{n^3}}}}}} \right) = 1 – \sqrt[3]{8} =  – 1

nên \(\lim \left( {n – \sqrt[3]{{8{n^3} + 3n + 2}}} \right) =  – \infty \).