50 Bài tập Nhị thức Niu-tơn (có đáp án)- Toán 11

Bài tập Toán 11 Chương 2 Bài 3: Nhị thức Niu – Tơn

A. Bài tập Nhị thức Niu-tơn

I. Bài tập trắc nghiệm

Bài 1: Tìm số hạng đứng giữa trong khai triển (x³ + xy)²¹

Lời giải:

Theo khai triển nhị thức Niu-tơn, ta có

Suy ra khai triển (x³ + xy)²¹ có 22 số hạng nên có hai số hạng đứng giữa là số hạng thứ 11 (ứng với k = 10) và số hạng thứ 12 (ứng với k = 11). Vậy hai số hạng đứng giữa cần tìm là

Chọn đáp án D

Bài 2: Tìm hệ số của x⁵ trong khai triển P(x) = x(1 – 2x)⁵ + x²(1 + 3x)¹⁰

A. 80

B. 3240

C. 3320

D. 259200

Lời giải:

Chọn đáp án C

Bài 3: Tìm hệ số của x⁵ trong khai triển : P(x) = (1 + x) + 2(1 + x)² + … + 8(1 + x⁾⁸.

A. 630

B. 635

C. 636

D.637

Lời giải:

Các biểu thức (1 + x), (1 + x)², ⋯, (1 + x)⁴ không chứa số hạng chứa x⁵.

Chọn đáp án C

Bài 4: Tìm số nguyên dương n thỏa mãn .

A.n = 8

B.n = 9

C.n = 10

D. n = 11

Lời giải:

Chọn đáp án C

Bài 5: Tìm số nguyên dương n thỏa mãn .

A.n = 5

B.n = 9

C.n = 10

D.n = 4

Lời giải:

Chọn đáp án A

Bài 6: Tìm số nguyên dương n sao cho: 

A. 5

B. 11

C. 12

D. 4

Lời giải:

Chọn đáp án A

Bài 7: Tính 

Lời giải:

Chọn đáp án D

Bài 8: Khai triển biểu thức (x-m²)⁴ thành tổng các đơn thức:

A. x⁴ –x³m+x²m² + m⁴

B. x⁴ –x³m²+x²m⁴ –xm⁶+ m⁸

C. x⁴ –4x³m+6x²m² -4xm+ m⁴

D. x⁴ –4x³m²+6x²m⁴ – 4xm⁶+ m⁸

Lời giải:

Sử dụng nhị thức Niuton với a = x, b = – m²

Chọn đáp án D

Bài 9: Tìm số hạng không chứa x trong khai triển

A. 2268      

B. -2268

C. 84      

D. -27

Lời giải:

Chọn đáp án là B

Bài 10: Xác định hệ số của số hạng chứa x3 trong khai triển (x²–$\frac{x}{2}$)n nếu biết tổng các hệ số của ba số hạng đầu trong khai triển đó bằng 49.

A. 160      

B. -160

C. 160x³      

D. -160x³

Lời giải:

Chọn đáp án là B

II. Bài tập tự luận có lời giải

Bài 1: Tính tổng S = 3²⁰¹⁵.$C_{2015}^0$-3²⁰¹⁴$C_{2015}^1$+3²⁰¹³$C_{2015}^2$-…+3$C_{2015}^{2014}$ –$C_{2015}^{2015}$?

Lời giải:

Bài 2: Trong khai triển nhị thức (a + 2)^{n + 6}, (n ∈ N). Có tất cả 17 số hạng. Vậy n bằng:

Lời giải:

Bài 3: Tìm hệ số của x¹² trong khai triển (2x – x²)¹⁰

Lời giải:

Bài 4: Tìm số hạng chứa x³ trong khai triển 

Lời giải:

Bài 5: Viết khai triển theo công thức nhị thức Niu – Tơn:

a) (a + 2b)⁵                  

b) (a – $\sqrt{2}$)⁶                  

c) (x – $\frac{1}{x}$)¹³

Lời giải:

a) Theo dòng 5 của tam giác Pascal, ta có:

(a + 2b)⁵ = a⁵ + 5a⁴(2b) + 10a³(2b)² + 10a²(2b)³ + 5a(2b)⁴ + (2b)⁵
= a⁵ + 10a⁴b + 40a³b² + 80a²b³ + 80ab⁴ + 32b⁵

b) Theo dòng 6 của tam giác Pascal, ta có:

(a – $\sqrt{2}$)⁶ = [a + (-$\sqrt{2}$)]⁶ = a⁶ + 6a⁵ (-$\sqrt{2}$) + 15a⁴ (-$\sqrt{2}$)² + 20a³ (-$\sqrt{2}$)³ + 15a² (-$\sqrt{2}$)⁴ + 6a(-$\sqrt{2}$)⁵ + (-$\sqrt{2}$)⁶ = a⁶ – 6$\sqrt{2}$a⁵ + 30a⁴ – 40$\sqrt{2}$a³ + 60a² – 24$\sqrt{2}$a + 8.

c) Theo công thức nhị thức Niu – Tơn, ta có:

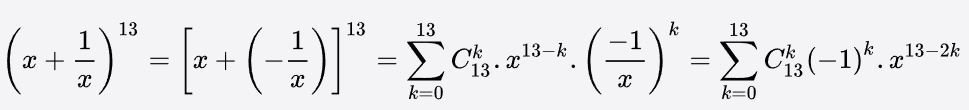
Nhận xét: Trong trường hợp số mũ n khá nhỏ (chẳng hạn trong các câu a) và b) trên đây) thì ta có thể sử dụng tam giác Pascal để tính nhanh các hệ số của khai triển.

Bài 6 Tìm hệ số của x3 trong khai triển của biểu thức: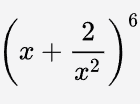

Lời giải:

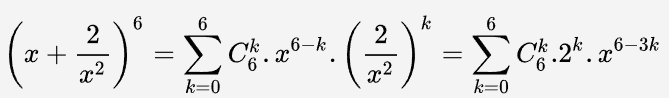
Trong tổng này, số hạng Ck⁶ . 2k . x⁶ – 3k có số mũ của x bằng 3 khi và chỉ khi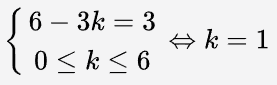

Do đó hệ số của x3 trong khai triển của biểu thức đã cho là:  = 2 . 6 = 12

Bài 7: Tìm hệ số của x⁵ trong khai triển : P(x) = (1 + x) + 2(1 + x)² + … + 8(1 + x)⁸.

Lời giải:

Các biểu thức (1 + x), (1 + x)², ⋯, (1 + x)⁴ không chứa số hạng chứa x⁵.

Bài 8 Tìm số nguyên dương n thỏa mãn 

Lời giải:

Bài 9 Tính 

Lời giải:

Bài 10 Tìm số hạng không chứa x trong khai triển

Lời giải:

III. Bài tập vận dụng

Bài 1 Biết hệ số của x²  trong khai triển của (1 – 3x)ⁿ là 90. Tìm n.

Bài 2 Tìm số hạng không chứa x trong khai triển của (x³ + )⁸

Bài 3 Từ khai triển biểu thức (3x – 4)¹⁷ thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.

Bài 4 Chứng minh rằng:
a) 11¹⁰ – 1 chia hết cho 100;

b) 101¹⁰⁰– 1 chia hết cho 10 000;

c) $\sqrt{10}[(1+\sqrt{10})100–(1-\sqrt{10})100]$ là một số nguyên

Bài 5 Viết khai triển theo công thức nhị thức Niu – Tơn:

a) (a + 2b)⁵                                   

b) (a – $\sqrt{2}$)⁶                                   

c) (x – $\frac{1}{x}$)¹³

Bài 6 Tìm hệ số của x³ trong khai triển của biểu thức:

Bài 7 Biết hệ số của x² trong khai triển của (1 – 3x)ⁿ là 90. Tìm n.

Bài 8 Tìm số hạng không chứa x trong khai triển của (x³ + $\frac{1}{x}$)⁸

Bài 9 Từ khai triển biểu thức (3x – 4)¹⁷ thành đa thức, hãy tính tổng các hệ số của đa thức nhận được?

Bài 10 Chứng minh rằng:

a) 11¹⁰ – 1 chia hết cho 100;

b) 101¹⁰⁰ – 1 chia hết cho 10 000;

c)  là một số nguyên.

A. Lý thuyết Nhị thức Niu-tơn

I. Công thức nhị thức Niu- tơn

Ta có:

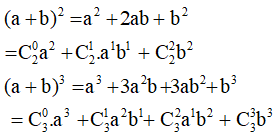
– Công thức nhị thức Niu – tơn.

${(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b+\text{\hspace{0.17em}}\mathrm{\dots }+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{\dots .}+\text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n$

– Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{\dots }\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{\dots }$$+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{\dots }\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

– Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

– Ví dụ 1. Khai triển biểu thức: (a – b)⁵.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

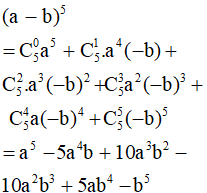
– Ví dụ 2. Khai triển biểu thức: (3x – 2)⁴.

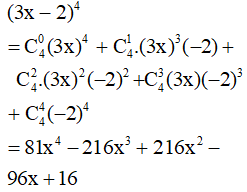
II. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

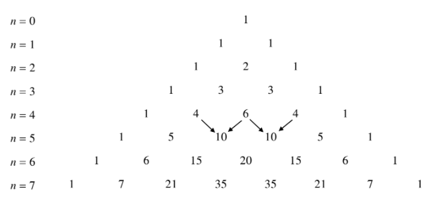
– Nhận xét:

Từ công thức $C_n^k=C_{n-1}^{k-1}+C_{n-1}^k$ suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. $C_6^2=C_5^1+C_5^2=5+10=15$.