Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Thủ thuật giải trắc nghiệm lượng giác bằng máy tính Casio
Phần 1: Lý thuyết + biến đổi lương giác
Bài 1 : Chọn đáp án đúng khi rút gọn các biểu thức sau
Ví dụ mẫu: Rút gọn
\(P = \frac{{{{\sin }^4}x + \sin 2x – {{\cos }^4}x}}{{\tan 2x – 1}}\)
Nhập \(\frac{{{{\sin }^4}x + \sin 2x – {{\cos }^4}x}}{{\tan 2x – 1}}\) Calc: \({\rm{x}} = 60 \Rightarrow {\rm{P}} = – \frac{1}{2} = \cos 120 = \cos 2{\rm{x}}\)
Ví dụ 2: \(P = \frac{{{{\cos }^3}x – \cos 3x}}{{\cos x}} + \frac{{{{\sin }^3}x + \sin 3x}}{{\sin x}}\)
Nhập \(\frac{{{{\cos }^3}x – \cos 3x}}{{\cos x}} + \frac{{{{\sin }^3}x + \sin 3x}}{{\sin x}}\)
Calc: \({\rm{x}} = 60 \Rightarrow {\rm{P}} = 3;\) Calc \(:{\rm{x}} = 15 \Rightarrow {\rm{P}} = 3 \ldots \)
Vậy \(P = 3\)
Ví dụ 3 .Tập xác định của hàm số \(y = \frac{1}{{2\sin x – \sqrt 3 }}\) là
A. \(D = R\backslash \left\{ {\frac{\pi }{3} + 2k\pi ;k \in z} \right\}\)
B. \(\left. {D = R\backslash \frac{\pi }{6} + 2k\pi ;k \in z} \right\}\)
C. \(D = R\backslash \left\{ {\frac{\pi }{6} + 2k\pi ,\frac{{5\pi }}{6} + 2k\pi ;k \in z} \right\}\quad \)
D. \(D = R\backslash \left\{ {\frac{\pi }{3} + 2k\pi ,\frac{{2\pi }}{3} + 2k\pi ;k \in z} \right\}\)
Nhập Mode \(7f(x) = \frac{1}{{2\sin x – \sqrt 3 }}\)
Start : 0 ; End 180 ; Step 15 ta có bảng
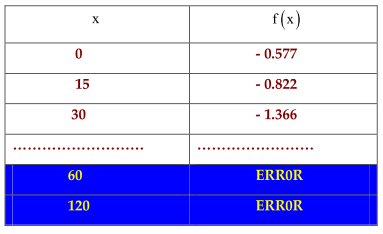
Vậy đáp án là \({\rm{D}}\)
Ví dụ Hàm số \({\rm{y}} = 4\sin {\rm{x}} + \cos 2{\rm{x}}\) có bao nhiêu cực trị thuộc \((0;2\pi )\)
Có \({{\rm{y}}^\prime } = 4\cos {\rm{x}} – 2\sin 2{\rm{x}}\)
Nhập Mode7 \({\rm{f}}({\rm{x}}) = 4\cos {\rm{x}} – 2\sin 2{\rm{x}}\) Start :0; End : 180;Step : 15 và \({\rm{f}}({\rm{x}}) = 4\cos {\rm{x}} – 2\sin 2{\rm{x}}\)
Thấy đổi dấu 2 lần tại \({\rm{x}} = 90 \vee {\rm{x}} = 270\) nên hàm số có 2 cực trị
Ví dụ : tìm Max – Min hàm số
1. \(y = \sqrt 2 \cos 2x + 4\sin x\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\)
Có \({y^\prime } = – 2\sqrt 2 \sin 2x + 4\cos x\)
Nhập Mode \(7f(x) = – 2\sqrt 2 \sin 2x + 4\cos x\)
Start : 0 ; End :90 ; Step 15 ta có
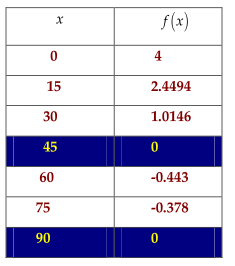
Vậy nghiệm là \[x = \frac{\pi }{4};x = \frac{\pi }{2}\]
Nhập \(f(x) = \sqrt 2 \cos 2x + 4\sin x\) Calc : \({\bf{x}} = 0\)
\( \to f(0) = \sqrt 2 ;\) Calc \(:x = 45 \to f(45) = 2\sqrt 2 ;\)
Calc \(:x = 90 \to f(x) = 4 – \sqrt 2 \)
Chú ý : Có thể nhập Mode \(7f(x) = \sqrt 2 \cos 2x + 4\sin x\) đề tìm Max, Min nhưng
sẽ phải khảo sát table nhiều lân vì kho thể lấy bước nhẩy quá lớn do đó sẽ lâu hơn cách trên
Ví dụ giải các phương trình
Bài 1. Giải phương trình
\(\cos 3{\rm{x}} – 4\cos 2{\rm{x}} + 3\cos {\rm{x}} – 4 = 0\quad (*),\forall {\rm{x}} \in [0;14]\)
Lời giải
Bước 1: Nhập vào Casio
Mode7, máy hiện thị
\(f(x) = \mathop \to \limits^{{\rm{ nhap }}} f(x) = \cos 3x – 4\cos 2x + 3\cos x – 4\)
Start : \(x = 0\)
End : \(x = 180\)
Step : 15
Ta có kết quả \(x = 90 = \frac{\pi }{2}\)
Làm tương tự
\(f(x) = \mathop \to \limits^{{\rm{ nhap }}} f(x) = \cos 3x – 4\cos 2x + 3\cos x – 4\)
Start : \(x = 180\)
End : \(x = 360\)
Step : 15
Ta có kết quả \(x = 270 = \frac{{3\pi }}{2}\)
Hết nghiệm , biểu diễn nhanh trên vòng tròn lượng giác ta có
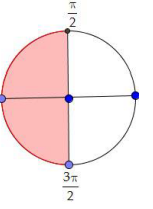
Hai nghiệm đối xứng nhau qua gốc tọa độ Do đó chỉ nhận nghiệm \(x = \frac{\pi }{2} + k\pi ,k \in Z\)
Bước 2: Do bài chỉ yêu cầu tìm trên [0 ; 14] nên ta làm tiếp như sau
Cho \(0 \le x = \frac{\pi }{2} + k\pi ,k \in Z \le 14 \Leftrightarrow 0 \le 0.5 + k \le \frac{{14}}{\pi } \approx 4.46\)
Nhập mode7, \(f(x) = 0.5 + x;\) cho \(:\left\{ {\begin{array}{*{20}{l}}{{\rm{ Start }}: – 3}\\{{\rm{ End }}:3\quad \mathop \to \limits^{{\rm{ tim}}{\rm{.duoc }}} k = \{ 0;1;2;3\} }\\{{\rm{ Step }}:1}\end{array}} \right.\)
Vậy phương trình có 4 nghiệm \(x = \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{5\pi }}{2};\frac{{7\pi }}{2}} \right\}\)
Bài 2. Giải phương trình: \((2\cos x – 1)(2\sin x + \cos x) = \sin 2x – \sin x\quad (*)\) \(f(x) = \mathop \to \limits^{{\rm{ nhap }}} f(x) = (2\cos x – 1)(2\sin x + \cos x) – \sin 2x + \sin x\)
Start: \(x = 0\)
End: \(x = 180\)
Step : 15
Ta có kết quả \(x = 60 = \frac{\pi }{3};x = 135 = \frac{{3\pi }}{4}\)
Lần 2
\(f(x) = \mathop \to \limits^{{\rm{ nhap }}} f(x) = (2\cos x – 1)(2\sin x + \cos x) – \sin 2x + \sin x\)
Start: \(x = 180\)
End : \(x = 360\)
Step : 15
Ta có kết quả
\(x = 300 = – \frac{\pi }{3};x = 315 = – \frac{\pi }{4}\)
Kết hợp trên đường tròn ta có
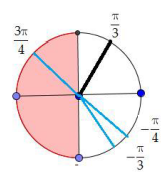
Các nghiệm là
\(\left[ {\begin{array}{*{20}{l}}{x = \pm \frac{\pi }{3} + k2\pi }\\{x = – \frac{\pi }{4} + k\pi }\end{array}} \right.\)
Chú ý: các điểm đứng một mình \( + k2\pi \)
Có 2 điểm đối xứng \(\quad + k\pi \)
4 điểm cách đều nhau \( + \frac{{k\pi }}{2}\)
Tổng quát : nếu có n điểm cách đều ta \( + \frac{{2k\pi }}{n}\)
Bài 3. Giải phương trình\({\rm{ }}\cos 3x + \cos 2x – \cos x – 1 = 0\quad (*)\)
Hướng dẫn giải
\(f(x) = \cos 3x + \cos 2x – \cos x – 1\)
Start: \(x = 0\)
End : \(x = 180\)
Step : 15
Kết quá
\(x = 0 = k2\pi ;x = 120 = \frac{{2\pi }}{3},x = 180 = \pi \)
\(f(x) = \cos 3x + \cos 2x – \cos x – 1\)
Start: \(x = 0\)
Lân 2 End: \(x = 180\)
Step : 15
Kết quả \(x = 240 = – \frac{{2\pi }}{3};x = 360 = 2\pi \equiv 0\),
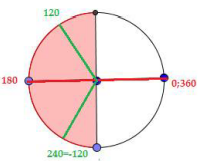
Vậy
\(\left[ {\begin{array}{*{20}{l}}{x = k\pi }\\{x = \pm \frac{{2\pi }}{3} + k2\pi }\end{array}} \right.\)
Bài 4. Giải phương trình: \(\sin {\rm{x}} + \cos {\rm{x}} + 1 + \sin 2{\rm{x}} + \cos 2{\rm{x}} = 0\quad (*)\)
Hướng dẫn giải \(f(x) = \sin x + \cos x + 1 + \sin 2x + \cos 2x\)
Start: \(x = 0\)
End: \(x = 180\)
cho
\(x = 120 = \frac{{2\pi }}{3},x = 135 = \frac{{3\pi }}{4}\)
Step : 15
Lần 2
\(f(x) = \sin x + \cos x + 1 + \sin 2x + \cos 2x\)
Start: \(x = 180\)
End: \(x = 360\)
cho
\(x = 240 = – \frac{{2\pi }}{3},x = 315 = – \frac{\pi }{4}\)
Step : 15
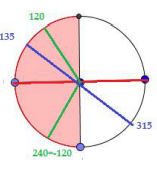
Kết quả\(\left[ {\begin{array}{*{20}{l}}{x = – \frac{\pi }{4} + k\pi }\\{x = \pm \frac{{2\pi }}{3} + k2\pi }\end{array}} \right.\)
1. \(P = {\sin ^4}x + {\sin ^2}x{\cos ^2}x\)
Nhập \(P = {\sin ^4}x + {\sin ^2}x{\cos ^2}x – {\sin ^2}x\) rồi
Calc : \(x = 60 \Rightarrow {\rm{P}} = 0;\) Calc \(:{\rm{x}} = 45;{\rm{P}} = 0 \ldots \) vậy đáp án là \({\rm{A}}\)
A. \({\sin ^2}x\)
B. \({\cos ^2}x\)
C. \(\cos 2x\)
D. \(\sin 2x\)
Xem thêm