Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Bài giảng Toán học 12 Bài 2: Cực trị của hàm số
CỰC TRỊ CÓ THAM SỐ
I. Phương pháp giải
Điều kiện cần để hàm số có cực trị.
Giả sử hàm số f đạt cực trị tại điểm \[{x_0}\].
Khi đó, nếu f có đạo hàm tại \[{x_0}\] thì \[f’\left( {{x_0}} \right) = 0\].
Điều kiện đủ để hàm số có cực trị: có hai dấu hiệu:
– Cho \[y = f\left( x \right)\] liên tục trên khoảng (a;b) chứa \[{x_0}\], có đạo hàm trên các khoảng \[\left( {a;{x_0}} \right)\] và \[\left( {{x_0};b} \right)\]:
Nếu \[f’\left( x \right)\] đổi dấu từ âm sang dương thì f đạt cực tiểu tại \[{x_0}\]
Nếu \[f’\left( x \right)\] đổi dấu từ dương sang âm thì f đạt cực đại tại \[{x_0}\].
– Cho \[y = f\left( x \right)\] có đạo hàm cấp hai trên khoảng (a;b) chứa \[{x_0}\]:
Nếu \[f’\left( {{x_0}} \right) = 0\] và \[f”\left( {{x_0}} \right) > 0\] thì f đạt cực tiểu tại \[{x_0}\]
Nếu \[f’\left( {{x_0}} \right) = 0\] và \[f”\left( {{x_0}} \right) < 0\] thì f đạt cực đại tại \[{x_0}\]
Chú ý:
1) Hàm số f có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp D, nhưng không đạt tại các biên.
2) Tung độ cực trị \[y = f\left( x \right)\] tại \[x = {x_0}\] có 3 hướn tính:
Hàm số bất kỳ: dùng phép thế \[{y_0} = f\left( {{x_0}} \right)\]
Hàm đa thức: chia đạo hàm \[y = q\left( x \right).y’ + r\left( x \right) \Rightarrow {y_0} = r\left( {{x_0}} \right)\]
Hàm hữu tỉ: đạo hàm riêng tử, riêng mẫu
\[y = f\left( x \right) = \frac{{u\left( x \right)}}{{v\left( x \right)}}\] thì \[{y_0} = \frac{{u\left( {{x_0}} \right)}}{{v\left( {{x_0}} \right)}} = \frac{{u’\left( {{x_0}} \right)}}{{v’\left( {{x_0}} \right)}}\]
Đặc biệt: Với hàm bậc 3 có CĐ, CT và nếu \[y = f\left( x \right) = q\left( x \right).y’ + r\left( x \right)\] thì phương trình đường thẳng qua CĐ, CT là \[y = r\left( x \right)\].
II. Ví dụ minh họa
Bài toán 1. Tìm m để hàm số:
\[y = – \left( {{m^2} + 5m} \right){x^3} + 6m{x^2} + 6x – 5\] đạt cực đại tại \[x = 1\].
Giải
\[D = \mathbb{R}\]. Ta có \[y’ = – 3\left( {{m^2} + 5m} \right){x^2} + 12mx + 6\]
Nếu hàm số đạt cực đại tại \[x = 1\] thì \[y’\left( 1 \right) = 0\]
\[ – 3{m^2} – 3m + 6 = 0 \Leftrightarrow m = 1\] hoặc \[m = – 2\].
Ta có \[y” = – 6\left( {{m^2} + 5m} \right)x + 12m\]
Thử lại:
Với \[m = 1\] thì \[y” = – 36x + 12\] nên \[y”\left( 1 \right) = – 24 < 0\], hàm số đạt cực đại tại \[x = 1\].
Với \[m = – 2\] thì \[y” = 36x – 24\] nên \[y”\left( 1 \right) = 12 > 0\], hàm số đạt cực tiểu tại \[x = 1\] (loại).
Vậy với \[m = 1\] thì hàm số đạt cực đại tại \[x = 1\].
Bài toán 2. Tìm m để hàm số: \[y = \frac{{{x^2} + \left( {1 – m} \right)x – 2}}{{x + m}}\] đạt cực tiểu tại \[x = 0\].
Giải
\[D = \mathbb{R}\backslash \left\{ { – m} \right\}\]. Ta có \[y’ = \frac{{{x^2} + 2mx – {m^2} + m + 2}}{{{{\left( {x + m} \right)}^2}}}\]
Nếu hàm số đạt cực tiểu tại \[x = 0\] thì
\[y’\left( 0 \right) = 0 \Rightarrow – {m^2} + m + 2 = 0 \Rightarrow m = – 1\] hoặc \[m = 2\].
Thử lại:
Với \[m = – 1\] thì \[y = \frac{{{x^2} + 2x – 2}}{{x – 1}} = x + 3 + \frac{1}{{x – 1}} \Rightarrow y’ = 1 – \frac{1}{{{{\left( {x – 1} \right)}^2}}}\]
Do đó \[y” = \frac{2}{{{{\left( {x – 1} \right)}^3}}} \Rightarrow y”\left( 0 \right) = – 2 < 0 \Rightarrow x = 0\] là điểm cực đại của hàm số: loại.
Với \[m = 2\] thì \[y = \frac{{{x^2} – x – 2}}{{x + 2}} = x – 3 + \frac{4}{{x + 2}} \Rightarrow y’ = 1 – \frac{4}{{{{\left( {x + 2} \right)}^2}}}\]
Do đó \[y” = \frac{8}{{{{\left( {x + 2} \right)}^3}}} \Rightarrow y”\left( 0 \right) = 1 > 0\] nên \[x = 0\] là điểm cực tiểu của hàm số. Vậy giá trị cần tìm \[m = 2\].
Bài toán 3. Tìm hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\] sao cho hàm số f đạt cực tiểu tại điểm \[x = 0,f\left( 0 \right) = 0\] và đạt cực đại tại điểm \[x = 1,f\left( 1 \right) = 1\].
Giải
Ta có \[f’\left( x \right) = 3a{x^2} + 2bx + c\]. Vì \[f\left( 0 \right) = 0\] nên \[d = 0\]. Hàm số đạt cực tiểu tại điểm \[x = 0\] nên \[f’\left( 0 \right) = 0\] do đó \[c = 0\].
Vì \[f\left( 1 \right) = 1\] nên \[a + b = 1\]. Hàm số đạt cực đại tại điểm \[x = 1\] nên \[f’\left( 1 \right) = 0\] do đó \[3a + 2b = 0\].
Ta có hệ phương trình \[\left\{ \begin{array}{l}a + b = 1\\3a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 2\\b = 3\end{array} \right.\]
Thử lại:
\[f\left( x \right) = – 2{x^3} + 3{x^2},f’\left( x \right) = – 6{x^2} + 6x,f”\left( x \right) = – 12x + 6\]
\[f”\left( 0 \right) = 6 > 0\]. Hàm số đạt cực tiểu tại điểm \[x = 0\]: thỏa mãn.
\[f”\left( 1 \right) = – 6 < 0\]. Hàm số đạt cực đại tại điểm \[x = 1\]: thỏa mãn.
Bài toán 4. Tìm các số thực p và q sao cho hàm số \[f\left( x \right) = x + p + \frac{q}{{x + 1}}\] đạt cực đại tại điểm \[\left( { – 2; – 2} \right)\].
Giải
Ta có \[f’\left( x \right) = 1 – \frac{q}{{{{\left( {x + 1} \right)}^2}}},\] với mọi \[x \ne – 1\].
Nếu \[q \le 0\] thì \[f’\left( x \right) > 0\] với mọi \[x \ne – 1\]. Hàm số không có cực đại, cực tiểu: loại.
Nếu \[q > 0\] thì phương trình: \[f’\left( x \right) = \frac{{{x^2} + 2x + 1 – q}}{{{{\left( {x + 1} \right)}^2}}} = 0\] có hai nghiệm phân biệt \[{x_1} = – 1 – \sqrt q \] và \[{x_2} = – 1 + \sqrt q \].
BBT:
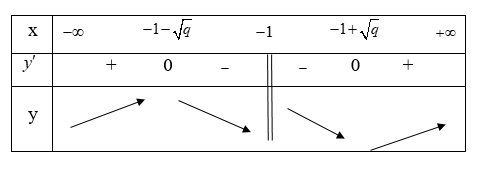
Hàm số đạt cực đại tại điểm \[\left( {2; – 2} \right)\] khi và chỉ khi
\[\left\{ \begin{array}{l} – 1 – \sqrt q = – 2\\f\left( { – 2} \right) = – 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt q = 1\\p = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}q = 1\\p = 1\end{array} \right.\].
Bài toán 5. Tìm a để đồ thị hàm số \[y = \frac{1}{3}{x^2} + \frac{1}{2}a{x^2} + x + 7\] có 2 cực trị và hoành độ 2 điểm cực trị của hàm số đó thỏa mãn \[\frac{{x_1^2}}{{x_2^2}} + \frac{{x_2^2}}{{x_1^2}} > 7\].
Giải
\[D = \mathbb{R}\]. Ta có \[y’ = {x^2} + ax + 1\]
Vì \[y’\] là hàm số bậc hai nên hàm số có 2 cực trị khi và chỉ khi \[y’\left( x \right) = 0\] có hai nghiệm phân biệt \[ \Leftrightarrow \Delta > 0 \Leftrightarrow {a^2} – 4 > 0 \Leftrightarrow a < – 2\] hoặc \[a > 2\].
Gọi \[{x_1}\] và \[{x_2}\] là hai nghiệm của \[y’\left( x \right) = 0\] thì \[S = {x_1} + {x_2} = – a,P = {x_1}{x_2} = 1\].
Ta có: \[\frac{{x_1^2}}{{x_2^2}} + \frac{{x_2^2}}{{x_1^2}} > 7 \Leftrightarrow {\left( {\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}}} \right)^2} – 2 > 7 \Leftrightarrow {\left( {\frac{{x_1^2 + x_2^2}}{{{x_1}{x_2}}}} \right)^2} > 9\]
\[ \Leftrightarrow \left( {\frac{{{S^2} – 2{P^2}}}{P}} \right) > 9 \Leftrightarrow {\left( {{a^2} – 2} \right)^2} > 9 \Leftrightarrow {a^2} > 5\]
Chọn giá trị \[a < – \sqrt 5 \] hoặc \[a > \sqrt 5 \].
Bài toán 6. Tìm m để hàm số: \[y = \frac{{{x^2} + 2mx + 1 – 3{m^2}}}{{x – m}}\] có hai điểm cực trị nằm về hai phía của trục Oy.
Giải
Điều kiện \[x \ne m\]. Ta có \[y’ = \frac{{{x^2} – 2mx + {m^2} – 1}}{{{{\left( {x – m} \right)}^2}}}\]
Đồ thị có 2 cực trị ở 2 phía của trục tung
\[ \Leftrightarrow y’ = 0\] có 2 nghiệm \[{x_1},{x_2} \ne m\] và \[{x_1}{x_2} < 0\]
\[ \Leftrightarrow {m^2} – 1 < 0 \Leftrightarrow – 1 < m < 1\].
Bài toán 7. Tìm m để hàm số: \[y = \frac{{m{x^2} + \left( {2 – 4m} \right)x + 4m + 1}}{{x – 1}}\] có 2 cực trị và hai giá trị cực trị trái dấu.
Giải
Điều kiện: \[x \ne 1\].
Ta có \[y’ = \frac{{m{x^2} – 2mx – 3}}{{{{\left( {x – 1} \right)}^2}}}\], đặt \[g\left( x \right) = m{x^2} – 2mx – 3\].
Đồ thị có 2 cực trị \[ \Leftrightarrow m \ne 0,\Delta ‘ > 0,g\left( x \right) \ne 0 \Leftrightarrow m < – 3\] hoặc \[m > 0\].
Ta có \[{x_1} + {x_2} = 2,{x_1}{x_2} = – \frac{3}{m}\] nên
\[ \Leftrightarrow \left( {2m{x_1} + 2 – 4m} \right)\left( {2m{x_2} + 2 – 4m} \right) < 0\]
\[ \Leftrightarrow 4{m^2}{x_1}{x_2} + 2m\left( {2 – 4m} \right)\left( {{x_1} + {x_2}} \right) + {\left( {2 – 4m} \right)^2} < 0\]
\[ \Leftrightarrow – 12m + 2m\left( {2 – 4m} \right) + {\left( {2 – 4m} \right)^2} < 0 \Leftrightarrow 4 – 20m < 0 \Leftrightarrow m > \frac{1}{5}\].
Bài toán 8. Tìm m để đồ thị \[y = \frac{{{x^2} + 2\left( {m + 1} \right)x + {m^2} + 4m}}{{x + 2}}\] có cực đại và cực tiểu, đồng thời các điểm cực trị cùng với gốc tọa độ tạo thành tam giác vuông tại O.
Giải
Điều kiện \[x \ne – 2\], \[y’ = \frac{{{x^2} + 4x + 4 – {m^2}}}{{{{\left( {x + 2} \right)}^2}}}\]
\[y’ = 0 \Leftrightarrow {\left( {x + 2} \right)^2} = {m^2} \Leftrightarrow x = – 2 \pm m\]
Hàm số có 2 cực trị khi \[m \ne 0\] là: \[A\left( { – 2 – m; – 2} \right),B\left( { – 2 + m;4m – 2} \right)\]
Tam giác OAB vuông tại O \[ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0\]
\[ \Leftrightarrow \left( { – m – 2} \right)\left( {m – 2} \right) + \left( { – 2} \right)\left( {4m – 2} \right) = 0 \Leftrightarrow – {m^2} – 8m + 8 = 0\]
\[ \Leftrightarrow m = – 4 \pm 2\sqrt 6 \] (thỏa mãn)
Bài toán 9. Tìm m để đồ thị hàm số: \[y = {x^3} – 3{x^2} + mx + 1\] có cực đại, cực tiểu và hai điểm đó cách đều đường thẳng \[d:y = – 2x\].
Giải
\[D = \mathbb{R}\]. Ta có \[y’ = 3{x^2} – 6x + m\].
Điều kiện có CĐ và CT là \[\Delta ‘ = 9 – 3m > 0 \Leftrightarrow m < 3\].
Ta có \[y = \left( {\frac{1}{3}x – \frac{1}{3}} \right)y’ + 2\left( {\frac{1}{3}m – 1} \right)x + \frac{1}{3}m + 1\] nên đường thẳng qua 2 điểm CĐ, CT là \[d’:y = 2\left( {\frac{1}{3}m – 1} \right)x + \frac{1}{3}m + 1\].
Điều kiện CĐ, CT cách đều \[d:y = – 2x\] là \[d’\] hoặc song song với d hoặc d đi qua trung điểm \[I\left( {1;m – 1} \right)\] của đoạn nối CĐ, CT.
\[2\left( {\frac{1}{3}m – 1} \right) = – 2,\frac{1}{3}m + 1 \ne 0\] hoặc \[m – 1 = – 2.1 \Leftrightarrow m = 0\] hoặc \[m = – 1\] (chọn).
Bài toán 10. Viết phương trình đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị:
\[y = {x^3} + 3m{x^2} + 3\left( {{m^2} – 1} \right)x + {m^3} – 3m\].
Giải
Tập xác định \[D = \mathbb{R}\].
\[y’ = 3{x^2} + 6mx + 3\left( {{m^2} – 1} \right),\Delta ‘ = 1 > 0,\forall x\] nên đồ thị luôn luôn có CĐ và CT với hoành độ \[{x_1},{x_2}\].
Lấy \[y\left( x \right)\] chia cho \[y’\left( x \right)\] ta có: \[y\left( x \right) = \left( {\frac{1}{3}x + \frac{m}{3}} \right)y’\left( x \right) – 2\left( {x + m} \right)\].
Do đó: \[{y_1} = y\left( {{x_1}} \right) = \left( {\frac{1}{3}{x_1} + \frac{m}{3}} \right)y’\left( {{x_1}} \right) – 2\left( {{x_1} + m} \right) = – 2\left( {{x_1} + m} \right)\]
và \[{y_2} = y\left( {{x_2}} \right) = \left( {\frac{1}{3}{x_2} + \frac{m}{3}} \right)y’\left( {{x_2}} \right) – 2\left( {{x_2} + m} \right) = – 2\left( {{x_2} + m} \right)\]
nên đường thẳng qua CĐ, CT là \[y = – 2\left( {x + m} \right)\].
Xem thêm