Câu hỏi:
Từ vị trí A, người ta quan sát một cây thông. Biết AH = 5 m, HB = 15 m, \(\widehat {BAC} = 45^\circ \).

Chiều cao của cây bằng:
A. 12,5 m;
Đáp án chính xác
B. 13,5 m;
C. 14,5 m;
D. 15,5 m.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A.
Trong tam giác ABH vuông tại H ta có:
\({\rm{AB}}\,{\rm{ = }}\,\sqrt {A{H^2} + H{B^2}} = \sqrt {{5^2} + {{15}^2}} = 5\sqrt {10} \).
Lại có: tan \(\widehat {ABH}\)= \(\frac{{AH}}{{HB}}\)= \(\frac{1}{3}\)\( \Rightarrow \)\(\widehat {ABH}\)≈18,43°.
\(\widehat {ABC} = 90^\circ – \widehat {ABH} \approx 71,57^\circ \) \( \Rightarrow \widehat {ACB} = 180^\circ – \widehat {CAB} – \widehat {ABC} \approx 63,43^\circ \).
Theo định lý sin trong tam giác ABC ta có:
\(\frac{{CB}}{{\sin \widehat {CAB}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\) \( \Rightarrow \)CB ≈ \(\frac{{5\sqrt {10} .\sin 45^\circ }}{{\sin 63,43^\circ }}\)≈12,5.
Chiều cao của cây khoảng 12,5 m.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
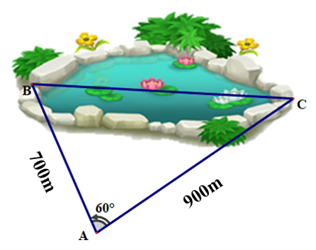
- Tính khoảng cách giữa hai điểm ở hai đầu của một ao cá nhà bác An. Biết khoảng cách từ chỗ bác An đứng đến hai đầu ao lần lượt là 700 m và 900 m và bác An quan sát nhìn hai điểm này dưới một góc 60° như hình vẽ.
Câu hỏi:
Tính khoảng cách giữa hai điểm ở hai đầu của một ao cá nhà bác An. Biết khoảng cách từ chỗ bác An đứng đến hai đầu ao lần lượt là 700 m và 900 m và bác An quan sát nhìn hai điểm này dưới một góc 60° như hình vẽ.
Trả lời:
Hướng dẫn giải:
Theo định lí côsin ta có:
\(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.cosA\)
\( = {700^2} + {900^2} – 2.700.900.cos60^\circ \)= 670 000.
Suy ra: BC = \(\sqrt {670000} \approx 818,5\)(m).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ).
Biết BC = 5 m, \(\widehat {ACB} = 45^\circ ,\widehat {CBA} = 50^\circ \). Chiều cao của cây bằng bao nhiêu?
Câu hỏi:
Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ).
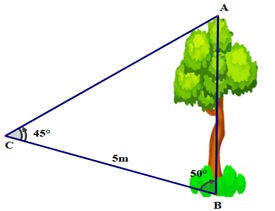
Biết BC = 5 m, \(\widehat {ACB} = 45^\circ ,\widehat {CBA} = 50^\circ \). Chiều cao của cây bằng bao nhiêu?Trả lời:
Hướng dẫn giải:
Áp dụng định lí tổng 3 góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)\( \Rightarrow \widehat A = 85^\circ \).
Theo định lí sin ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)\( \Leftrightarrow \frac{{AB}}{{\sin 45^\circ }} = \frac{5}{{\sin 85^\circ }}\)\( \Leftrightarrow AB = \sin 45^\circ .\frac{5}{{\sin 85^\circ }}\)≈ 3,55 (m).
Vậy chiều cao của cây khoảng 3,55 m.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Khoảng cách từ A đến B không thể đo trực tiếp vì phải qua một đầm lầy nên người ta làm như sau: Xác định một điểm C sao cho ta đo được AC = 15 m, BC = 21 m và \(\widehat {ACB} = 80^\circ \). Khoảng cách AB gần nhất với kết quả nào dưới đây?
Câu hỏi:
Khoảng cách từ A đến B không thể đo trực tiếp vì phải qua một đầm lầy nên người ta làm như sau: Xác định một điểm C sao cho ta đo được AC = 15 m, BC = 21 m và \(\widehat {ACB} = 80^\circ \). Khoảng cách AB gần nhất với kết quả nào dưới đây?
A. 20 m;
B. 24 m;
Đáp án chính xác
C. 30 m;
D. 34 m.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B.
Ta mô phỏng bài toán như hình vẽ sau:
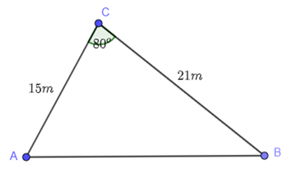
Theo định lí côsin ta có:
\(A{B^2} = B{C^2} + A{C^2} – 2.BC.AC.\cos C\).
Thay số: \(A{B^2} = {21^2} + {15^2} – 2.21.15.\cos 80^\circ \)≈ 556,6
Suy ra: AB ≈ \(\sqrt {556,6} \)≈ 23,6 (m).
Vậy khoảng cách AB là khoảng 23,6 m và gần nhất với kết quả 24 m.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc \(\widehat {COD} = 60^\circ \).
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?
Câu hỏi:
Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc \(\widehat {COD} = 60^\circ \).
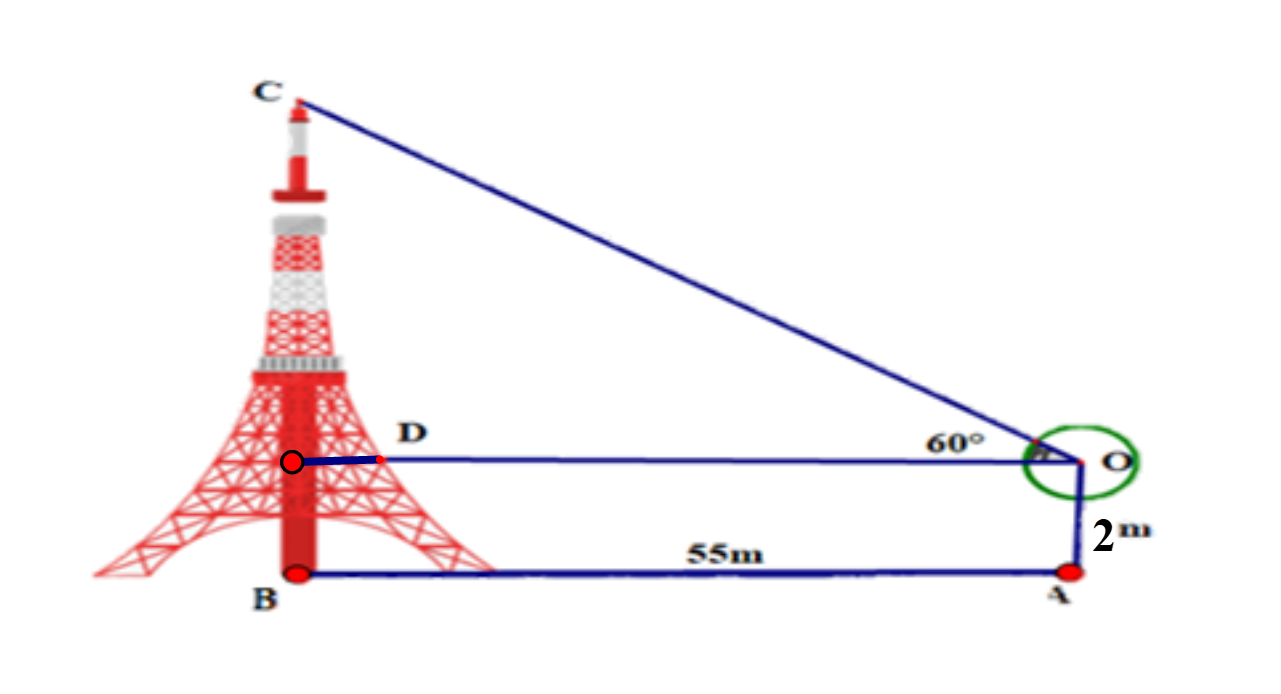
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?A. 87 m;
B. 90 m;
C. 97 m;
Đáp án chính xác
D. 100 m.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: C.
Xét tam giác OCD vuông tại D có OD = AB = 55 (m); \(\widehat {COD} = 60^\circ \)
Nên CD = OD. tan\(\widehat {COD}\) = 55\(\sqrt 3 \)≈ 95,26 (m).
Vậy chiều cao của tháp là: 95,26 + 2 = 97,26 (m).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang góc 15°30′.
Hỏi điểm pháo hoa nổ cao so với mặt đất gần với giá trị nào sau đây?
Câu hỏi:
Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang góc 15°30′.
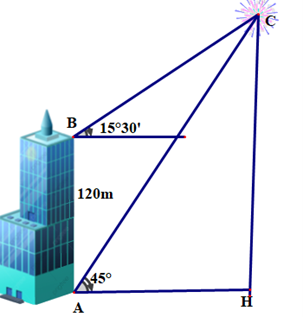
Hỏi điểm pháo hoa nổ cao so với mặt đất gần với giá trị nào sau đây?A. 166 m;
Đáp án chính xác
B. 266 m;
C. 250 m;
D. 300 m.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có: \(\widehat {BAC} = \widehat {BAH} – \widehat {CAH} = 90^\circ – 45^\circ = 45^\circ \).
Lại có: \(\widehat {ABC} = 90^\circ + 15^\circ 30′ = 105^\circ 30’\).
Trong tam giác ABC có: \(\widehat {BCA} = 180^\circ – \left( {\widehat {BAC} + \widehat {ABC}} \right) = 29^\circ 30’\).
Áp dụng định lí sin vào ∆ABC ta có:
\(\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{AB}}{{\sin \widehat {BCA}}}\)\( \Rightarrow \)AC = \(\sin \widehat {ABC}.\frac{{AB}}{{\sin \widehat {BCA}}}\)≈ 234,83 (m).
Trong tam giác vuông AHC có: \(\frac{{CH}}{{AC}} = \sin 45^\circ \)\( \Rightarrow \)CH = AC. sin 45° ≈ 166,05.
Vậy điểm pháo hoa nổ cao so với mặt đất khoảng 166,05 m.====== **** mời các bạn xem câu tiếp bên dưới **** =====