SBT Toán 9 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn | Giải SBT Toán lớp 9

Giải SBT Toán 9 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn

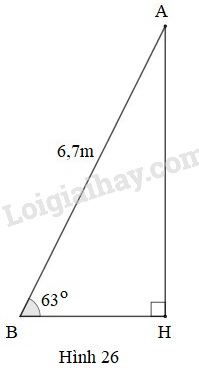
Bài 72 trang 117 SBT Toán 9 tập 1: Thang AB dài $6,7m$ tựa vào tường làm thành góc ${63}^{\circ }$ với mặt đất (h.26). Hỏi chiều cao của thang đạt được so với mặt đất ?

Phương pháp giải:

– Chiều cao của thang là cạnh góc vuông đối diện với góc .

– Tìm độ dài cạnh góc vuông ta lấy độ dài cạnh huyền nhân với sin góc đối diện.

Lời giải:

Xét tam giác $AHB$  vuông tại $H,$ ta có:

$AH=AB.\sin \hat{B}=6,7.\sin {63}^{\circ }$ $\approx 6(m)$

Vậy chiều cao của cái thang đạt được so với mặt đất là $6m$.

Bài 73 trang 117 SBT Toán 9 tập 1: Làm dây kéo cờ: Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ
(chiếu bởi ánh sáng mặt trời) dài \(11,6m\) và góc nhìn mặt trời là \(36^\circ 50’\) (h.27)

Phương pháp giải:

– Chiều cao của cột cờ là cạnh góc vuông đối diện với góc \(36^\circ 50’\), bóng cột cờ là cạnh kề với góc nhọn.

– Tìm độ dài cạnh góc vuông ta lấy độ dài cạnh góc vuông kia nhân với tang góc đối.

– Chiều dài của dây kéo cờ gấp 2 lần chiều cao của cột cờ.

Lời giải:

Theo hệ thức giữa cạnh và đường cao trong tam giác vuông ta suy ra chiều cao cột cờ là :  $11,6.\tan {36}^{\circ }{50}^{\prime }\approx 8,69(m)$

Chiều dài của dây kéo cờ là : $8,69.2=17,38(m)$

Bài 74 trang 117 SBT Toán 9 tập 1: Bài toán con mèo

Một con mèo ở trên cành cây cao $6,5m$. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó, khi đó góc của thang với mặt đất là bao nhiêu, biết chiếc thang dài $6,7m$ ?

Phương pháp giải:

– Độ cao của con mèo chính là cạnh góc vuông đối diện với góc tạo bởi cái thang và mặt đất, chiều dài thang là cạnh huyền.

– Gọi $\alpha$ là góc tạo bởi cái thang và mặt đất, ta tìm $\sin \alpha$ bằng cách lấy $6,5$ chia cho $6,7$ (cạnh đối chia cạnh huyền), từ đó tìm được góc $\alpha$. 

Lời giải:

 

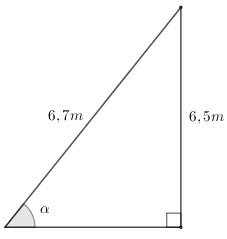
Gọi $\alpha$ là góc tạo bởi cái thang và mặt đất.

Ta có: $\sin \alpha =\frac{6,5}{6,7}\approx 0,9701$

Suy ra: $\alpha \approx {75}^{\circ }{57}^{\prime }$

Vậy góc của thang so với mặt đất là ${75}^{\circ }{57}^{\prime }$.

Bài 75 trang 118 SBT Toán 9 tập 1: Bài toán đài quan sát

Đài quan sát ở Toronto, Ontario, Canada cao $533m$. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo thành bóng dài $1100m$. Hỏi lúc đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu ? 

Phương pháp giải:

– Chiều cao của đài quan sát là cạnh góc vuông đối diện với góc nhọn, bóng của nó trên mặt đất là cạnh góc vuông kề với góc nhọn.

– Gọi $\alpha$ là góc tạo bởi  tia sáng mặt trời và mặt đất, ta tìm $tg\alpha$ bằng cách lấy $533$ chia cho $1100$, từ đó tìm được góc $\alpha$. 

Lời giải:

 

Gọi $\alpha$ là góc tạo bởi  tia sáng mặt trời và mặt đất.

Ta có: $tg\alpha =\frac{533}{1100}\approx 0,4845$.

Suy ra: $\alpha \approx {25}^{\circ }{51}^{\prime }$.

Vậy góc tạo bởi tia sáng mặt trời và mặt đất là ${25}^{\circ }{51}^{\prime }$

Bài 76 trang 118 SBT Toán 9 tập 1: Bài toán hải đăng

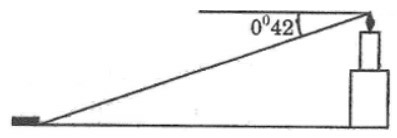
Một người quan sát ở đài hải đăng cao 80 feet (đơn vị đo lường Anh) so với mặt nước biển, nhìn một chiếc tàu ở xa với góc $0^{\circ }{42}^{\prime }$. Hỏi khoảng cách từ tàu đến chân hải đăng tính theo đơn vị hải lí là bao nhiêu? (1 hải lí = 5280 feet) (h.28). 

Phương pháp giải:

– Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc $0^{\circ }{42}^{\prime }$, khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn. 

– Tìm độ dài cạnh góc vuông ta có thể lấy độ dài cạnh góc vuông kia nhân với côtang góc kề.

Lời giải:

Ta có : Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc $0^{\circ }{42}^{\prime }$, khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn. 

Vậy khoảng cách từ tàu đến chân ngọn hải đăng là :

$80.\cot 0^{\circ }{42}^{\prime }\approx 6547,76$ (feet) $\approx 1,24$ (hải lí)

Bài 77 trang 118 SBT Toán 9 tập 1: Bài toán máy bay hạ cánh  

Một máy bay đang bay ở độ cao $10km$. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu phi công muốn tạo góc nghiêng $3^{\circ }$ thì cách sân bay bao nhiêu ki-lô-mét phải bắt đầu cho máy bay hạ cánh ?

b) Nếu cách sân bay $300km$ máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu? 

Phương pháp giải:

– Độ cao của máy bay là cạnh góc vuông đối diện với góc nghiêng so với mặt đất. Khoảng cách từ máy bay đến sân bay là cạnh huyền. 

– Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền nhân với sin góc đổi, từ đó tìm cạnh huyền ta lấy cạnh góc vuông chia cho sin góc đổi.

– Gọi $\beta$ là góc nghiêng của đường đi máy bay so với mặt đất. Tìm tìm $\sin \beta$ bằng cách tìm tỉ số của $10km$ và $300km$, từ đó tìm được góc $\beta$. 

Lời giải:

a) Ta có hình vẽ: Độ cao máy bay là $AB=10km$, góc nghiêng $\hat{C}=3^0$. Ta tính BC. 

 

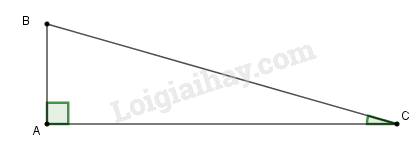
Vậy khoảng cách từ máy bay đến sân bay là:

$BC=\frac{AB}{\sin \hat{C}}$$=\frac{10}{\sin 3^{\circ }}\approx 191(km)$

b) Ta có hình vẽ: Khi đó $AB=10km,BC=300km$ 

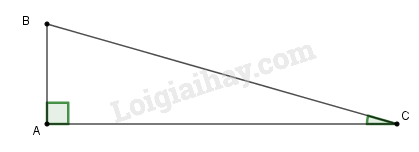
Gọi $\hat{C}=\beta$ là góc nghiêng của đường đi máy bay so với mặt đất. 

Ta có : $\sin \beta =\frac{AB}{BC}$$=\frac{10}{300}=\frac{1}{30}$.

Suy ra: $\beta \approx 1^{\circ }{55}^{\prime }$.

Nếu cách sân bay $300km$ máy bay bắt đầu hạ cánh thì góc nghiêng là $1^{\circ }{55}^{\prime }$.

Bài 78 trang 118 SBT Toán 9 tập 1: Bài toán chiếu xạ chữa bệnh

Một khối u của một căn bệnh nhân cách mặt da $5,7cm$, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) $8,3cm$ (h.29).

a) Hỏi góc tạo bởi chùm tia với mặt da?

b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?

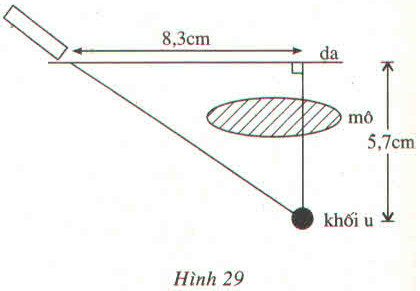
Phương pháp giải:

– Khoảng cách từ mặt da đến khối u là cạnh góc vuông đối diện với góc nhọn, khoảng cách từ chùm tia đến mặt da là cạnh kề.

– Gọi $\beta$ là góc tạo bởi chùm tia với mặt da. Tìm tìm $tg\beta$ bằng cách tìm tỉ số của $5,7cm$ và $8,3cm$, từ đó tìm được góc $\beta$.

– Tìm độ dài từ chùm tia đến khối u ta lấy khoảng cách từ mặt da đến khối u chia cho $\sin \beta$.

Lời giải:

a) Khoảng cách từ mặt da đến khối u là cạnh góc vuông đối diện với góc nhọn, khoảng cách từ chùm tia đến mặt da là cạnh kề.

Gọi $\beta$ là góc tạo bởi chùm tia với mặt da.

Ta có: $tg\beta =\frac{5,7}{8,3}\approx 0,6867$.

Suy ra: $\beta \approx {34}^{\circ }{29}^{\prime }.$

Vậy góc tạo bởi chùm tia với mặt da là ${34}^{\circ }{29}^{\prime }$. 

b) Đoạn đường chùm tia đi đến khối u là:  

$\frac{5,7}{\sin {34}^{\circ }{29}^{\prime }}\approx 10,07(cm)$.

Bài 79 trang 119 SBT Toán 9 tập 1: Bài toán tàu ngầm

Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc ${21}^{\circ }$ (h.30)

a) Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu?

b) Tàu phải chạy bao nhiêu mét để đạt đến độ sâu 1000m?

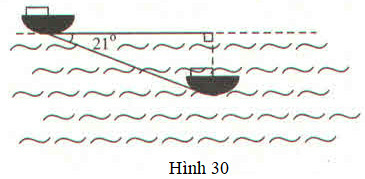
Phương pháp giải:

– Độ sâu của tàu là cạnh góc vuông đối diện với góc ${21}^{\circ }$, đoạn đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.

– Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc côsin góc kề.

Lời giải:

a) Độ sâu của tàu là cạnh góc vuông đối diện với góc ${21}^{\circ }$, đoạn đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.

Độ sâu của tàu đạt được là:     

$300.\sin {21}^{\circ }\approx 107,5(m)$

Khoảng cách từ tàu đến nơi xuất phát theo phương nằm ngang là:

$300.\cos {21}^{\circ }\approx 280(m)$

b) Đoạn đường tàu đi được là: 

$\frac{1000}{\sin {21}^{\circ }}\approx 2790(m)$

Bài tập bổ sung (trang 119 SBT Toán 9)

Bài 5.1 trang 119 SBT Toán 9 tập 1: (h.bs. 5). Mô tả cánh của một máy bay. Hãy tính các độ dài $AC,BD,AB$ của cánh máy bay theo số liệu được cho trong hình đó.

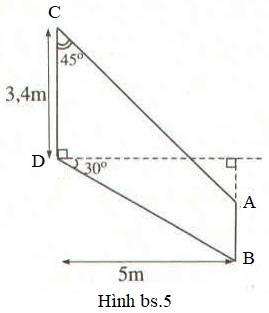
Phương pháp giải:

Áp dụng các hệ thức lượng trong tam giác vuông để tìm độ dài các cạnh $AC,BD,AB$.

Lời giải:

Đường thẳng $AC$ cắt đường thẳng vuông góc với $CD$ tại $D$ ở điểm $H$ thì tam giác $CDH$ là tam giác vuông cân (vì là tam giác vuông có góc C bằng ${45}^0$), $DH=CD=3,4m$.

Đường thẳng $AB$ cắt $DH$ tại $K$ thì $DK=5m$ nên $H$ nằm ở giữa $D$ và $K$ (xem Hình bs.6).

Dựng hình chữ nhật $AKDI$ thì $AIC$ là tam giác vuông cân (vì là tam giác vuông có góc C bằng ${45}^0$), $AI=KD=5m$

Xét tam giác vuông AIC ta có: $AC=\sqrt{A{I}^2+I{C}^2}=\sqrt{5^2+5^2}=5\sqrt{2}(m)$

Trong tam giác vuông $BKD$, có:

$DB=\frac{DK}{\cos {30}^{\circ }}=\frac{5}{\frac{\sqrt{3}}{2}}=\frac{10}{\sqrt{3}}$ $=\frac{10\sqrt{3}}{3}\approx 5,77(m)$

Vì $DC//AK$ (cùng vuông với DK) nên $\widehat{KAH}=\hat{C}={45}^0$ (hai góc ở vị trí so le trong)

Suy ra $HKA$ là tam giác vuông cân (tam giác vuông có góc A bằng ${45}^0$)

Do đó: $AK=HK=DK–DH=DK–DC$ $=5–3,4=1,6m$. 

Xét tam giác vuông BDK, ta có: $KB=DK.tg{30}^{\circ }$ $=5.\frac{\sqrt{3}}{3}$ $=\frac{5\sqrt{3}}{3}$.  

Suy ra : $AB=KB–KA$ $=\frac{5\sqrt{3}}{3}-1,6\approx 1,29(m)$.