Cho chuyển động thẳng xác định bởi phương trình S = t3 – 3t2 – 9t, trong đó t được tính bằng giây (s) và S được tính bằng mét (m).a.Tính vận tốc của chuyển động khi t = 2s.b.Tính gia tốc của chuyển động khi t = 3s.c.Tính gia tốc tại thời điểm vận tốc triệt tiêu.d.Tính vận tốc tại thời điểm gia tốc triệt tiêu.

Câu hỏi:

Cho chuyển động thẳng xác định bởi phương trình $S = t^3 – 3t^2 – 9t$, trong đó t được tính bằng giây (s) và S được tính bằng mét (m).a.Tính vận tốc của chuyển động khi $t = 2s$.b.Tính gia tốc của chuyển động khi $t = 3s$.c.Tính gia tốc tại thời điểm vận tốc triệt tiêu.d.Tính vận tốc tại thời điểm gia tốc triệt tiêu.

Trả lời:

Vận tốc: v(t) = S’(t) = (t3 – 3t2 – 9t)’ = 3t2 – 6t – 9.Gia tốc : a(t) = v’(t) = (3t2 – 6t – 9)’ = 6t – 6.a) Khi t = 2s, v(2) = 3.22 – 6.2 – 9 = -9 (m/s).b) Khi t = 3s, a(3) = 6.3 – 6 = 12 (m/s2).c) v(t) = 0 ⇔ 3t2 – 6t – 9 = 0 ⇔ t = 3 (vì t > 0).Khi đó a(3) = 12 m/s2.d) a(t) = 0 ⇔ 6t – 6 = 0 ⇔ t = 1.Khi đó v(1) = 3.12 – 6.1 – 9 = -12 (m/s).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Chương 5 (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 7
   Lý thuyết Toán lớp 7 Chương 5

   Tổng hợp lý thuyết Toán 7 Chương 5

   1. Thu thập dữ liệu

   Ta có thể thu thập dữ liệu từ những nguồn văn bản, bảng biểu, hình ảnh trong thực tiễn.

   Ví dụ: Hình ảnh trên bản tin thời tiết tại TP Hồ Chí Minh:

   

   Từ hình ảnh trên ta có bảng thống kê sau:

   

   2. Phân loại dữ liệu theo các tiêu chí

   – Các dữ liệu là số được gọi là dữ liệu định lượng.

   – Các dữ liệu không phải số gọi là dữ liệu định tính.

   – Để thuận tiện trong mô tả và xử lý, người ta thường phải phân loại dữ liệu:

   + Dữ liệu định lượng được biểu diễn bằng số thực.

   + Dữ liệu định tính được biểu diễn bằng từ, chữ, kí hiệu,…

   3. Tính hợp lý của dữ liệu

   Để đảm bảo tính hợp lý, dữ liệu cần phải đáp ứng các tiêu chí toán học đơn giản, chẳng hạn như:

   – Tổng tỉ lệ phần trăm của tất cả các thành phần phải bằng 100%.

   – Số lượng của bộ phận phải nhỏ hơn số lượng của toàn thể; …

   – Phải có tính đại diện đối với vấn đề cần thống kê.

   4. Ôn tập về biểu đồ hình quạt tròn

   – Để biểu thị tỉ lệ phần trăm của từng loại số liệu so với toàn thể, ta thường sử dụng biểu đồ hình quạt tròn. Đó là biểu đồ có dạng hình tròn được chia thành các hình quạt. Tỉ số diện tích của tường hình quạt so với cả hình tròn biểu thị tỉ lệ phần trăm của từng số liệu tương ứng.

   – Để đọc một biểu đồ hình quạt tròn, ta cần thực hiện như sau:

   + Xác định số đối tượng được biểu thị bằng cách đếm số hình quạt có trong hình tròn.

   + Đọc ghi chú của biểu đồ để biết tên các đối tượng.

   + Xác định tỉ lệ phần trăm của từng đối tượng so với toàn thể bằng cách đọc số ghi trên biểu đồ.

   5. Biểu diễn dữ liệu vào biểu đồ hình quạt tròn

   Để biểu diễn thông tin từ bảng thống kê vào biểu đồ hình quạt tròn, ta thực hiện các bước sau:

   Bước 1: Xử lý số liệu

   – Tính tổng các số liệu.

   – Tính tỉ lệ phần trăm của từng số liệu so với toàn thể.

   Bước 2: Biểu diễn số liệu

   – Ghi tên biểu đồ.

   – Ghi chú tên các đối tượng.

   – Ghi chú các tỉ lệ phần trăm trên biểu đồ.

   6. Phân tích dữ liệu trên biểu đồ hình quạt tròn

   Muốn phân tích dữ liệu được biểu diễn trên biểu đồ hình quạt tròn, ta nên chú ý các đặc điểm sau :

   – Biểu đồ biểu diễn các thông tin về vấn đề gì ?

   – Có bao nhiêu đối tượng được biểu diễn ?

   – Đối tượng nào chiếm tỉ lệ phần trăm cao nhất ?

   – Đối tượng nào chiếm tỉ lệ phần trăm thấp nhất ?

   – Tương quan về tỉ lệ phần trăm giữa các đối tượng.

   7. Giới thiệu biểu đồ đoạn thẳng

   Để biểu diễn sự thay đổi số liệu của một số đối tượng theo thời gian, người ta thường dùng biểu đồ đoạn thẳng.

   Biểu đồ đoạn thẳng gồm :

   – Hai trục vuông góc : trục ngang biểu diễn các mốc thời gian, trục thẳng đứng biểu diễn độ lớn của dữ liệu.

   – Các đoạn thẳng nối nhau tạo thành một đường gấp khúc cho ta thấy sự thay đổi của dữ liệu theo các mốc thời gian.

   8. Vẽ biểu đồ đoạn thẳng

   Ví dụ : Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu trong bảng thống kê dưới đây :

   

   Bước 1: Vẽ hai thanh ngang và thẳng đứng vuông góc với nhau.

   – Trục ngang: Ghi các mốc thời gian

   – Trục thẳng đứng: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia.

   Bước 2:

   – Tại mỗi mốc chia thời gian trên trục ngang, đánh dấu một điểm cách mốc thời gian theo chiều thẳng đứng một khoảng bằng số liệu tại mốc thời gian đó, tương ứng với khoảng chia trên trục.

   – Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi của số liệu theo thời gian.

   

   Bước 3: Hoàn thiện biểu đồ

   – Ghi tên biểu đồ.

   – Ghi chú các giá trị số liệu tại các đầu đoạn thẳng.

   – Ghi đơn vị trên hai trục.

   

   9. Đọc và phân tích dữ liệu từ biểu đồ đoạn thẳng

   Muốn đọc và phân tích dữ liệu được biểu diễn trên biểu đồ đoạn thẳng, ta cần chú ý các đặc điểm sau:

   – Biểu đồ biểu diễn các thông tin về vấn đề gì?

   – Đơn vị thời gian là gì ?

   – Thời điểm nào số liệu cao nhất ?

   – Thời điểm nào số liệu thấp nhất ?

   – Số liệu tăng trong những khoảng thời gian nào?

   – Số liệu giảm trong những khoảng thời gian nào?

   Bài tập Tổng hợp Toán 7 Chương 5

   Bài 1: Phân loại các dãy dữ liệu sau dựa trên các tiêu chí định tính và định lượng.

   a) Thời gian chạy 100 m (tính theo giây) của các học sinh lớp 7 là : 16 ; 17 ; 18 ; 19.

   b) Danh sách các môn học yêu thích của một bạn học sinh là: toán , vật lý, tiếng anh, âm nhạc, mĩ thuật.

   c) Các giải thưởng thi học sinh giỏi môn Toán cấp tỉnh là : giải nhất, giải nhì, giải ba, giải khuyến khích.

   Hướng dẫn giải

   a) Dữ liệu thời gian chạy được biểu diễn bằng số thực (tính theo giây: 16; 17; 18; 19) nên nó là dữ liệu định lượng.

   b) Dữ liệu môn học yêu thích được biểu diễn bằng từ (toán , vật lý, tiếng anh, âm nhạc, mĩ thuật ) nên nó là dữ liệu định tính.

   c) Dữ liệu các giải thưởng được biểu diễn bằng từ (giải nhất, giải nhì, giải ba, giải khuyến khích) nên nó là dữ liệu định tính.

   Bài 2: Kết quả tìm hiểu về khả năng đá bóng của các bạn học sinh lớp 7C được cho bởi bảng thống kê sau :

   

   a) Hãy phân loại các dữ liệu cho trong bảng trên dựa trên tiêu chí định tính và định lượng.

   b) Dữ liệu trên có đại diện được cho khả năng đá bóng của các bạn học sinh lớp 7C được hay không ?

   Hướng dẫn giải

   a)

   – Số bạn nữ được biểu diễn bằng số thực (3; 5; 10; 4) nên nó là dữ liệu định lượng.

   – Khả năng đá bóng được biểu diễn bằng từ (không đạt, đạt, giỏi, xuất sắc) nên nó là dữ liệu định tính.

   b) Dữ liệu trên không đại diện được cho khả năng đá bóng của tất cả các bạn học sinh lớp 7C vì thiếu dữ liệu của các bạn học sinh nam.

   Bài 3: Tìm điểm chưa hợp lý của dữ liệu trong bảng sau

   

   Hướng dẫn giải

   Ta có: 40% + 20% + 15% + 35% = 110%

   Vậy điểm chưa hợp lý của dữ liệu trong bảng là tổng tỉ lệ phần trăm của các loại sách lớn hơn 100%.

   Bài 4: Hãy biểu diễn từ bảng thống kê sau đây vào biểu đồ

   

   

   Hướng dẫn giải

   Để biểu diễn dữ liệu từ bảng thống kê vào biểu đồ hình quạt trên ta thực hiện các bước sau:

   Bước 1: Xử lý số liệu:

   – Tính tổng các số liệu: 10 + 12 + 10 + 8 = 40.

   – Tính tỉ lệ phần trăm của từng số liệu so với toàn thể:

   $\frac{10}{40}=25\%$; $\frac{12}{40}=30\%$; $\frac{10}{40}=25\%$; $\frac{8}{40}=20\%$.

   Bước 2: Biểu diễn số liệu

   – Ghi tên biểu đồ: Tỉ lệ phần trăm các loại trái cây yêu thích của học sinh lớp 7B.

   – Ghi chú tên các đối tượng và các tỉ lệ phần trăm trên biểu đồ.

   Chuối: 25%; Xoài: 30%; Na: 25%; Bưởi 20%.

   

   Bài 5: Hãy phân tích biểu đồ sau:

   

   Hướng dẫn giải

   a) Biểu đồ trên biểu diễn thông tin về loại nước uống yêu thích của học sinh lớp 7A.

   b) Có bốn loại nước uống được học sinh chọn: nước cam, nước chanh, trà sữa, sinh tố.

   c) Trà sữa có tỉ lệ yêu thích cao nhất.

   d) Nước chanh có tỉ lệ yêu thích thấp nhất.

   e) Sinh tố và nước cam được học sinh yêu thích ngang nhau.

   Bài 6: Quan sát biểu đồ sau và trả lời câu hỏi:

   

   a) Biểu đồ biểu diễn các thông tin về vấn đề gì?

   b) Đơn vị thời gian là gì?

   c) Tháng nào cửa hàng có doanh thu cao nhất?

   d) Tháng nào cửa hàng có doanh thu thấp nhất?

   e) Doanh thu của cửa hàng tăng trong những khoảng thời gian nào?

   g) Doanh thu của cửa hàng giảm trong những khoảng thời gian nào?

   Hướng dẫn giải

   a) Biểu đồ biểu diễn các thông tin về: doanh thu trong 12 tháng của một cửa hàng A.

   b) Đơn vị thời gian là tháng.

   c) Tháng cửa hàng có doanh thu cao nhất là tháng 12 (80 triệu đồng).

   d) Tháng cửa hàng có doanh thu thấp nhất là tháng 1 (50 triệu đồng).

   e) Doanh thu của cửa hàng tăng trong những khoảng thời gian: từ tháng 1 đến tháng 4; từ tháng 5 đến tháng 8; từ tháng 10 đến tháng 12.

   g) Doanh thu của cửa hàng giảm trong những khoảng thời gian: tháng 4 – tháng 5; tháng 8 đến tháng 10.

   Bài 7: Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu của bảng thống kê sau:

   

   Hướng dẫn giải

   Bước 1: Vẽ hai thanh ngang và thẳng đứng vuông góc với nhau

   – Trục ngang: Ghi các mốc thời gian: tháng 9, tháng 10, tháng 11, tháng 12.

   – Trục thẳng đứng: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia.

   Bước 2:

   – Tại mỗi mốc chia thời gian trên trục ngang, đánh dấu một điểm cách mốc thời gian theo chiều thẳng đứng một khoảng bằng số liệu tại mốc thời gian đó, tương ứng với khoảng chia trên trục.

   – Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi của số liệu theo thời gian.

   

   Bước 3: Hoàn thiện biểu đồ

   – Ghi tên biểu đồ.

   – Ghi chú các giá trị số liệu tại các đầu đoạn thẳng.

   – Ghi đơn vị trên hai trục.

   

   Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

   Lý thuyết Bài 3: Biểu đồ đoạn thẳng

   Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê

   Lý thuyết Bài 1: Tỉ lệ thức – Dãy tỉ số bằng nhau

   Lý thuyết Bài 2: Đại lượng tỉ lệ thuận 

   Lý thuyết Bài 3: Đại lượng tỉ lệ nghịch
2. Lý thuyết Toán lớp 6 Chương 5 (Cánh diều 2023): Phân số và số thập phân hay, chi tiết
   Lý thuyết Toán lớp 6 Chương 5 : Phân số và số thập phân

   A. Lý thuyết Chương 5 : Phân số và số thập phân

   1. Phân số với tử số và mẫu số là số nguyên

   a) Khái niệm phân số

   Kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng $\frac{a}{b}.$

   Ta gọi $\frac{a}{b}$ là phân số.

   Phân số $\frac{a}{b}$ đọc là: a phần b, a là tử số (còn gọi tắt là tử), b là mẫu số (còn gọi tắt là mẫu).

   Chú ý: Mọi số nguyên a có thể viết dưới dạng phân số là $\frac{a}{1}.$ 

   b) Phân số bằng nhau

   Khái niệm hai phân số bằng nhau: Hai phân số được gọi là bằng nhau nếu chúng cùng biểu diễn một giá trị.

   Quy tắc bằng nhau của hai phân số:

   Xét hai phân số $\frac{a}{b}$ và $\frac{c}{d}$.

   Nếu $\frac{a}{b}=\frac{c}{d}$ thì a.d = b.c. Ngược lại, nếu a.d = b.c thì $\frac{a}{b}=\frac{c}{d}$.

   Chú ý: Với a, b là hai số nguyên và b ≠ 0, ta luôn có: $\frac{a}{-b}=\frac{-a}{b}$ và $\frac{-a}{-b}=\frac{a}{b}$.

   c) Tính chất cơ bản của phân số

   * Tính chất cơ bản

   – Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

   $\frac{a}{b}=\frac{a.m}{b.m}$ với $m\in \mathbb{Z}$, m ≠ 0.

   – Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

   $\frac{a}{b}=\frac{a:n}{b:n}$ với m $\in$ ƯC(a, b).

   Chú ý: Mỗi phân số đều đưa được về một phân số bằng nó và có mẫu là số dương.

   * Rút gọn về phân số tối giản

   Dựa vào tính chất cơ bản của phân số, để rút gọn phân số với tử và mẫu là số nguyên về phân số tối giản ta thường làm như sau:

   Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu “– “ (nếu có)

   Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất (ƯCLN) vừa tìm được, ta có phân số tối giản cần tìm.

   * Quy đồng mẫu nhiều phân số

   Để quy đồng nhiều phân số, ta thường làm như sau:

   Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm bội chung nhỏ nhất (BCNN) của các mẫu dương đó để làm mẫu số chung.

   Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu.

   Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.

   2. So sánh các phân số. Hỗn số dương

   a) So sánh các phân số

   * So sánh hai phân số

   Trong hai phân số khác nhau luôn có một phân số nhỏ hơn phân số kia.

   – Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}<\frac{c}{d}$ hay $\frac{c}{d}>\frac{a}{b}.$  

   – Phân số lớn hơn 0 gọi là phân số dương.

   – Phân số nhỏ hơn 0 gọi là phân số âm.

   – Nếu $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{e}{g}$ thì $\frac{a}{b}<\frac{e}{g}.$  

   * Cách so sánh hai phân số

   – So sánh hai phân số cùng mẫu

   Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.

   Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

   – So sánh hai phân số không cùng mẫu

   Để so sánh hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số đó (về cùng một mẫu dương) rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

   Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)

   Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

   b) Hỗn số dương

   Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

   3. Phép cộng, phép trừ phân số.

   a) Phép cộng phân số

   * Quy tắc cộng hai phân số

   – Quy tắc cộng hai phân số cùng mẫu

   Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.

   $\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$

   – Quy tắc cộng hai phân số không cùng mẫu

   Muốn cộng hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi cộng các tử và giữ nguyên mẫu chung.

   * Tính chất của phép cộng phân số

   Tương tự phép cộng các số tự nhiên, phép cộng phân số cũng có các tính chất: giao hoán, kết hợp, cộng với số 0.

   Trong thực hành, ta có thể sử dụng các tính chất này để tính giá trị biểu thức một cách hợp lí.

   b) Phép trừ phân số

   * Số đối của một phân số

   – Số đối của phân số $\frac{a}{b}$ kí hiệu là $-\frac{a}{b}$. Ta có: $\frac{a}{b}+\left(-\frac{a}{b}\right)=0$ 

   Chú ý: Ta có: $-\frac{a}{b}=\frac{a}{-b}=\frac{-a}{b}$ với $a,b\in \mathbb{Z},$ b ≠ 0.

   Số đối của $-\frac{a}{b}$ là $\frac{a}{b}$, tức là $-\left(-\frac{a}{b}\right)=\frac{a}{b}.$ 

   * Quy tắc trừ hai phân số

   – Muốn trừ hai phân số có cùng mẫu, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu.

   $\frac{a}{m}-\frac{b}{m}=\frac{a-b}{m}$.

   – Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu chung.

   – Muốn trừ hai phân số, ta cộng số bị trừ với số đối của số trừ:

   $\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left(-\frac{c}{d}\right).$

   c) Quy tắc dấu ngoặc

   – Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

   – Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”.

   $\frac{a}{b}-\left(\frac{c}{d}+\frac{e}{f}-\frac{g}{h}\right)=\frac{a}{b}-\frac{c}{d}-\frac{e}{f}+\frac{g}{h}$

   4. Phép nhân, phép chia phân số

   a) Phép nhân phân số

   * Quy tắc nhân hai phân số

   – Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

   $\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$ với b ≠ 0 và d ≠ 0.

   – Muốn nhân một số nguyên với một phân số (hoặc nhân một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu của phân số đó:

   $m.\frac{a}{b}=\frac{m.a}{b};\frac{a}{b}.n=\frac{a.n}{b}$ với b ≠ 0.

   * Tính chất của phép nhân phân số

   – Tính chất giao hoán: $\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{a}{b}$;

   – Tính chất kết hợp: $\left(\frac{a}{b}.\frac{c}{d}\right).\frac{p}{q}=\frac{a}{b}.\left(\frac{c}{d}.\frac{p}{q}\right)$;

   – Nhân với số 1” $\frac{a}{b}.1=1.\frac{a}{b}=\frac{a}{b}$;

   – Nhân với số 0: $\frac{a}{b}.0=0.\frac{a}{b}=0$;

   – Tính chất phân phối của phép nhân đối với phép cộng: $\frac{a}{b}.\left(\frac{c}{d}+\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}+\frac{a}{b}.\frac{p}{q}$;

   – Tính chất phân phối của phép nhân đối với phép trừ: $\frac{a}{b}.\left(\frac{c}{d}-\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}-\frac{a}{b}.\frac{p}{q}$.

   b) Phép chia phân số

   * Phân số nghịch đảo

   Phân số $\frac{b}{a}$ được gọi là phân số nghịch đảo của phân số $\frac{a}{b}$ với a ≠ 0 và b ≠ 0.

   Chú ý: Tích của một phân số với phân số nghịch đảo của nó thì bằng 1.

   * Phép chia phân số

   Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia:

   $\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}=\frac{a.d}{b.c}$ với b, c, d khác 0.

   c) Thứ tự thực hiện phép tính với phân số:

   * Thứ tự thực hiện phép tính với phân số trong biểu thức không chứa dấu ngoặc:

   Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

   * Thứ tự thực hiện phép tính với phân số trong biểu thức có chứa dấu ngoặc:

   Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

   5. Số thập phân

   a) Số thập phân

   – Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

   – Phân số thập phân có thể viết được dưới dạng số thập phân.

   – Số thập phân gồm hai phần:

   + Phần số nguyên được viết bên trái dấu phẩy;

   + Phần thập phân được viết bên phải dấu phẩy.

   b) So sánh các số thập phân

   * So sánh hai số thập phân

   Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

   – Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

   – Số thập phân lớn hơn 0 gọi là số thập phân dương.

   – Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

   – Nếu a < b và b < c thì a < c.

   * Cách so sánh hai số thập phân

   – So sánh hai số thập phân khác dấu:

   Số thập phân âm luôn nhỏ hơn số thập phân dương.

   – So sánh hai số thập phân dương:

   Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

   Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

   – So sánh hai số thập phân âm:

   Nếu a < b thì ‒ a > ‒ b.

   6. Phép cộng, phép trừ số thập phân

   a) Số đối của số thập phân

   Số đối của số thập phân a kí hiệu là ‒a. Ta có: a + (‒a) = 0.

   Chú ý: Số đối của số thập phân ‒a là a, tức là ‒(‒a) = a.

   b) Phép cộng, phép trừ số thập phân

   * Cộng hai số thập phân

   – Cộng hai số thập phân dương: Muốn cộng hai số thập phân dương ta thực hiện quy tắc cộng hai số nguyên dương.

   – Cộng hai số thập phân âm: Muốn cộng hai số thập phân âm ta cộng hai số đối của chúng rồi thêm dấu “‒” đằng trước kết quả:

   (‒a) + (‒b) = ‒(a + b)

   – Cộng hai số thập phân khác dấu, ta làm như sau:

    + Nếu số dương lớn hơn hay bằng số đối của số âm thì lấy số dương trừ đi số đối của số âm.

    + Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ “‒” trước kết quả.

   – Tính chất của phép cộng số thập phân:

   Giống như phép cộng số nguyên, phép cộng số thập phân có các tính chất giao hoán, kết hợp, cộng với số 0, cộng với số đối.

   * Trừ hai số thập phân

   – Muốn trừ hai số thập phân, ta cộng số bị trừ với số đối của số trừ.

   a – b = a + (–b)

   c) Quy tắc dấu ngoặc

   – Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

   – Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”:

   a ‒ (b + c – d) = a ‒ b ‒ c + d

   7. Phép nhân, phép chia số thập phân

   a) Phép nhân số thập phân

   * Nhân hai số thập phân

   Muốn nhân hai số thập phân dương, ta làm như sau:

   Bước 1: Viết thừa số này ở dưới thừa số kia như đối với phép nhân các số tự nhiên

   Bước 2: Thực hiện phép nhân như nhân số tự nhiên

   Bước 3: Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu “,”  tách ở tích ra bấy nhiêu chữ số từ phải sang trái, ta nhận được tích cần tìm.

   Chú ý: Hai số thập phân cùng dấu thì tích là số dương; hai số thập phân khác dấu thì tích là số âm.

   Nhân hai số thập phân cùng dấu: (‒a) . (‒b) = a.b với a, b > 0

   Nhân hai số thập phân khác dấu: (‒a) . b = a.(‒b) = ‒ (a.b) với a, b > 0

   * Tính chất của phép nhân số thập phân

   Phép nhân số thập phân cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân với phép cộng và phép trừ.

   b) Phép chia số thập phân

   Muốn chia hai số thập phân dương, ta làm như sau:

   Bước 1: Số chia có bao nhiêu chữ số sau dấu “,” thì chuyển dấu “,”  ở số bị chia sang bên phải bấy nhiêu chữ số. (Khi chuyển dấu “,” ở số bị chia sang phải mà số bị chia không đủ vị trí, thì ta điền thêm những chữ số 0 vào bên phải của số đó)

   Bước 2: Bỏ đi dấu “,” ở số chia, ta nhận được số nguyên dương

   Bước 3: Đem số nhận được ở Bước 1 chia cho số nguyên dương nhận được ở Bước 2, ta có thương cần tìm.

   Chú ý: Hai số thập phân cùng dấu thì thương là số dương; hai số thập phân khác dấu thì thương là số âm.

   Chia hai số thập phân cùng dấu: (‒a) : (‒b) = a : b với a, b > 0

   Chia hai số thập phân khác dấu: (‒a) : b = a : (‒b) = ‒ (a : b) với a, b > 0

   c) Thứ tự thực hiện phép tính với số thập phân:

   * Thứ tự thực hiện phép tính với số thập phân trong biểu thức không chứa dấu ngoặc:

   Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

   * Thứ tự thực hiện phép tính với số thập phân trong biểu thức có chứa dấu ngoặc:

   Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

   8. Ước lượng và làm tròn số

   a) Làm tròn số nguyên

   Để làm tròn một số nguyên (có nhiều chữ số) đến một hàng nào đó, ta làm như sau:

   – Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

   – Nếu chữ số đứng ngày bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số của hàng làm tròn rồi thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

   Chú ý: Kí hiệu “≈” đọc là “gần bằng” hoặc “xấp xỉ”.

   b) Làm tròn số thập phân

   Để làm tròn một số thập phân dương đến một hàng nào đó (gọi là hàng làm tròn), ta làm như sau:

   – Tìm chữ số hàng làm tròn

   – Nhìn sang chữ số ngay bên phải

   + Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số hàng làm tròn và thay tất cả các chữ số bên phải bằng số 0 và bỏ đi nếu chúng ở phần thập phân.

   + Nếu chữ số đó lớn hơn hay bằng 5 thì tăng chữ số hàng làm tròn thêm 1 rồi thay tất cả các chữ số bên phải bằng 0 hoặc bỏ đi nếu chũng ở phấn thập phân.

   c) Ước lượng kết quả các phép tính

   Để ước lượng kết quả các phép tính ta thực hiện làm tròn các số trong phép tính.

   9. Tỉ số. Tỉ số phần trăm

   a)Tỉ số

   * Tỉ số của hai số

   Tỉ số của a và b (b ≠ 0) là thương trong phép chia số a cho số b, kí hiệu là a : b hoặc $\frac{a}{b}$.

   Chú ý:

   – Nếu tỉ số của a và b được viết dưới dạng $\frac{a}{b}$ thì ta cũng gọi a là tử số và b là mẫu số.

   – Tỉ số của số a và số b phải được viết theo đúng thứ tự là $\frac{a}{b}$ hoặc a : b.

   – Tỉ số $\frac{a}{b}$ là phân số nếu cả tử a và mẫu b đều là số nguyên.

   * Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo)

   Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số giữa hai số đo của hai đại lượng đó.

   Nhận xét: Tỉ số của hai đại lượng thể hiện độ lớn của đai lượng này so với đại lượng kia.

   a : b = $2\frac{3}{5}:\frac{9}{10}=\frac{13}{5}.\frac{10}{9}=\frac{26}{9}$.

   b) Tỉ số phần trăm

   * Tỉ số phần trăm của hai số

   – Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$.

   – Để tính tỉ số phần trăm của a và b, ta làm như sau:

   + Bước 1: Viết tỉ số $\frac{a}{b}$ 

   + Bước 2: Tính số $\frac{a.100}{b}$ và viết thêm % vào bên phải số vừa nhận được.

   Nhận xét: Có hai cách tính $\frac{a.100}{b}$ là:

   – Chia a cho b để tìm thương (ở dạng số thập phân) rồi lấy thương đó nhân với 100.

   – Nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

   Chú ý: Khi tính tỉ số phần trăm của a và b mà phải làm tròn số thập phân thì ta kàn theo cách nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

   * Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo)

   Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số phần trăm giữa hai số đo của hai đại lượng đó.

   Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là: $\frac{a.100}{b}\%$.

   10. Bài toán về hai phân số

   a) Tìm giá trị phân số của một số cho trước

   – Muốn tìm giá trị $\frac{m}{n}$ của số a cho trước, ta tính $a.\frac{m}{n}$ $\left(m\in \mathbb{N},n\in \mathbb{N}*\right)$ .

   Giá trị của m% của số a là giá trị phân số $\frac{m}{100}$ của số 

   – Muốn tìm giá trị m% của số a cho trước, ta tính $a.\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

   b) Tìm một số biết giá trị phân số của số đó

   – Muốn tìm một số biết $\frac{m}{n}$ của nó bằng a, ta tính $a:\frac{m}{n}\left(m,n\in \mathbb{N}*\right)$.

   – Muốn tìm một số biết m% của nó bằng a, ta tính $a:\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

   B. Bài tập tự luyện

   Bài 1. Tìm số nguyên x, biết:

   a) $\frac{3}{x}=\frac{-18}{24}$;

   b) $\frac{25}{30}=\frac{2x+3}{6}$ 

   Hướng dẫn giải

   a) Vì $\frac{3}{x}=\frac{-18}{24}$

   Suy ra 3.24 = x. (–18)

   x. (–18) = 3.24

   x. (–18) = 72

   x = 72 :  (–18)

   x = –4.

   Vậy x = –4.

   b) $\frac{25}{30}=\frac{2x+3}{6}$ 

   Suy ra 30.(2x + 3) = 25.6

   30.2x + 30.3 = 150

   60x + 90 = 150

   60x = 150 – 90

   60x = 60

   x = 60 : 60

   x = 1.

   Vậy x = 1.

   Bài 2. Sắp xếp các số sau theo thứ tự tăng dần: $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$

   Hướng dấn giải

   Ta chia các số $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$ thành hai nhóm:

   Nhóm 1: gồm các số $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Nhóm 2: gồm các số $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

   Ta đi so sánh nhóm 1: $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Có  $\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$; $\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$  và $1\frac{1}{2}=1+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}=\frac{3.6}{2.6}=\frac{18}{12}.$  

   Do 9 < 10 < 18 nên $\frac{9}{12}<\frac{10}{12}<\frac{18}{12}$ 

   Vậy $\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$ 

   Ta đi so sánh nhóm 2: $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

   Vì $\frac{2}{9}<\frac{5}{9}<\frac{5}{8}$ nên $-\frac{2}{9}>-\frac{5}{8}$

   Vì $\frac{2}{9}>\frac{2}{12}>\frac{1}{12}$ nên $-\frac{2}{9}<-\frac{1}{12}$

   Do đó $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}$

   Trong tất cả các phân số thì phân số âm luôn nhỏ hơn phân số dương, do đó ta có:

   $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}<\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$

   Vậy ta có thể sắp xếp theo thứ tự tăng dần là $-\frac{5}{8};-\frac{2}{9};-\frac{1}{12};\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Bài 3. Viết các đại lượng sau dưới dạng phân số và so sánh:

   a) Thời gian nào dài hơn: 2 giờ 45 phút hay $2\frac{1}{4}$ giờ?      

   b) Vận tốc nào nhỏ hơn: $\frac{5}{6}$ km/h hay $\frac{7}{9}$ km/h?

   Hướng dẫn giải

   a) Ta có 45 phút = $\frac{45}{60}$ giờ = $\frac{45:15}{60:15}$ giờ = $\frac{3}{4}$ giờ

   Do đó 2 giờ 45 phút = $\left(2+\frac{3}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{3}{4}\right)$ giờ = $\frac{11}{4}$ giờ.

   $2\frac{1}{4}$ giờ = $\left(2+\frac{1}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{1}{4}\right)$ giờ = $\frac{9}{4}$ giờ.

   Vì 11 > 9 nên $\frac{11}{4}>\frac{9}{4}$

   Do đó 2 giờ 45 phút > $2\frac{1}{4}$ giờ.

   Vậy 2 giờ 45 phút dài hơn  giờ.

   b) Ta có  $\frac{7}{9}=\frac{7.6}{9.6}=\frac{42}{54}$  và $\frac{5}{6}=\frac{5.9}{6.9}=\frac{45}{54}$

   Vì 42 < 45 nên $\frac{42}{54}<\frac{45}{54}$        

   Do đó $\frac{7}{9}$ km/h < $\frac{5}{6}$ km/h

   Vậy vận tốc $\frac{7}{9}$ km/h nhỏ hơn $\frac{5}{6}$ km/h.

   Bài 4. Tính:

   a) $\frac{6}{13}+\frac{-15}{39}$

   b) $\frac{-18}{24}+\frac{15}{21}$

   c) $\frac{1}{6}-\frac{5}{6}$

   d) $\frac{7}{21}-\frac{9}{-36}$

   Hướng dẫn giải

   a) $\frac{6}{13}+\frac{-15}{39}=\frac{6}{13}+\frac{\left(-15\right):3}{39:3}=\frac{6}{13}+\frac{-5}{13}=\frac{6+\left(-5\right)}{13}=\frac{1}{13}$

   b) $\frac{-18}{24}+\frac{15}{21}=\frac{\left(-18\right):6}{24:6}+\frac{15:3}{21:3}=\frac{-3}{4}+\frac{5}{7}$

   $=\frac{\left(-3\right).7}{4.7}+\frac{5.4}{7.4}=\frac{-21}{28}+\frac{20}{28}=\frac{\left(-21\right)+20}{28}=\frac{-1}{28}$                   

   c) $\frac{1}{6}-\frac{5}{6}=\frac{1-5}{6}=\frac{1+\left(-5\right)}{6}=\frac{-4}{6}=\frac{\left(-4\right):2}{6:2}=\frac{-2}{3}$

   d) $\frac{7}{21}-\frac{9}{-36}=\frac{7:7}{21:7}-\frac{-9}{36}=\frac{1}{3}+\left(-\frac{-9}{36}\right)=\frac{1}{3}+\frac{9}{36}$

   $=\frac{1}{3}+\frac{9:9}{36:9}=\frac{1}{3}+\frac{1}{4}=\frac{1.4}{3.4}+\frac{1.3}{4.3}$

   $=\frac{4}{12}+\frac{3}{12}=\frac{4+3}{12}=\frac{7}{12}$

   Bài 5. Tính một cách hợp lí:

   a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

   b)$B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

   c)$C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

   Hướng dẫn giải

   a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

   $=\frac{-5}{7}+\frac{-2}{7}+\frac{3}{4}+\frac{1}{4}+\frac{-1}{5}$

    $=\left(\frac{-5}{7}+\frac{-2}{7}\right)+\left(\frac{3}{4}+\frac{1}{4}\right)+\frac{-1}{5}$    

   $=\frac{\left(-5\right)+\left(-2\right)}{7}+\frac{3+1}{4}+\frac{-1}{5}$

   $=\frac{-7}{7}+\frac{4}{4}+\frac{-1}{5}$

    $=-1+1+\frac{-1}{5}$  

   $=0+\frac{-1}{5}$

   $=\frac{-1}{5}$

   Vậy $A=\frac{-1}{5}$.

   b) $B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

   $=\frac{-3}{31}+\frac{-28}{31}-\frac{6}{17}+\frac{-11}{17}-\frac{-1}{25}-\frac{1}{5}$

   $=\left(\frac{-3}{31}+\frac{-28}{31}\right)+\left(-\frac{6}{17}+\frac{-11}{17}\right)+\left(-\frac{-1}{25}-\frac{1}{5}\right)$ 

   $=\frac{\left(-3\right)+\left(-28\right)}{31}+\frac{\left(-6\right)+\left(-11\right)}{17}+\left(\frac{1}{25}-\frac{5}{25}\right)$

   $=\frac{-31}{31}+\frac{-17}{17}+\frac{1-5}{25}$

   $=\left(-1\right)+\left(-1\right)+\frac{-4}{25}$

   $=-2+\frac{-4}{25}$

   $=\frac{-50}{25}+\frac{-4}{25}$

   $=\frac{-50+\left(-4\right)}{25}$

   $=\frac{-54}{25}.$

   Vậy $B=\frac{-54}{25}.$

   c) $C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

   $=\frac{-5}{21}-\frac{16}{21}+1$

   $=\left(\frac{-5}{21}-\frac{16}{21}\right)+1$

   $=\frac{-5-16}{21}+1$

   $=\frac{\left(-5\right)+\left(-16\right)}{21}+1$

   $=\frac{-21}{21}+1$

   = (‒1) + 1

   = 0.

   Vậy C = 0.

   Bài 6. Hai người cùng làm chung một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai phải mất 7 giờ mới xong công việc. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần công việc?

   Hướng dẫn giải:

   Coi toàn bộ công việc là  đơn vị.

   Người thứ nhất làm xong công việc trong  giờ. Suy ra trong  giờ thì người thứ nhất làm được $\frac{1}{4}$ công việc.

   Người thứ hai làm xong công việc trong  giờ. Suy ra trong  giờ người thứ hai làm được $\frac{1}{7}$ công việc.

   Do đó trong  giờ, cả hai cùng làm thì được số phần công việc là:

   $\frac{1}{4}+\frac{1}{7}=\frac{1.7}{4.7}+\frac{1.4}{7.4}=\frac{7}{28}+\frac{4}{28}=\frac{7+4}{28}=\frac{11}{28}$ (công việc).

   Vậy nếu làm chung thì mỗi giờ cả hai người làm được $\frac{11}{28}$ công việc.

   Bài 7. Chị An sau khi tốt nghiệp đại học và đi làm, chị nhận được tháng lương đầu tiên. Chị quyết định dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình và $\frac{1}{3}$ số tiền để mua quà tặng bố mẹ, số tiền còn lại chị để tiết kiệm. Số phần tiền để tiết kiệm của chị An là bao nhiêu?

   Hướng dẫn giải

   Coi toàn bộ số tiền lương thág đầu tiên của chị An là 1 đơn vị.

   Số tiền còn lại sau khi chị dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình là:

   $1-\frac{3}{5}=\frac{5}{5}-\frac{3}{5}=\frac{5-3}{5}=\frac{2}{5}$ (số tiền)

   Số tiền để tiết kiệm của chị An là:

   $\frac{2}{5}-\frac{1}{3}=\frac{2.3}{5.3}-\frac{1.5}{3.5}=\frac{6}{15}-\frac{5}{15}=\frac{6-5}{15}=\frac{1}{15}$ (số tiền)

   Vậy số phần tiền  để tiết kiệm của chị An là $\frac{1}{15}$.

   Bài 8. Tính giá trị biểu thức (tính hợp lí nếu có thể):

   a) $\left(\frac{3}{-10}\right)\left(-\frac{-15}{2}\right)$;

   b) $\frac{-4}{7}:\frac{-1}{3};$

   c) $\frac{4}{5}+\frac{3}{5}:3-\frac{7}{8};$

   d) $\left(-\frac{5}{24}+\frac{3}{2^2}+\frac{7}{12}\right):2\frac{1}{8}$

   e) $\frac{6}{7}.\frac{8}{13}+\frac{6}{13}.\frac{9}{7}-\frac{4}{13}.\frac{6}{7}$

   Hướng dẫn giải

   a) $\left(\frac{3}{-10}\right)\left(-\frac{-15}{2}\right)=\frac{3}{-10}.\frac{15}{2}=\frac{3.15}{\left(-10\right).2}$

   $=\frac{\mathrm{3.3.5}}{\left(-2\right)\mathrm{.5.2}}=\frac{3.3}{\left(-2\right).2}=\frac{9}{-4}$;

   b) $\frac{-4}{7}:\frac{-1}{3}=\frac{-4}{7}.\frac{3}{-1}=\frac{\left(-4\right).3}{7.\left(-1\right)}=\frac{-12}{-7}=\frac{12}{7};$

   c) $\frac{4}{5}+\frac{3}{5}:3-\frac{7}{8}=\frac{4}{5}+\frac{3}{5}.\frac{1}{3}-\frac{7}{8}$

    $=\frac{4}{5}+\frac{3.1}{5.3}-\frac{7}{8}=\frac{4}{5}+\frac{1}{5}-\frac{7}{8}$  

   $=\frac{5}{5}-\frac{7}{8}$$=1-\frac{7}{8}$

   $=\frac{8}{8}-\frac{7}{8}$$=\frac{1}{8}$;

   d) $=\frac{9}{8}.\frac{8}{17}$$\left(-\frac{5}{24}+\frac{3}{2^2}+\frac{7}{12}\right):2\frac{1}{8}$

   $=\left(-\frac{5}{24}+\frac{3}{4}+\frac{7}{12}\right):\frac{17}{8}$

   $=\left(-\frac{5}{24}+\frac{18}{24}+\frac{14}{24}\right):\frac{17}{8}$

   $=\frac{-5+18+14}{24}:\frac{17}{8}$

   $=\frac{9.8}{8.17}$

   $=\frac{9}{17}$;

   e) $\frac{6}{7}.\frac{8}{13}+\frac{6}{13}.\frac{9}{7}-\frac{4}{13}.\frac{6}{7}$

   $=\frac{6}{7}.\frac{8}{13}+\frac{6}{7}.\frac{9}{13}-\frac{6}{7}.\frac{4}{13}$

   $=\frac{6}{7}.\left(\frac{8}{13}+\frac{9}{13}-\frac{4}{13}\right)$

   $=\frac{6}{7}.\frac{8+9-4}{13}$

   $=\frac{6}{7}.\frac{13}{13}$

   $=\frac{6}{7}.1$

   $=\frac{6}{7}$.

   Bài 9. Tìm x, biết:

   a) $\frac{2}{9}-\frac{7}{8}.x=1;$

   b) $\frac{5}{7}:x-1=\frac{2}{3}$;

   c) $\left(4\frac{1}{2}-2x\right).1\frac{4}{61}=6\frac{1}{2}$

   Hướng dẫn giải

   a) $\frac{2}{9}-\frac{7}{8}.x=1$

   $\frac{7}{8}.x=\frac{2}{9}-1$

   $\frac{7}{8}.x=\frac{2}{9}-\frac{9}{9}$

   $\frac{7}{8}.x=\frac{-7}{9}$

   $x=\frac{-7}{9}:\frac{7}{8}$

   $x=\frac{-7}{9}.\frac{8}{7}$

   $x=\frac{\left(-7\right).8}{9.7}$

   $x=\frac{\left(-1\right)\mathrm{.7.8}}{9.7}$

   $x=\frac{-8}{9}$

   Vậy $x=\frac{-8}{9}$

   b) $\frac{5}{7}:x-1=\frac{2}{3}$

   $\frac{5}{7}:x=\frac{2}{3}+1$

   $\frac{5}{7}:x=\frac{2}{3}+\frac{3}{3}$

   $\frac{5}{7}:x=\frac{5}{3}$

   $x=\frac{5}{7}:\frac{5}{3}$

   $x=\frac{5}{7}.\frac{3}{5}$

   $x=\frac{3}{7}.$

   Vậy $x=\frac{3}{7}.$

   c) $\left(4\frac{1}{2}-2x\right).1\frac{4}{61}=6\frac{1}{2}$

   $\left(\frac{9}{2}-2x\right).\frac{65}{61}=\frac{13}{2}$

   $\frac{9}{2}-2x=\frac{13}{2}:\frac{65}{61}$

   $\frac{9}{2}-2x=\frac{13}{2}.\frac{61}{65}$

   $\frac{9}{2}-2x=\frac{13}{2}.\frac{61}{5.13}$

   $\frac{9}{2}-2x=\frac{61}{10}$

   $2x=\frac{9}{2}-\frac{61}{10}$

   $2x=\frac{45}{10}-\frac{61}{10}$

   $2x=\frac{-16}{10}$

   $2x=\frac{-8}{5}$

   $x=\frac{-8}{5}:2$

   $x=\frac{-8}{5}.\frac{1}{2}$

   $x=\frac{-4}{5}$

   Vậy $x=\frac{-4}{5}$.

   Bài 10. Sau một thời gian gửi tiết kiệm với số tiền là 8 triệu đồng, người gửi đi rút tiền và nhận số tiền lãi bằng $\frac{1}{25}$ số tiền gửi tiết kiệm. Hỏi sau khi rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?

   Hướng dẫn giải

   Vì số tiền lãi bằng $\frac{1}{25}$ số tiền gửi tiết kiệm nên số tiền lãi người đó nhận được là:

   $8 000 000.\frac{1}{25}=320 000$(đồng).

   Tổng số tiền người đó nhận được là:

   8 000 000 + 320 000 = 8 320 000 (đồng)

   Vậy tổng số tiền người đó nhận được là 8 320 000 đồng.

   Bài 11. Cho các phân số và hỗn số: $\frac{-3}{10}$; $\frac{7}{-50};$$1\frac{19}{125};$ $\frac{27}{{10}^3}$; $\frac{7}{8}.$  

   a) Viết các phân số và hỗn số trên dưới dạng phân số thập phân;

   b) Sắp xếp các số thập phân tìm được ở câu a theo thứ tự tăng dần.

   Hướng dẫn giải

   a) Ta có: $\frac{-3}{10}=-\frac{3}{10}=-0,3$;

   $\frac{7}{-50}=-\frac{7}{50}=-\frac{7.2}{50.2}=-\frac{14}{100}=-0,14$

   $1\frac{19}{125}=1+\frac{19}{125}=\frac{125}{125}+\frac{19}{125}=\frac{144}{125}=\frac{144.8}{125.8}=\frac{1152}{1000}=1,152;$

   $\frac{27}{{10}^3}=\frac{27}{1000}=0,027$

   $\frac{7}{8}=\frac{7.125}{8.125}=\frac{875}{1000}=0,875$

   Vậy $\frac{-3}{10}=-0,3;\frac{7}{-50}=-0,14;1\frac{19}{125}=1,152;\frac{27}{{10}^3}=0,027;\frac{7}{8}=0,875$

   b) Ta chia các số ‒0,3; ‒0,14; 1,152; 0,027; 0,875 thành hai nhóm:

   Nhóm 1 gồm các số: ‒0,3; ‒0,14

   Nhóm 2 gồm các số 1,152; 0,027; 0,875.

   Ta đi so sánh nhóm 1: ‒0,3; ‒0,14

   Xét hai số 0,3 và 0,14: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 3 > 1 nên 0,3 > 0,14 do đó ‒0,3 < ‒0,14.

   Ta đi so sánh nhóm 2: 1,152; 0,027; 0,875.

   Xét hai số 0,027 và 0,875: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số này là hàng phần mười. Mà 0 < 8 nên 0,027 < 0,875.

   Xét hai số 0,875 và 1,152: Ta thấy phần nguyên của hai số là 0 < 1 nên 0,875 < 1,152.

   Suy ra 0,027 < 0,875 < 1,152

   Nhóm 1 gồm các số âm và nhóm 2 gồm các số dương. Mà số âm luôn nhỏ hơn số dương.

   Do đó ta có ‒0,3 < ‒0,14 < 0,027 < 0,875 < 1,152.

   Vậy sắp xếp các số thập phân theo thứ tự tăng dần là  ‒0,3; ‒0,14; 0,027; 0,875; 1,152.

   Bài 12. Biết nhiệt độ đông đặc của thuỷ ngân là ‒38,83°C, của rượu là ‒114,1°C, của băng phiến là 80,26°C và của nước là 0°C.

   Hãy cho biết nhiệt độ đông đặc của chất nào là thấp nhất?

   Hướng dẫn giải

   Ta so sánh hai số ‒38,83 và ‒114,1:

   Xét hai số 38,83 và 114,1 ta thấy phần nguyên của hai số là 38 < 114 nên 38,83 < 114,1 suy ra ‒38,83 > ‒114,1

   Ta thấy nhiệt độ đông đặc của thuỷ ngân (‒38,83°C) và của rượu (‒114,1°C) là số thập phân âm; nhiệt độ đông đặc của băng phiến (80,26°C ) là số thập phân dương và của nước là số 0.

   Mà số 0 luôn lớn hơn số thập phân âm và nhỏ hơn số thập phân dương.

   Do đó ta có: ‒114,1 < ‒38,83  < 0 < 80,26

   Hay ‒114,1°C < ‒38,83°C < 0°C < 80,26°C.

   Vậy nhiệt độ đông đặc của rượu là thấp nhất.

   Bài 13. Tính một cách hợp lí:

   a) A = 41,54 – 3,18 + 23,17 + 8,46 – 5,82 – 3,17

   b) B = 32,18 + 36,42 – 13,93 – (2,18 + 6,42 – 3,93)

   Hướng dẫn giải

   a) A = 41,54 – 3,18 + 23,17 + 8,46 – 5,82 – 3,17

   A = 41,54 + 8,46 + 23,17 – 3,17 – 3,18 – 5,82

   A = (41,54 + 8,46) + (23,17 – 3,17) – (3,18 + 5,82)

   A = 50 + 20 – 9

   A = 70 – 9

   A = 61.

   b) B = 32,18 + 36,42 – 13,93 – (2,18 + 6,42 – 3,93)

   B = 32,18 + 36,42 – 13,93 – 2,18 – 6,42 + 3,93

   B = (32,18 – 2,18) + (36,42 – 6,42) – (13,93 ‒ 3,93)

   B = 30 + 30 – 10

   B = 60 – 10

   B = 50.

   Bài 14. Tính (tính hợp lí nếu có thể):

   a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$;

   b) 5,34 . 26,15 + 5,34 . (‒126,15).

   Hướng dẫn giải

   a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$   

   $=-\frac{1}{13}.\left(\frac{13}{4}-\frac{65}{10}\right):\frac{2}{5}+\left[-\left(0,246:3\right)\right]$

   $=-\frac{1}{13}.\left(\frac{13}{4}-\frac{13}{5}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{13}\mathrm{.13.}\left(\frac{1}{4}-\frac{1}{5}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{1}\mathrm{.1.}\left(\frac{5}{20}-\frac{4}{20}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{20}.\frac{5}{2}+\left(-0,082\right)$

   $=-\frac{1}{4.5}.\frac{5}{2}+\left(-0,082\right)$

   $=-\frac{1}{8}+\left(-0,082\right)$

   = ‒ 0,125 + (‒0,082)

   = ‒ (0,125 + 0,082)

   = ‒ 0,207.

   b) 5,34 . 26,15 + 5,34 . (‒126,15)

   = 5,34 . [26,15 + (‒126,15)]

   = 5,34 . [‒ (126,15 – 26,15)]

   = 5,34 . (‒100)

   = ‒ (5,34 . 100)

   = ‒ 534.

   Bài 15. Mức tiêu thụ nhiên liệu của một chiếc xe máy Honda SH mode là 1,9 lít trên 100 ki – lô – mét. Giá một lít xăng E5 RON 95 – II ngày 11/04/2022 là 27 309 đồng. Một người đi xe máy đó trên quãng đường 100 km thì sẽ hết bao nhiêu tiền xăng?

   Hướng dấn giải

   Số tiền xăng người đi xe máy đi hết quãng đường 100 km là:

   27 309 . 1,9 = 51 887,1 (đồng)

   Vậy để đi được quãng đường 100 km thì người đó hết 51 887,1 đồng tiền xăng.

   Bài 16. Một khu đất hình chữ nhật có chiều dài 31,23 m và chiều rộng bằng $\frac{2}{3}$ chiều dài.

   a) Người ta lấy $\frac{5}{6}$ diện tích khu đất để đào ao. Tính diện tích ao.

   b) Diện tích còn lại người ta trồng rau. Biết cứ 1 m² thì thu hoạch được 2,1 kg rau. Hỏi người ta thu hoạch được bao nhiêu kg rau?

   c) Mỗi ki – lô – gam rau người đó bán được 12 000 đồng. Vậy nếu bán hết số rau thu hoạch được thì người đó bán được bao nhiêu tiền?

   Hướng dẫn giải

   Chiều rộng khu đất hình chữ nhật là: 31,23 . $\frac{2}{3}$ = 20,82 (m)

   Diện tích khu đất hình chữ nhật là: 31,23 . 20,82 = 650,2086 (m²)

   a) Diện tích người đó dùng để đào ao là: 650,2086 . $\frac{5}{6}$ = 541,8405 (m²).

   b) Diện tích còn lại dùng để trồng rau là: 650,2086 – 541,8405 = 108,3681 (m²)

   Số kg rau người đó thu hoạch được là: 108,3681 . 2,1 = 227, 57301 (kg).

   c) Số tiền người đó bán rau thu được là: 227,57301 . 12 000 = 2 730 876,12 (đồng).

   Bài 17. Một căn phòng hình hộp chữ nhật với chiều dài 3,8 m, chiều rộng 3,2 m và chiều cao 3 m. Người ta muốn sơn trần nhà và bốn bức tường bên trong phòng.

   a) Tính diện tích cần sơn biết tổng diện tích các cửa là 4,5 m².

   b) Biết giá tiền công sơn tường và trần nhà đều là 15 000 đồng. Tính tổng số tiền công sơn căn phòng đó.

   Hướng dẫn giải

   a) Diện tích trần nhà của căn phòng là: 3,8. 3,2 = 12,16 (m²).

   Diện tích bốn bức tường của căn phòng là: 2.(3,8 + 3,2). 3 = 42 (m²)

   Diện tích trần nhà và bốn bức tường căn phòng hình hộp chữ nhật là:

   12,16 + 42 = 54,16 (m²).

   Diện tích cần sơn là: 54,16 – 4,5 = 49,66 (m²).

   Vậy diện tích cần sơn là: 49,66 (m²).

   b) Số tiền công sơn căn phòng là:

   49,66 . 15 000 = 744 900 (đồng).

   Vậy số tiền công sơn căn phòng là 744 900 đồng.

   Bài 18. Theo https://ourworldindata.org/covid-vaccinations?country=VNM , tính đến ngày  21/03/2022, số người dân Việt Nam đã tiêm ít nhất một liều vaccine là 79 701 388 người. Sử dụng số thập phân để viết số người Việt Nam theo đơn vị triệu người. Sau đó làm tròn số thập phân đó đến:

   a) Hàng phần mười

   b) Hàng phần trăm.

   Hướng dẫn giải

   Tính đến ngày 21/03/2022, số người dân Việt Nam đã được tiêm ít nhất một liều vaccine là 79,701388 triệu người.

   a) Làm tròn số 79,701388 đến hàng phần mười:

   Do chữ số hàng phần trăm của số 79,701388 là 0 < 5 nên 79,701388 ≈ 79,7.

   Vậy số người dân Việt Nam đã được tiêm ít nhất một liều vaccine xấp xỉ 79,7 triệu người.

   b) Làm tròn số 79,701388 đến hàng phần trăm:

   Do chữ số hàng phần nghìn của số 79,701388 là 1 < 5 nên 79,701388 ≈ 79,7.

   Vậy số người dân Việt Nam đã được tiêm ít nhất một liều vaccine xấp xỉ 79,7 triệu người.

   Bài 19. Một chiếc xe máy chuyển động trên quãng đường từ Hà Nội đến Hải Phòng là 120 km. Bánh xe của chiếc xe máy có dạng hình tròn có đường kính 43 cm. Hỏi trong quá trình di chuyển từ Hà Nội đến Hải Phòng thì bánh xe quay được bao nhiêu vòng? Làm tròn kết quả đến hàng đơn vị và lấy π = 3,14.

   Hướng dẫn giải

   Đổi 120 km = 120 000 m.

   43 cm = 0,43 m.

   Chu vi của bánh xe là: C = π.d = 3,14. 0,43 = 1,3502 (m).

   Số vòng quay mà bánh xe quay được là: 120 000 : 1,3502 = 88 875,72211… (vòng)

   Làm tròn kết quả trên đến hàng đơn vị: do chữ số hàng phần mười của kết quả là 7 > 5 nên 88 875,72211…≈ 88 876.

   Vậy trong quá trình di chuyển từ Hà Nội đến Hải Phòng thì bánh xe máy quay được khoảng 88 876 vòng.

   Bài 20. Mẹ Hoa đưa cho Hoa tờ tiền 500 000 đồng để Hoa mang đi mua thức ăn cho mèo. Người bán hàng nói chỉ còn 2,45 kg thức ăn cuối cùng bán với giá 190 000 đồng một kg. Hãy ước lượng xem số tiền Hoa mang theo có đủ mua hết số thức ăn đó không?

   Hướng dẫn giải

   Hoa cần ước lượng 2,46 ≈ 2,5 kg và 190 000 ≈ 200 000.

   Sau đó thực hiện phép tính nhân: 2,5 . 200 000 = 500 000 (đồng).

   Do cả hai thừa số đều được làm tròn tăng lên nên tích đúng sẽ nhỏ hơn tích mà Hoa đã ước lượng. Vì vậy số tiền 500 000 đồng mà Hoa mang đi sẽ trả đủ cho 2,45 kg thức ăn cho mèo.

   Bài 21. Ước lượng kết quả các phép tính:

   a) 8,7 + 17,5;

   b) 24,45 – 16,67;

   c) (‒5,11) . (‒6,89);

   d) 5,39 . (4,21 +  9,89).

   Hướng dẫn giải

   a) 8,7 + 17,5 ≈ 9 + 18 = 27;

   b) 24,45 – 16,67 ≈ 24 – 17 = 7;

   c) (‒5,11) . (‒6,89) ≈ (‒5) . (‒7) = ‒ (5.7) = ‒35;

   d) 5,39 . (4,21 +  9,89) ≈ 5 . (4 + 10) = 5 . 14 = 70.

   Bài 22. Tính tỉ số của:

   a) 2 giờ và 6 giờ;

   b) 0,2 tạ và 12 kg;

   c)  m và 70 cm.

   Hướng dẫn giải

   a) Tỉ số của 2 giờ và 6 giờ là:

   2 : 6 = $\frac{2}{6}=\frac{1}{3}$.

   Vậy tỉ số của 2 giờ và 6 giờ là $\frac{1}{3}.$

   b) Đổi 0,2 tạ = 20 kg.

   Tỉ số của 20 kg và 12 kg là: $\frac{5}{3}.$

   20 : 12 = $\frac{20}{12}=\frac{5}{3}$.

   Vậy tỉ số của 0,2 tạ và 12 kg là  

   c) Đổi $\frac{3}{5}$ m = 0,6 m = 60 cm.

   Tỉ số của 60 cm và 70 cm là:

   60 : 70 =  $\frac{60}{70}=\frac{6}{7}.$

   Vậy tỉ số của $\frac{3}{5}$ m và 70 cm là $\frac{6}{7}.$

   Bài 23. Tính tỉ số phần trăm (làm tròn kết quả đến hàng phần trăm) của:

   a) 0,12 m² và 420 cm²;

   b) $\frac{2}{3}$ giờ và 12 phút.

   Hướng dẫn giải

   a) Đổi 0,12 m² = 12 cm²

   Tỉ số phần trăm của 12 cm² và 420 cm² là:  $\frac{12}{420}.100\%=\frac{12.100}{420}\%=2,\mathrm{857142\dots }\%$

   Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 5 = 5 nên ta có 2,857142…≈ 2,9.

   Vậy tỉ số phần trăm của 0,12 m² và 420 cm² là khoảng 2,9%.

   b) Đổi $\frac{2}{3}$ giờ = 40 phút.

   Tỉ số phần trăm 40 phút và 12 phút là: $\frac{40}{12}.100\%=\frac{40.100}{12}\%=333,\mathrm{3333..}\%$

   Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 3 < 5 nên ta có 333,33333…≈ 333,3.

   Vậy tỉ số phần trăm của $\frac{2}{3}$ giờ và 12 phút là 333,3%.

   Bài 24. Minh điều tra về loại quả ưa thích của một số bạn học sinh trong lớp, mỗi bạn trả lời một lần, được kết quả như bảng thống kê sau:

   Quả yêu thích	Cam	Ổi	Chuối	Khế	Xoài
   Số bạn chọn	6	4	3	5	7

   a) Có bao nhiêu bạn tham gia trả lời?

   b) Minh đưa ra kết luận rằng tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50%. Minh kết luận đúng hay không?

   Hướng dẫn giải

   a) Tổng số bạn tham gia trả lời là: 6 + 4 + 3 + 5 + 7 = 25 (bạn)

   Vậy có 25 bạn tham gia trả lời.

   b) Số bạn thích quả cam và xoài là: 6 + 7 = 13 (bạn)

   Tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn tham gia trả lời là:

   $\frac{13}{25}.100\%=\frac{13.100}{25}\%=52\%$.

   Do đó tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50%.

   Vậy Minh đã kết luận đúng.

   Bài 25. Tính:

   a) $\frac{4}{5}$ của ‒60;

   b) 75% của 16;

   c) $\frac{1}{5}$ của 225 000 đồng;

   d) Có bao nhiêu phút trong $\frac{5}{12}$ giờ?

   Hướng dẫn giải

   a) $\frac{4}{5}$ của ‒60 là: $\left(-60\right).\frac{4}{5}=-48$;

   b) 75% của 16 là: $16.\frac{75}{100}=12$;

   c) $\frac{1}{5}$ của 225 000 đồng là: 225 000 .$\frac{1}{5}=45000$(đồng);

   d) Ta có: $\frac{5}{12}$ giờ = 60 phút

   Số phút có trong  giờ là: 60. $\frac{5}{12}$ = 25 phút.

   Bài 26. Tìm một số, biết:

   a) $\frac{3}{25}$ của nó bằng 120;

   b) 0,015 của nó bằng ‒30;

   c) 120% của nó bằng 9 lít;

   d) 6% của nó bằng 102 cây.

   Hướng dẫn giải

   a) $\frac{3}{25}$ của một số bằng 120 nên số đó là: 120 : $\frac{3}{25}=120.\frac{25}{3}=1000$;

   b) 0,015 của nó bằng ‒30 nên số đó là: (‒30) : 0,015 = ‒2 000;

   c) 120% của nó bằng 9 lít nên số đó là: 8 : $\frac{120}{100}=9.\frac{100}{120}=7,5$(lít)

   d) 6% của nó bằng 102 cây nên số đó là: 102 : $\frac{6}{100}=102.\frac{100}{6}=1700$ (cây)

   Bài 27. Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường và muối theo thứ tự bằng 5%, $\frac{1}{1000}$ và $\frac{3}{40}$ khối lượng của rau cải. Vậy nếu muối 3 kg rau cải cần bao nhiêu ki – lô – gam hành, đường và muối?

   Hướng dẫn giải

   Số ki – lô – gam hành cần là: 3.5% = $3.\frac{5}{100}=0,15$ (kg)

   Số ki – lô – gam đường cần là:$3.\frac{1}{1000}=0,003$ (kg)

   Số ki – lô – gam muối cần là: $3.\frac{3}{40}=0,225$ (kg)

   Vậy để muối 3 kg rau cải cần 0,15 kg hành; 0,003 kg đường và 0,225 kg muối.

   Bài 28. Bố Lan gửi tiết kiệm 100 triệu đồng tại một ngân hàng theo kì hạn 12 tháng với lãi suất là 0,51% một tháng (tiền lãi mỗi tháng bằng 0,51% số tiền gửi ban đầu và sau 12 tháng mới được lấy lãi).

   a) Hỏi hết thời hạn 12 tháng, bố Lan lấy cả gốc lẫn lãi được bao nhiêu?

   b) Giả sử hết kì hạn 12 tháng, bố Lan không rút gốc và lãi thì sau 1 năm nữa, bố Lan rút cả gốc lẫn lãi là bao nhiêu? Biết rằng lãi suất không thay đổi.

   Hướng dẫn giải

   Ta có $0,51\%=\frac{0,51}{100}=\frac{51}{10000}$ 

   a) Số tiền lãi nhận được sau một tháng là:

   $100000000.\frac{51}{10000}=510000$ (đồng)

   Số tiền lãi nhận được sau 12 tháng là: 510 000 . 12 = 6 120 000 (đồng)

   Số tiền cả gốc lẫn lãi bố Lan lấy được sau 1 năm là:

   100 000 000 + 6 120 000 = 106 120 000 (đồng)

   b) Số tiền lãi nhận được sau một tháng (của năm thứ hai) là:

   106 120 000 . $\frac{51}{10000}=541212$ (đồng)

   Số tiền lãi nhận được sau 12 tháng là: 541 212 . 12 = 6 494 544 (đồng)

   Số tiền cả gốc lẫn lãi bố Lan lấy được sau 2 năm là:

   106 120 000 + 6 494 544 = 112 614 544 (đồng)

   Vậy số tiền bố Lan nhận được khi lấy cả gốc lẫn lãi sau 2 năm là 112 614 544 đồng.

   Bài 29. Một cửa hàng bán chiếc xe đạp với giá khuyến mãi giảm 15% so với giá niêm yết. Biết tin khuyến mãi nên mẹ đưa Bình ra cửa hàng mua cho chiếc xe đạp với giá 7 225 000 đồng. Hỏi chiếc xe đạp có giá niêm yết là bao nhiêu?

   Hướng dẫn giải

   Vì chiếc xe đạp được giảm 15% so với giá niêm yết nên mẹ Bình đã mua chiếc xe đó bằng 85% giá niêm yết.

   Giá niêm yết của chiếc xe là:

   7 225 000 : 85% = $7225000:\frac{85}{100}=7225000.\frac{100}{85}=8500000$ (đồng)

   Vậy chiếc xe có giá niêm yết là 8 500 000 đồng.

   Bài 30. Chỉ số khối của cơ thể (Body Mass Index) viết tắt là BMI thường được sử dụng để xác định tình trạng cơ thể ở mức bình thường, suy dinh dưỡng hay béo phì. Chỉ số này tính dựa trên chiều cao và cân nặng cơ thể, giúp chúng ta có cái nhìn khách quan nhất về tình trạng cân nặng bản thân. Chỉ số BMI được tính theo công thức $BMI=\frac{m}{h^2}$ (trong đó m là khối lượng cơ thể tính theo kg, h là chiều cao cơ thể tính theo mét). Thể trạng của học sinh lớp 6 theo chỉ số BMI như sau:

    BMI < 15: Gầy;

   18 ≤ BMI < 23: Bình thường;

   23 ≤ BMI < 30:  Béo phì nhẹ;

   30 ≤ BMI < 40: Béo phì trung bình;

   40 ≤ BMI: Béo phì nặng.

   Một bạn học sinh lớp 6 cao 150 cm, nặng 45 kg, theo em tình trạng cơ thể bạn ở mức nào?

   Hướng dẫn giải

   Đổi 150 cm = 1,5 m

   Chỉ số khối của cơ thể bạn học sinh đó là: $BMI=\frac{45}{1,5^2}=\frac{45}{1,5.1,5}=\frac{45}{2,25}=20$ 

   Vì 18 ≤ BMI < 23 nên bạn học sinh đó bình thường không bị béo phì cũng không bị gầy.

   Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:

   Lý thuyết Chương 2: Số nguyên

   Lý thuyết Chương 3: Hình học trực quan

   Lý thuyết Chương 4: Một số yếu tố thống kê và xác suất

   Lý thuyết Chương 5: Phân số và số thập phân

   Lý thuyết Chương 6: Hình học phẳng
3. Sách bài tập Toán 7 (Kết nối tri thức) Ôn tập chương 5
   Giải SBT Toán lớp 7 Ôn tập chương 5

   Giải trang 92 Tập 1

   A. Câu hỏi (trắc nghiệm)

   Tìm câu trả lời đúng trong các đáp án đã cho.

   Câu 1 trang 92 Tập 1: An hỏi các bạn trong lớp em bạn nào thuận tay trái, bạn nào thuận tay phải. Như vậy An đã thu thập dữ liệu bằng phương pháp:

   A. Quan sát.

   B. Làm thí nghiệm.

   C. Lập bảng hỏi.

   D. Phỏng vấn.

   Lời giải:

   Đáp án đúng là: D

   An hỏi các bạn trong lớp, như thế có nghĩa là An đã thu thập dữ liệu bằng phương pháp phỏng vấn.

   Câu 2 trang 92 Tập 1: Muốn so sánh các phần trong toàn bộ dữ liệu ta nên dùng:

   A. Biểu đồ tranh.

   B. Biểu đồ cột.

   C. Biểu đồ hình quạt tròn.

   D. Biểu đồ đoạn thẳng.

   Lời giải:

   Đáp án đúng là: C

   Biểu đồ hình quạt tròn dùng để so sánh các phần trong toàn bộ dữ liệu.

   Câu 3 trang 92 Tập 1: Trong biểu đồ hình quạt tròn, nửa hình tròn biểu diễn

   A. 25%.

   B. 50%.

   C. 75%.

   D. 100%.

   Lời giải:

   Đáp án đúng là: B

   Trong biểu đồ hình quạt tròn, cả hình tròn biểu diễn 100%, do đó nửa hình tròn biểu diễn 50%.

   Câu 4 trang 92 Tập 1: Trong biểu đồ hình quạt tròn, khẳng định nào sau đây không đúng?

   A. Hai hình quạt bằng nhau biểu diễn cùng một tỉ lệ.

   B. Hình quạt nào lớn hơn biểu diễn số liệu lớn hơn.

   C. Cả hình tròn biểu diễn 75%.

   D. $\frac{1}{4}$ hình tròn biểu diễn 25%.

   Lời giải:

   Đáp án đúng là: C

   Trong biểu đồ hình quạt tròn, cả hình tròn biểu diễn 100%, do đó câu C không đúng.

   Câu 5 trang 92 Tập 1: Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng

   A. Biểu đồ hình quạt tròn.

   B. Biểu đồ cột kép.

   C. Biểu đồ đoạn thẳng.

   D. Biểu đồ tranh.

   Lời giải:

   Đáp án đúng là: C

   Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng biểu đồ đoạn thẳng.

   Câu 6 trang 92 Tập 1: Trong biểu đồ đoạn thẳng, khẳng định nào sau đây không đúng?

   A. Gốc của trục đứng không nhất thiết phải là 0.

   B. Trục ngang biểu diễn thời gian.

   C. Giá trị của đại lượng tại một thời điểm có thể biểu diễn bằng dấu chấm tròn, dấu chấm vuông, dấu nhân,…

   D. Thời gian trên trục ngang không nhất thiết phải sắp xếp theo thứ tự tăng dần.

   Lời giải:

   Đáp án đúng là: D

   Biểu đồ đoạn thẳng thường được dùng để biểu diễn sự thay đổi của một đại lượng theo thời gian. Các thành phần của biểu đồ đoạn thẳng gồm:

   – Trục ngang biểu diễn thời gian và được sắp xếp theo thứ tự tăng dần;

   – Giá trị của đại lượng tại một thời điểm có thể biểu diễn bằng dấu chấm tròn, dấu chấm vuông, dấu nhân,…

   – Gốc của trục đứng không nhất thiết phải là 0 (chẳng hạn Biểu đồ D phần Thử thách nhỏ SGK Toán lớp 7 Tập 1 trang 104).

   Vậy đáp án D không đúng.

   Giải trang 93 Tập 1

   B. Bài tập

   Bài 5.25 trang 93 Tập 1: An đã hỏi một số bạn trong trường về hoạt động chiếm nhiều thời gian nhất trong tuần đầu tháng 6 vừa qua và thu được dữ liệu sau (D: Đi du lịch, C: Chơi thể thao, H: Học thêm, L: Làm việc nhà).

   HDHDDCDDHDCDCCDHDHDCDDCLDCLDLDLDDLCCDDCD

   a) An đã dùng phương pháp thu thập dữ liệu nào: quan sát, làm thí nghiệm, lập bảng hỏi hay phỏng vấn?

   b) Dữ liệu thu được thuộc loại nào?

   c) Hoàn thiện bảng thống kê sau vào vở.

   Hoạt động	Đi du lịch	Chơi thể thao	Học thêm	Làm việc nhà
   Số bạn	20	?	?	?

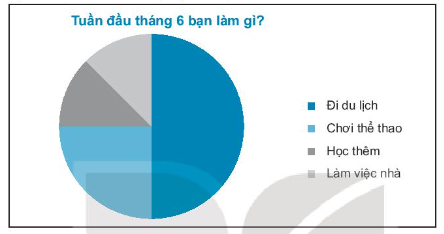
   d) Hoàn thiện biểu đồ hình quạt tròn Hình 5.18 vào vở.

   

   Lời giải:

   a) An đã dùng phương pháp phỏng vấn để thu thập dữ liệu (vì An đã hỏi một số bạn trong trường).

   b) Dữ liệu thu được là dữ liệu không là số, không thể sắp thứ tự.

   c) Trong dãy dữ liệu đã thu được ở trên có 10 chữ cái C, tức là có 10 bạn dành nhiều thời gian chơi thể thao; có 5 chữ cái H nên có 5 bạn dành nhiều thời gian học thêm; có 5 chữ cái L, có nghĩa là có 5 bạn dành nhiều thời gian làm việc nhà và có 20 chữ cái D, điều đó có nghĩa là có 20 bạn dành nhiều thời gian đi du lịch.

   Ta có bảng thống kê sau:

   Hoạt động	Đi du lịch	Chơi thể thao	Học thêm	Làm việc nhà
   Số bạn	20	10	5	5

    d) Từ bảng thống kê ta thấy có tổng 40 bạn được hỏi, trong đó có:

   + 20 bạn đi du lịch, chiếm $\frac{20}{40}.100\%=50\%$ tổng số bạn, tương ứng với phần hình quạt lớn nhất trong Hình 5.18.

   + 10 bạn chơi thể thao, chiếm $\frac{10}{40}.100\%=25\%$ tổng số bạn, tương ứng với phần hình quạt bằng $\frac{1}{4}$ hình tròn.

   + Số bạn học thêm và làm việc nhà là bằng nhau nên tương ứng với hai phần hình quạt bằng nhau trong Hình 5.18.

   Vậy ta hoàn thiện được biểu đồ như sau:

   

   Bài 5.26 trang 93 Tập 1: Minh làm bài kiểm tra trình độ tiếng Anh trên mạng Internet 6 lần và ghi lại kết quả (tỉ lệ số câu đúng) như sau:

   Lần	1	2	3	4	5	6
   Kết quả (%)	20	60	80	90	95	97

    a) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

   b) Nhận xét về sự tiến bộ của Minh sau mỗi lần làm bài.

   Lời giải:

   a) Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu về kết quả làm bài kiểm tra trình độ tiếng Anh trên mạng Internet của bạn Minh trong bảng trên, ta thực hiện theo các bước sau:

   Bước 1. Vẽ trục ngang biểu diễn thứ tự các lần, trục đứng biểu diễn kết quả (%).

   Bước 2. Với mỗi số thứ tự trên trục ngang, kết quả làm bài kiểm tra của lần đó được biểu diễn bởi một điểm.

   Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

   Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm và đặt tên cho biểu đồ để hoàn thiện biểu đồ.

   

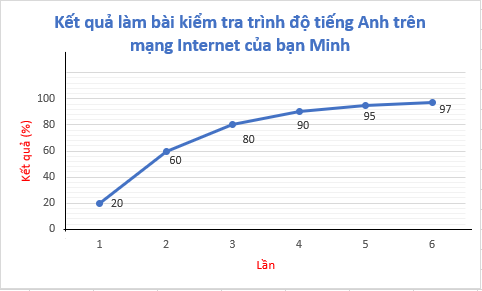
   b) Điểm số của bạn Minh có xu thế tăng dần theo số lần làm bài, điểm số tăng với tốc độ nhanh, từ lần đầu làm chỉ được 20%, lần thứ 6 làm bài đã đạt được 97%. Tốc độ tăng ở những lần đầu nhanh hơn so với tốc độ tăng ở những lần cuối.

   Giải trang 94 Tập 1

   Bài 5.27 trang 94 Tập 1: Nhà trường vận động mỗi bạn tặng một món quà cho các bạn học sinh vùng lũ lụt. Biểu đồ Hình 5.19 biểu diễn tỉ lệ học sinh lớp 7A tặng các món quà khác nhau.

   

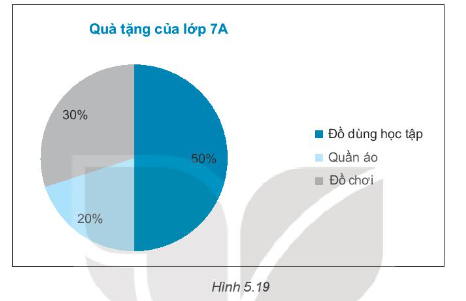
   Lớp 7A có 40 học sinh. Tính số học sinh tặng từng loại món quà.

   Lời giải:

   Quan sát biểu đồ Hình 5.19, ta thấy số học sinh tặng đồ dùng học tập chiếm 50% số học sinh cả lớp 7A, do đó có 40 . 50% = 40 . 50 : 100 = 20 học sinh tặng đồ dùng học tập.

   Số học sinh tặng quần áo chiếm 20% số học sinh cả lớp 7A, do đó có 40 . 20% = 40 . 20 : 100 = 8 học sinh tặng quần áo.

   Số học sinh tặng đồ chơi là: 40 – 20 – 8 = 12 (bạn).

   Vậy có 20 bạn tặng quà là đồ dùng học tập, 8 bạn tặng quà là quần áo và 12 bạn tặng quà là đồ chơi.

   Bài 5.28 trang 94 Tập 1: Đóng góp trực tiếp (đơn vị tỉ đô la) của ngành du lịch cho GDP toàn cầu từ năm 2015 đến năm 2019 được cho trong bảng thống kê sau:

   Năm	2015	2016	2017	2018	2019
   Lượng đóng góp	2,3	2,4	2,4	2,6	2,9

    a) Lượng đóng góp trực tiếp của ngành du lịch cho GDP toàn cầu thuộc loại dữ liệu nào?

   b) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

   c) Cho biết xu thế về đóng góp trực tiếp của du lịch cho GDP toàn cầu trong thời gian này.

   Lời giải:

   a) Lượng đóng góp trực tiếp của ngành du lịch cho GDP toàn cầu thuộc loại dữ liệu là số liệu.

   b) Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu về lượng đóng góp trực tiếp của ngành du lịch cho GDP toàn cầu trong bảng trên, ta thực hiện theo các bước sau:

   Bước 1. Vẽ trục ngang biểu diễn các năm, trục đứng biểu diễn lượng đóng góp cho GDP toàn cầu (tỉ đô la).

   Bước 2. Với mỗi số thứ tự trên trục ngang, lượng đóng góp của năm đó được biểu diễn bởi một điểm.

   Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

   Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm và đặt tên cho biểu đồ để hoàn thiện biểu đồ.

   

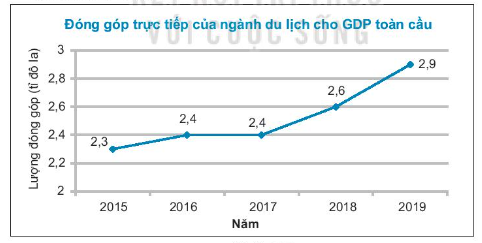
   c) Từ biểu đồ trên, ta thấy lượng đóng góp trực tiếp của ngành du lịch cho GDP toàn cầu có xu thế tăng theo thời gian trong các năm từ 2015 đến 2019.

   Bài 5.29 trang 94 Tập 1: Tỉ lệ nghèo đói tính trên tổng số dân của Mỹ trong các năm từ 2015 đến 2019 được cho trong biểu đồ Hình 5.20.

   

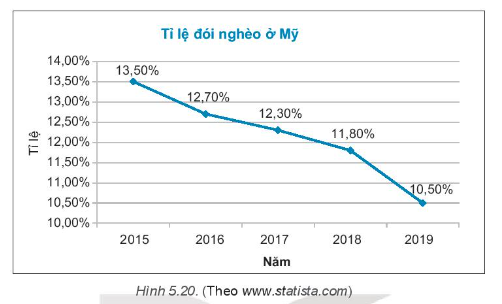
   a) Cho biết xu thế của tỉ lệ đói nghèo tại Mỹ trong thời gian trên.

   b) Lập bảng thống kê biểu diễn số liệu biểu diễn trong biểu đồ.

   c) Năm 2019 dân số Mỹ là 328 triệu người (theo World Bank), tính số người đói nghèo ở Mỹ.

   Lời giải:

   a) Từ biểu đồ Hình 5.20, ta thấy tỉ lệ đói nghèo tại Mỹ có xu thế giảm dần theo thời gian trong các năm từ 2015 đến 2019.

   b) Quan sát biểu đồ Hình 5.20, ta có tỉ lệ đói nghèo các năm là:

   – Năm 2015: 13,50%;

   – Năm 2016: 12,70%;

   – Năm 2017: 12,30%;

   – Năm 2018: 11,80%;

   – Năm 2019: 10,50%;

   Vậy ta lập được bảng thống kê như sau:

   Năm	2015	2016	2017	2018	2019
   Tỉ lệ đói nghèo	13,50%	12,70%	12,30%	11,80%	10,50%

    c) Năm 2019, tỉ lệ đói nghèo ở Mỹ chiếm 10,50% tổng số dân, do đó, số người đói nghèo ở Mỹ trong năm này là:

   328 . 10,50% = 328 . 10,50 : 100 = 34,44 triệu người = 34 440 000 người.

   Vậy năm 2019, Mỹ có 34 440 000 người đói nghèo.

   Giải trang 95 Tập 1

   Bài 5.30 trang 95 Tập 1: Cho biểu đồ Hình 5.21.

   

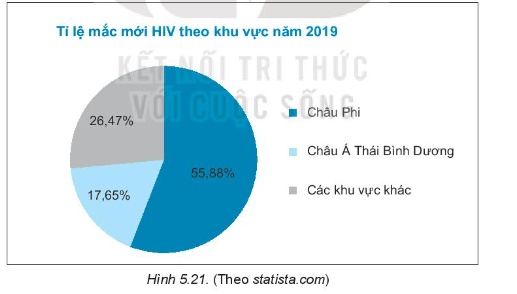
   a) Lập bảng thống kê biểu diễn tỉ lệ mắc mới HIV theo vùng năm 2019.

   b) Năm 2019, thế giới có 1 700 ca mắc mới HIV. Số lượng mắc mới HIV của mỗi khu vực trên khoảng bao nhiêu người?

   Lời giải:

   a) Từ biểu đồ Hình 5.21, ta thấy tỉ lệ mắc mới HIV năm 2019 ở Châu Phi chiếm 55,88%, ở Châu Á Thái Bình Dương chiếm 17,65% và ở các khu vực khác chiếm 26,47%.

   Vậy ta có bảng thống kê sau:

   Khu vực	Châu Phi	Châu Á Thái Bình Dương	Các khu vực khác
   Tỉ lệ mắc mới HIV	55,88%	17,65%	26,47%

    b) Số lượng người mắc mới HIV ở Châu Phi là: 1 700 . 55,88% ≈ 950 (người).

   Số lượng người mắc mới HIV ở Châu Á Thái Bình Dương là: 1 700 . 17,65% ≈ 300 (người).

   Số lượng người mắc mới HIV ở các khu vực khác là: 1 700 – 950 – 300 = 450 (người).

   Vậy số lượng người mắc mới HIV ở Châu Phi, Châu Á Thái Bình Dương và các khu vực khác lần lượt khoảng 950, 300 và 450 người.

   Giải trang 96 Tập 1

   Bài 5.31 trang 96 Tập 1: Một nghiên cứu đã đưa ra tỉ lệ học sinh cấp THCS nghiện điện thoại di động trong những năm gần đây như biểu đồ Hình 5.22.

   

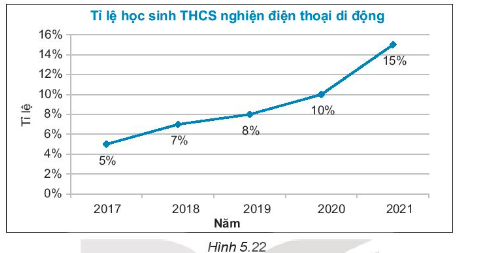
   a) Trục đứng biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?

   b) Năm 2021, một trường THCS có 1 000 học sinh. Hãy ước lượng số lượng học sinh nghiện điện thoại di động của trường.

   Lời giải:

   a) Từ biểu đồ Hình 5.22, ta thấy trục đứng biểu diễn tỉ lệ học sinh THCS nghiện điện thoại di động, dữ liệu về đại lượng này thuộc loại dữ liệu là số liệu.

   b) Từ biểu đồ Hình 5.22, ta thấy năm 2021, tỉ lệ học sinh THCS nghiện điện thoại di động chiếm 15% tổng số học sinh.

   Do đó số học sinh nghiện điện thoại di động trong 1 000 học sinh của một trường THCS năm 2021 là: 1 000 . 15% = 1 000 . 15 : 100 = 150 (học sinh).

   Bài 5.32 trang 96 Tập 1: Cho biểu đồ Hình 5.23.

   

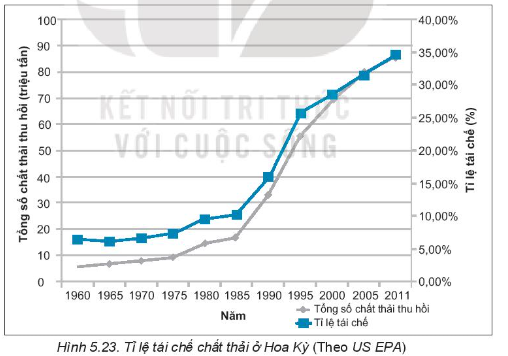
   a) Các đường màu xanh, màu xám biểu diễn những dãy số liệu nào?

   b) Mỗi trục đứng bên trái, bên phải biểu diễn giá trị ứng với đường nào?

   Lời giải:

   Quan sát biểu đồ Hình 5.23, ta có:

   a) Đường màu xanh biểu diễn dãy số liệu về tỉ lệ tái chế chất thải ở Hoa Kỳ trong các năm từ 1960 đến 2011.

   Đường màu xám biểu diễn dãy số liệu về tổng số chất thải thu hồi ở Hoa Kỳ trong các năm từ 1960 đến 2011.

   b) Trục đứng bên trái biểu diễn tổng số chất thải thu hồi ở Hoa Kỳ, đơn vị triệu tấn.

   Trục đứng bên phải biểu diễn tỉ lệ tái chế chất thải ở Hoa Kỳ, đơn vị phần trăm (%).

   Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

   Bài 19: Biểu đồ đoạn thẳng

   Ôn tập chương 5

   Bài 20: Tỉ lệ thức

   Bài 21: Tính chất của dãy tỉ số bằng nhau

   Bài 22: Đại lượng tỉ lệ thuận
4. Giải SGK Sinh học 10 (Chân trời sáng tạo) Ôn tập chương 5
   Giải bài tập Sinh học lớp 10 Ôn tập chương 5

   Bài tập

   Giải Sinh học 10 trang 139

   Bài 1 trang 139 Sinh học 10: Hình thức dinh dưỡng của vi sinh vật rất đa dạng, điều này có ý nghĩa gì đối với tự nhiên?

   Hướng dẫn giải:

   Dựa vào nguồn năng lượng và carbon sử dụng, vi sinh vật được chia thành 4 kiểu dinh dưỡng khác nhau: quang tự dưỡng, quang dị dưỡng, hoá tự dưỡng và hoá dị dưỡng.

   Trả lời:

   Các hình thức dinh dưỡng của vi sinh vật rất đa dạng thể hiện tự nhiên có nguồn vật chất và điều kiện môi trường rất đa dạng. Các hình thức dinh dưỡng của vi sinh vật còn giúp tự nhiên cân bằng các vật chất, giúp tự nhiên phân giải các chất dư thừa và tổng hợp nên các chất còn thiếu.

   Bài 2 trang 139 Sinh học 10: Hãy giải thích vì sao khi làm sữa chua, chúng ta cần sát trùng tất cả các dụng cụ bằng nước sôi.

   Hướng dẫn giải:

   Sữa chua là quá trình lên men đường từ sữa của các vi khuẩn lactic.

   Trả lời:

   Khi sát trùng tất cả dụng cụ sẽ tiêu diệt bớt các vi khuẩn ở các dụng cụ, giúp hoạt động lên men của vi khuẩn lactic được thuận lợi.

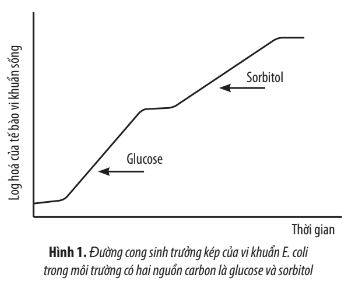
   Bài 3 trang 139 Sinh học 10: Quan sát đồ thị ở Hình 1, hãy giải thích sự sinh trưởng của quần thể vi khuẩn E. coli trong môi trường có hai nguồn carbon là glucose và sorbitol.

   

   Hướng dẫn giải:

   Quan sát hình, dựa vào các kiến thức về sinh trưởng của vi sinh vật để giải thích.

   Trả lời:

   – Ở giai đoạn đầu, vi khuẩn E.coli đang thích nghi với môi trường mới, số lượng tế bào chết bằng số lượng tế bào sinh ra nên đường cong sinh trưởng là đường không thay đổi.

   – Khi đã thích nghi với môi trường, vi sinh vật sử dụng glucose làm dinh dưỡng nên các tế bào sinh trường mạnh mẽ, lượng tế bào sinh ra lớn hơn so với số tế bào chết đi, đường cong sinh trường lúc này tăng lên và đạt mức tối đa.

   – Giai đoạn tiếp theo, đường cong sinh trường không thay đổi vì dinh dưỡng bắt đầu giảm dẫn, số lượng tế bào chết bằng số lượng tế bào sinh ra.

   – Ở giai đoạn tiếp theo, khi cho thêm sorbitol, vi khuẩn E.coli tăng số lượng tế bào do được cung cấp thêm dinh dưỡng cho sự sinh trường, số tế bào được sinh ra nhiều hơn số tế bào chết đi nên đường cong sinh trường tăng đến cực đại.

   – Ở giai đoạn cuối, khi dinh dưỡng tiếp tục dần cạn kiệt, số tế bào chết bằng số tế bào sinh ra, đường cong sinh trường không thay đổi.

   Bài 4 trang 139 Sinh học 10: Người dân đã dựa vào cơ sở khoa học nào để làm nước mắm từ cá? Độ đạm của nước mắm là gì?

   Hướng dẫn giải:

   Nước mắm là sản phẩm của quá trình phân giải protein có trong cá thành các acid amin. Hàm lượng nitơ trong các acid amin của nước mắm để xác định độ đạm của nước mắm

   Trả lời:
   – Người dân đã dựa vào khả năng phân giải protein của vi sinh vật để làm nước mắm từ cá.

   – Độ đạm là tổng hàm lượng nitơ có trong 1 lít nước mắm.

   Bài 5 trang 139 Sinh học 10: Hãy hoàn thành nội dung của bảng sau:

   

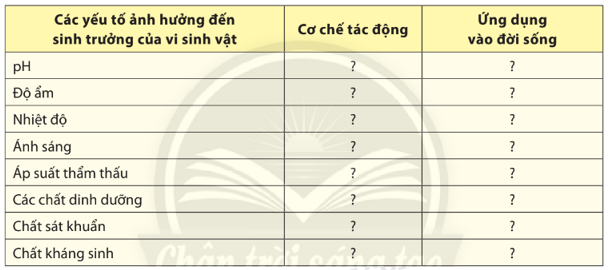
   Hướng dẫn giải:

   Các yếu tố ảnh hưởng đến sinh trưởng của vi sinh vật gồm:

   – Các yếu tố hóa học:

   + Chất dinh dưỡng: Những chất này ảnh hưởng đến quá trình chuyển hoá vật chất và năng lượng của vi sinh vật (quá trình dinh dưỡng, hô hấp, hoạt hóa enzyme, cân bằng thẩm thấu,..).

   + Chất sát khuẩn: là các chất có khả năng tiêu diệt hoặc ức chế không chọn lọc các vi sinh vật gây bệnh nhưng không làm tổn thương đến da và mô sống của cơ thể (phenol, ethanol, các halogens,…).

   + Chất kháng sinh: là những hợp chất hữu cơ có khả năng tiêu diệt hoặc ức chế vi sinh vật gây bệnh theo nhiều cơ chế khác nhau, như ức chế tổng hợp thành tế bào, protein, nucleic acid,…

   – Các yếu tố vật lý:

   + pH: Độ pH ảnh hưởng đến tính thẩm qua màng, hoạt động chuyển hoá vật chất trong tế bào, hoạt tính enzyme,… Giới hạn hoạt động của đa số vi khuẩn nằm trong khoảng pH từ 4 đến 10. Một số vi khuẩn chịu acid có thể sinh trưởng ở pH ≥ 1.

   + Nhiệt độ: Nhiệt độ ảnh hưởng đến tốc độ phản ứng sinh hoá trong tế bào; mỗi loại vi sinh vật có thể tồn tại và hoạt động tốt nhất trong một phạm vi nhiệt độ nhất định.

   + Độ ẩm: Vi sinh vật rất cần nước, vì nước là dung môi hoà tan các chất dinh dưỡng, enzyme, thuỷ phân cơ chất. Nếu không có nước, vi sinh vật sẽ ngừng sinh trưởng và hầu hết sẽ chết. Các loại vi sinh vật đòi hỏi độ ẩm khác nhau: vi khuẩn (độ ẩm cao); nấm mốc, nấm men (độ ẩm thấp).

   + Áp suất thẩm thấu: Khi đưa vi sinh vật vào môi trường ưu trương (môi trường có nồng độ chất tan cao hơn bên trong tế bào), tế bào vi sinh vật sẽ bị mất nước, gây co nguyên sinh, do đó chúng không phân chia được.

   + Ánh sáng: Ánh sáng tác động đến quá trình quang hợp ở vi khuẩn quang tự dưỡng, ngoài ra ánh sáng còn ảnh hưởng đến sự hình thành bào tử, tổng hợp sắc tố, chuyển động hướng sáng,… Những tia sáng có bước sóng ngắn có thể ức chế hoặc tiêu diệt vi khuẩn bằng cách gây đột biến, làm biến tính protein,…

   Trả lời:

   

   Bài 6 trang 139 Sinh học 10: Liệt kê một số thành tựu và tên các ngành nghề liên quan đến ứng dụng công nghệ vi sinh vật trong đời sống theo nội dung bảng sau:

   

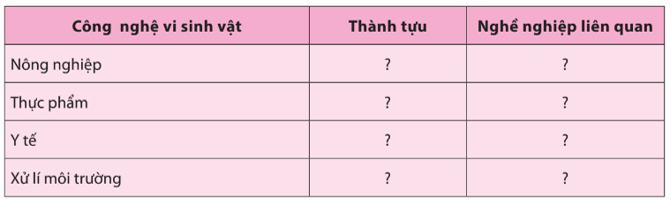
   Hướng dẫn giải:

   – Các thành tựu của công nghệ sinh học:

   + Trong nông nghiệp: tạo các chế phẩm sinh học làm phân bón vi sinh hoặc thuốc trừ sâu sinh học.

   + Trong công nghiệp thực phẩm: Sản xuất các loại nước uống, bánh mì, phomai, các sản phẩm cung cấp vi khuẩn có lợi như sữa chua,…

   + Trong y học: Tạo các loại vaccine, kháng thể, hormone,…

   + Trong xử lý ô nhiễm môi trường; Tạo các chế phẩm xử lý rác thải hữu cơ trong môi trường, đồng thời tạo ra các sản phẩm phụ có lợi cho con người như phân bón hữu cơ, khí sinh học,…

   – Một số ngành nghề liên quan đến công nghệ sinh học là: kỹ sư (thiết kế phần mềm, thiết kế và vận hành máy móc, quản lý các dự án có liên quan đến ứng dụng vi sinh vật), kỹ thuật viên (làm việc tại các cơ sở y tế, nhà máy sản xuất,…), chuyên viên tư vấn các vấn đề liên quan đến vi sinh vật, nhà dịch tễ học,…

   Trả lời:

   

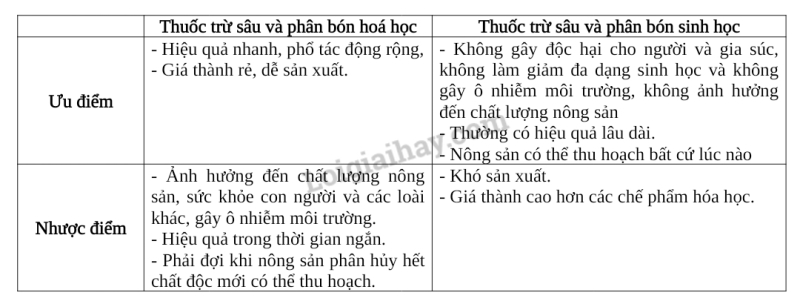
   Bài 7 trang 139 Sinh học 10: Hãy so sánh ưu điểm, nhược điểm của thuốc trừ sâu và phân bón hoá học với thuốc trừ sâu và phân bón sinh học.

   Hướng dẫn giải:

   – Thuốc trừ sâu và phân bón hóa học là sản phẩm chứa các loại hóa chất gây độc cho các loại gây hại cho cây trồng. Thuốc trừ sâu và phân bón hóa học có hiệu quả nhanh, phổ tác động rộng nhưng ảnh hưởng xấu đến sức khỏe con người khi hít phải hoặc ăn phải cây trồng chưa phân hủy hết chất độc, gây ô nhiễm môi trường, làm giảm đa dạng sinh học,…

   – Thuốc trừ sâu và phân bón sinh học là sản phẩm ứng dụng công nghệ vi sinh có chọn lọc. Thuốc trừ sâu và phân bón hóa học tuy hiệu lực chậm, phổ tác động hẹp, nhưng không gây độc cho con người và không gây ô nhiễm môi trường

   Trả lời:

   

   Xem thêm các bài giải SGK Sinh học lớp 10 Chân trời sáng tạo hay, chi tiết khác:

   Bài 28: Thực hành: Lên men

   Bài 29: Virus

   Bài 30: Ứng dụng của virus trong y học và thực tiễn

   Bài 31: Virus gây bệnh
5. Giải SGK Công nghệ 10 (Kết nối tri thức) Ôn tập chương 5
   Giải bài tập Công nghệ lớp 10 Ôn tập chương 5

   Câu hỏi 1 trang 95 Công nghệ 10: Phân biệt sâu hại và bệnh hại cây trồng. Kể tên một số loại sâu, bệnh hại cây trồng mà em biết.

   Trả lời:

   Sâu hại là các loài côn trùng gây hại các bộ phận của cây trồng như thân, lá, hoa, quả, rễ… Chúng làm lá bị khuyết, thủng, cuốn; quả, thân, cành bị gãy, thối, rụng…

   Một số sâu hại thường gặp là châu chấu, sâu cuốn lá, rệp, bọ hung, ruồi đục quả, sâu xanh…

   Bệnh hại là trạng thái không bình thường về hình thái, cấu tạo, chức năng, sinh lí… của cây trồng, do các loài sinh vật (nấm, vi khuẩn, virus…) hoặc điều kiện bất lợi gây ra. 

   Một số bệnh hại thường gặp như bệnh bạc à, bệnh đạo ôn trên lúa, bệnh thán thư, bệnh vàng lá greening trên cây có múi, bệnh héo xanh vi khuẩn, bệnh virus xoăn vàng lá đậu đũa,…

   Câu hỏi 2 trang 95 Công nghệ 10: Trình bày tác hại của sâu, bệnh đối với cây trồng.

   Trả lời:

   – Sâu, bệnh hại có ảnh hưởng xấu đến cây trồng:

   – Cây sinh trưởng, phát triển kém

   – Năng suất và chất lượng nông sản giảm, thậm chí không cho thu hoạch hoặc cây trồng bị chết.

   Câu hỏi 3 trang 95 Công nghệ 10: Các biện pháp phòng trừ sâu, bệnh hại cây trồng và ý nghĩa của việc phòng trừ.

   Trả lời:

   	Khái niệm	Ưu điểm	Nhược điểm
   1. Biện pháp canh tác	Là việc áp dụng các kĩ thuật trồng trọt như vệ sinh đồng ruộng, làm đất, bón phân, tưới nước, luân canh, xen canh cây trồng… nhằm mục đích loại bỏ mầm sâu, bệnh; hạn chế sự phát triển của sâu, bệnh hại, tạo điều kiện thuận lợi cho cây trồng sinh trưởng khỏe mạnh, tăng khả năng chống sâu bệnh.	Đơn giản, dễ thực hiện, dễ áp dụng rộng rãi và thân thiện với môi trường.	Mang tính ngăn ngừa là chính.
   2. Biện pháp cơ giới, vật lí	Là việc dùng sức người, dụng cụ, máy móc, bẫy để ngăn chặn, bắt, tiêu diệt, loại bỏ sâu, bệnh hại.	Dễ thực hiện, mang lại hiệu quả ngay và không gây ô nhiễm môi trường.	Tốn nhiều công lao động, tốn kém khi áp dụng trên diện rộng.
   3. Biện pháp sinh học	Là việc sử dụng sinh vật có ích hoặc sản phẩm của chúng để tiêu diệt sâu, bệnh hại cây trồng.	Có tác dụng lâu dài, an toàn với con người, cây trồng và thân thiện với môi trường.	Giá thành cao, tác động chậm, hiệu quả thấp khi sâu, bệnh hại đã bùng phát.
   4. Biện pháp hóa học	Là sử dụng các thuốc hóa học để phòng trừ sâu, bệnh hại.	Dễ sử dụng, hiệu quả nhanh, đặc biệt khi sâu, bệnh đã bùng phát.	Có thể gây ảnh hưởng đến sức khỏe con người, sản phẩm trồng trọt, làm ô nhiễm môi trường, giảm đa dạng sinh học, hình thành kháng thuốc ở sâu, bệnh hại.
   5. Biện pháp quản lí dịch hại tổng hợp (IPM)	Là sử dụng phối hợp đồng thời nhiều biện pháp phòng trừ sâu, bệnh hại cây trồng trong đó chú trọng biện pháp sinh học nhằm hạn chế số lượng các loài sâu, bệnh hại ở dưới ngưỡng gây thiệt hại kinh tế.	Giảm chi phí bảo vệ thực vật, tăng năng suất, chất lượng cây trồng và bảo vệ đa dạng sinh học.	Đòi hỏi người nông dân phải có kiến thức về hệ sinh thái cây trồng.

   Ý nghĩa của việc phòng trừ sâu, bệnh hại cây trồng:

   – Giúp bảo vệ cây trồng, hạn chế ảnh hưởng xấu của sâu, bệnh đối với cây trồng, tạo điều kiện cho cây trồng sinh trưởng và phát triển tốt, năng suất cao, chất lượng tốt.

   – Việc áp dụng các biện pháp sinh học và biện pháp quản lí dịch hại tổng hợp trong phòng trừ sâu, bệnh hại có tác dụng bảo vệ môi trường, bảo vệ hệ sinh thái và sức khỏe con người.

   Câu hỏi 4 trang 95 Công nghệ 10: So sánh đặc điểm của sâu tơ hại rau và sâu keo mùa thu.

   Trả lời:

   	Sâu tơ hại rau	Sâu keo mùa thu
   Đặc điểm hình thái, sinh học	– Có tên khoa học là Plutella xylostella, học Ngài rau, bộ Cánh vảy.     – Sâu trưởng thành có chiều dài nhỏ hơn 10mm. Cánh trước màu nâu, giữa lưng có một dải gợn sóng màu trắng (ngài đực) hoặc màu vàng (ngài cái). Râu và đầu dài, vươn về phía trước rất linh hoạt.     – Trứng hình bầu dục hơi tròn, màu vàng nhạt. Trứng đẻ rời rạc ở mặt dưới lá, gần gân chính.     – Sâu non hình ống, màu xanh nhạt, dài khoảng 10mm, đầu màu nâu vàng, trên mỗi đốt chân đều có lông tơ.   – Nhộng của sâu được bọc trong lớp kén tơ mỏng màu trắng nên được gọi là sâu tơ. Nhộng có màu xanh nhạt hoặc vàng nhạt, dài khaorng 6 – 8mm.	– Có tên khoa học là Spodoptera frugiperda, họ Ngài đêm, bộ Cánh vảy.     – Sâu keo mùa thu trưởng thành cánh trước có màu nâu xám, mép ngoài cánh trước có các đường vân, gợn hình sóng theo mép ngoài của cánh. Cánh sau màu vàng nhạt.     – Trứng hình cầu, màu trắng xanh đẻ thành ổ, có phủ lông tơ mỏng.     – Sâu non: đầu có vân hình chữ Y ngược, mặt lưng đốt cuối có 4 u lông màu đen xếp hình vuông.   – Nhộng màu nâu đỏ bóng, cuối bụng có đôi gai nhọn.
   Đặc điểm gây hại	Sâu non ăn biểu bì lá tạo thành những vết trong, mờ ở lá rau. Sâu tuổi lớn ăn thủng lá, làm giảm năng suất và chất lượng rau. Khi mật độ sâu cao, vườn rau bị hại xơ xác, chỉ còn trơ lại gân lá.	Gây hại chủ yếu trên ngô. Sâu non ăn lá tạo các lỗ thủng lớn trên phiến lá, cắn gẫy cờ, đục phá hại bắp ngô.
   Biện pháp phòng trừ	– Trồng xen rau thuộc học cải với các loại rau thuộc loại khác như hành, tỏi, cà chua hoặc luân canh với cây lúa nước.     – Sử dụng bẫy để bắt sâu tơ.   – Sử dụng thuốc bảo vệ thực vật và các chế phẩm sinh học…	– Vệ sinh đồng ruộng, cày lật đất để tiêu diệt nhộng, luân canh với cây lúa nước.     – Sử dụng bẫy để thu bắt sâu trưởng thành, ngắt bỏ ổ trứng.   – Sử dụng ong kí sinh hoặc phun chế phẩm sinh học để tiêu diệt sâu non, nhộng. Sử dụng thuốc trừ sâu theo đúng hướng dẫn.

   Câu hỏi 5 trang 95 Công nghệ 10: Trình bày đặc điểm nhận biết và biện pháp phòng trừ ruồi đục quả, rầy nâu hại lúa.

   Trả lời:

   	Ruồi đục quả	Rầy nâu hại lúa
   Đặc điểm nhận biết	– Ruồi đục quả trưởng thành dài gần 1cm, cơ thể màu vàng hoặc đen, bụng tròn; ngực có hai sọc vàng rộng, đốt bụng có chữ T màu đen. – Trứng có màu trắng trong hoặc vàng kem, hình trụ thon, dài và đầu hơi nhọn. – Sâu non (dòi) có màu trắng đục hơi vàng, không có chân, móc miệng có màu đen. Nhộng có màu nâu kem. – Trên quả bị ruồi đục phá có các vết chính màu đen, sau chuyển nâu. Phần thịt quả bị thối, quả rụng.	– Rầy trưởng thành có màu nâu, thân dài khoảng 3-5mm. Có hai dạng rầy trưởng thành: loại cánh dài và loại cánh ngắn. – Trứng được đẻ thành ổ giống hình nải chuối ở bẹ lá, có màu trắng đục. – Rầy nâu chích hút nhựa cây làm cho cây bị khô héo và chết. Khi mật độ rầy cao, lúa chết thành từng đám gọi là cháy rầy.
   Biện pháp phòng trừ	– Vệ sinh đông ruộng, sử dụng túi bọc quả, thu nhặt và tiêu hủy quả rụng. – Sử dụng bẫy để thu bắt ruồi trưởng thành. – Dùng thuốc trừ sâu theo đúng hướng dẫn.	– Sử dụng giống kháng bệnh là biện pháp quan trọng nhất để phòng trừ rầy nâu – Sử dụng biện pháp xử lí hạt giống, vệ sinh đồng ruộng, trồng đúng thời vụ, tránh mùa vụ gối nhau, bón phân đúng lúc và cân đối. – Sử dụng thuốc trừ sâu đúng quy định và sử dụng kẻ thù tự nhiên như thả vịt, thả cá rô phi, bọ xít mù xanh… và chế phẩm sinh học.

   Câu hỏi 6 trang 95 Công nghệ 10: Trình bày đặc điểm nhận biết và biện pháp phòng trừ bệnh thán thư, bệnh vàng lá greening, bệnh héo xanh vi khuẩn, bệnh đạo ôn trên lúa.

   Trả lời:

   		Đặc điểm nhận biết	Biện pháp phòng trừ
   Bệnh thán thư		– Trên lá: Bệnh thường gây hại từ mép lá, lúc đầu vết bệnh là các đốm nhỏ, sau liên kết thành mảng lớn, xung quanh có đường viền nâu sẫm. – Trên chồi non: Lúc đầu vết bệnh dạng thấm nước, sau chuyển màu nâu tối, chồi bị chết khô khi trời nắng hoặc thối khi trời mưa. – Trên hoa và quả: Vết bệnh hơi lõm xuống kiểu chấm đen, làm hoa và quả chuyển màu đen và rụng.	– Vệ sinh đồng ruộng, dọn sạch cành già, lá bệnh, bọc quả sau khi hình thành. – Trong màu mưa không để vườn quá ẩm thấp, có biện pháp thoát nước nhanh sau khi mưa lớn. – Chú ý bón phân đầy đủ và cân đối NPK. – Khi cây bị bệnh cần phun thuốc kịp thời và theo đúng hướng dẫn của nhà sản xuất.
   Bệnh vàng lá greening		Bệnh thường gây hại ở lá và quả. Lá bị bệnh thường lốn đốm vàng xanh, gân lá bị sung, có màu xanh, lá bị rụng. Quả nhỏ, bị méo, vàng loang lổ.	– Sử dụng nguồn ngây giống sạch bệnh. – Tạo tán, tỉa cành để vườn thông thoáng, tránh giao tán cây. – Bón phân hữu cơ đầy đủ, cân đối để giúp cây chống chịu tốt. – Quản lí tốt nguồn rầy chống cánh, đây là vật trung gian truyền bệnh. – Khi phát hiện cây bị bệnh cần cắt bỏ phần bị bệnh hoặc nhổ cây và đem hủy.
   Bệnh héo xanh vi khuẩn		– Khi bị bệnh, cành và lá héo rũ, ỏ thân phía gốc xù xì nhưng thân vẫn rắn đặc. Cắt ngang thân, cành thấy chứa dịch nhầy vi khuẩn. – Khi bị bệnh nặng, thân vỏ vẫn còn xanh, xuất hiện những sọc nâu.	– Sử dụng giống chống bệnh, giống khỏe và sạch bệnh. – Vệ sinh đồng ruộng, ngâm nước trong ruộng từ 15 đến  30 ngày hoặc cày đất, luân canh với cây lúa nước. – Sử dụng các chế phẩm sinh học phòng trừ bệnh.
   Bệnh đạo ôn hại lúa		– Vết bệnh trên lá lúa: chấm nhỏ màu xanh lục, mờ, sau đố có hình thoi, màu nâu nhạt, có quầng màu vàng nhạt, phần giữa vết bệnh có màu tro xám. – Vết bệnh ở cổ bông, cổ gié và trên hạt lúa: các vết màu nâu xám hơi teo thắt lại, dễ làm gãy cổ bông.	– Sử dụng giống chống chịu, xử lí hạt giống, dự tính dự báo bệnh, vệ sinh đồng ruộng, bón phân cân đối. – Có thể chủ động phun thuốc phòng bệnh khi trời âm u, độ ẩm cao, sương mù.

   Câu hỏi 7 trang 95 Công nghệ 10: Nêu sự khác nhau giữa các bước sản xuất chế phẩm vi khuẩn trừ sâu, chế phẩm virus trừ sâu và chế phẩm nấm trừ sâu, bệnh hại cây trồng.

   Trả lời:

   Khác nhau ở 4 bước đầu:

   	Chế phẩm vi khuẩn trừ sâu	Chế phẩm virus trừ sâu	Chế phẩm nấm trừ sâu, bệnh
   Bước 1	Sản xuất giống vi khuẩn cấp 1 từ giống vi khuẩn thuần chủng	Chuẩn bị giống virus thuần chủng. Nhân nuôi vật chủ	Sản xuất giống nấm cấp 1 từ nguồn nấm thuần chủng
   Bước 2	Sản xuất giống vi khẩn cấp 2 từ giống vi khuẩn cấp 1	Lây nhiễm virus lên vật chủ	Sản xuất giống nấm cấp 2 từ giống nấm cấp 1
   Bước 3	Lên men, tăng sinh khối vi khuẩn trong môi trường thích hợp	Nhân nuôi virus trên vật chủ để tăng sinh khối	Lên men, tăng sinh khối nấm trong môi trường thích hợp
   Bước 4	Sấy khô và nghiền vi khuẩn	Nghiền, lọc, li tâm lấy dịch	Sấy khô nấm

   Xem thêm các bài giải SGK Công nghệ 10 Kết nối tri thức hay, chi tiết khác:

   Bài 18: Ứng dụng công nghệ vi sinh trong phòng trừ sâu, bệnh hại cây trồng

   Ôn tập chương 5

   Bài 19: Quy trình trồng trọt và cơ giới hoá trong trồng trọt

   Bài 20: Công nghệ cao trong thu hoạch và bảo quản sản phẩm trồng trọt

   Bài 21: Chế biến sản phẩm trồng trọt