Lý thuyết Tính chất ba đường phân giác của tam giác (Cánh diều 2023) hay, chi tiết | Toán lớp 7

Lý thuyết Toán lớp 7 Bài 11: Tính chất ba đường phân giác của tam giác

A. Lý thuyết

1. Đường phân giác của tam giác

– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của $\widehat{\text{A}}$ cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

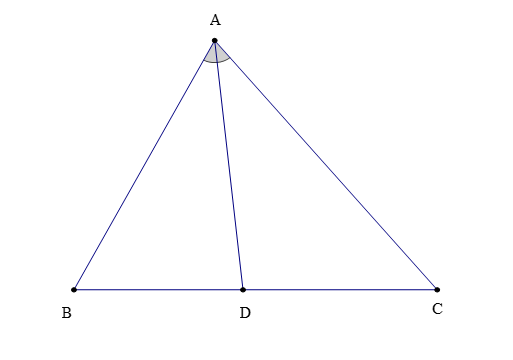
Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.

Ví dụ: Quan sát hình vẽ và chỉ ra các đường phân giác trong ∆ABC (nếu có):

Hướng dẫn giải

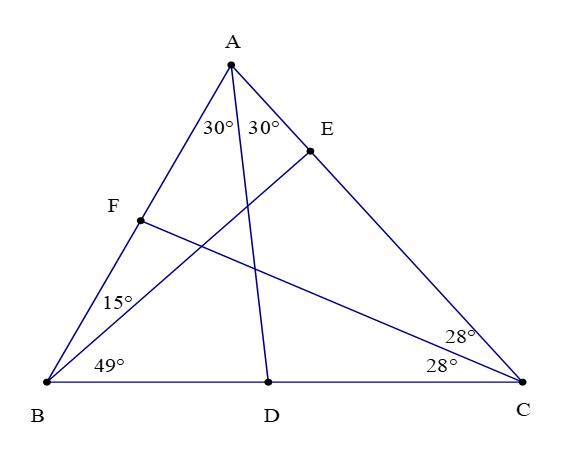
Quan sát hình vẽ trên, ta có:

$\widehat{\text{BAD}}=\widehat{\text{CAD}}=30°$ và D là giao điểm của tia phân giác $\widehat{\text{BAC}}$với cạnh BC. Do đó đoạn thẳng AD là đường phân giác của ∆ABC.

$\widehat{\text{ACF}}=\widehat{\text{FCB}}=28°$ và F là giao điểm của tia phân giác $\widehat{\text{ACB}}$với cạnh AB. Do đó đoạn thẳng CF là đường phân giác của ∆ABC.

Đoạn thẳng BE không là đường phân giác của ∆ABC vì BE không là tia phân giác của $\widehat{\text{ABC}}$ của tam giác ABC.

Nhận xét: Mỗi tam giác có ba đường phân giác.

Ví dụ:

∆ABC có ba đường phân giác AE; BF; CK xuất phát từ ba đỉnh của tam giác này.

2. Tính chất ba đường phân giác của tam giác

– Ba đường phân giác của một tam giác cùng đi qua một điểm

Nhận xét:

+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.

– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.

Ví dụ: Cho ∆DEF có I là giao điểm của ba đường phân giác. Kẻ IH ⊥ EF tại H ; IK ⊥ DF tại K. Chứng minh rằng: IF là đường trung trực của đoạn thẳng HK.

Hướng dẫn giải

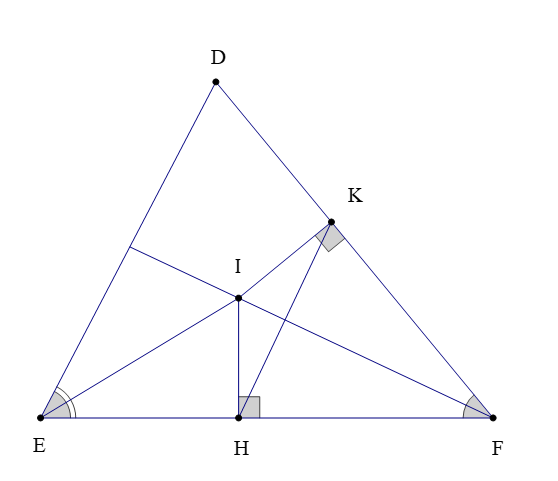
Theo bài ta có: IH ⊥ EF tại H; IK ⊥ DF tại K nên IH; IK lần lượt là khoảng cách từ điểm I tới cạnh EF và DF.

Mà I là giao điểm của ba đường phân giác của ∆DEF (giả thiết)

Do đó IH = IK (tính chất ba đường phân giác của tam giác)

Suy ra I nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng)   (1)

Xét ∆IKF và ∆IHF có:

$\widehat{\text{IKF}}=\widehat{\text{IHF}}=90°$ (IH ⊥ EF tại H ; IK ⊥ DF tại K),

IH = IK (chứng minh trên),

IF là cạnh chung.

Do đó ∆IKF = ∆IHF (cạnh huyền – cạnh góc vuông)

Suy ra FK = FH (hai cạnh tương ứng)

Suy ra F nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng)   (2)

Từ (1) và (2) suy ra I và F nằm trên đường trung trực của HK

Hay IF là đường trung trực của HK

Vậy IF là đường trung trực của  đoạn thẳng HK.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Cho ∆ABC các tia phân giác của $\widehat{\text{ABC}}$ và $\widehat{\text{BAC}}$ cắt nhau tại điểm O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho BM = 4 cm, CN = 5 cm. Tính độ dài đoạn thẳng MN.

Hướng dẫn giải

Vì O là giao điểm các tia phân giác của $\widehat{\text{ABC}}$ và $\widehat{\text{BAC}}$ nên CO là tia phân giác $\widehat{\text{ACB}}$

Suy ra $\widehat{\text{NCO}}=\widehat{\text{OCB}}$   (1)

Mà $\widehat{\text{NOC}}=\widehat{\text{OCB}}$ (hai góc so le trong vì MN // BC)   (2)

Từ (1) và (2) suy ra $\widehat{\text{NCO}}=\widehat{\text{NOC}}$ suy ra ∆NOC cân tại N.

Nên NO = NC.

Vì BO là phân giác của $\widehat{\text{ABC}}$ suy ra $\widehat{\text{MBO}}=\widehat{\text{OBC}}$  (3)

Do MN // BC nên $\widehat{\text{MOB}}=\widehat{\text{OBC}}$ (hai góc ở vị trí so le trong)  (4)

Từ (3) và (4) suy ra $\widehat{\text{MBO}}=\widehat{\text{MOB}}$ suy ra ∆MBO cân tại B

Suy ra MB = MO.

Ta có MN = MO + ON = MB + NC (vì NO = NC; MB = MO)

Hay MN = 4 + 5 = 9 (cm).

Vậy MN = 9 cm.

Bài 2. Cho ∆DEF cân tại D có $\widehat{\text{EDF}}=40°$ và DM là đường trung tuyến. Tia phân giác của $\widehat{\text{E}}$ cắt DM ở N. Tính $\widehat{\text{MFN}}$?

Hướng dẫn giải

Xét ∆DEF có $\widehat{\text{EDF}}+\widehat{\text{DEF}}+\widehat{\text{DFE}}=180°$(tổng ba góc trong một tam giác)

Hay $\widehat{\text{DEF}}+\widehat{\mathrm{DFE}}=180°-\widehat{\text{EDF}}=180°-40°=140°$

Ta lại có $\widehat{\text{DEF}}=\widehat{\text{DFE}}$(vì ∆DEF cân tại D)

Suy ra $\widehat{\text{DEF}}=\widehat{\text{DFE}}=\frac{140°}{2}=70°$

Xét DDEM và DDFM có:

DE = DF (vì ∆DEF cân tại D),

DM là cạnh chung,

EM = FM (do M là trung điểm của EF),

DM là cạnh chung.

Vậy DDEM = DDFM (c.c.c)

Suy ra $\widehat{\mathrm{EDM}}=\widehat{\mathrm{FDM}}$ (hai góc tương ứng)

Do đó DM là đường phân giác của $\widehat{\mathrm{EDF}}$.

Lại có EN là đường phân giác của $\widehat{\mathrm{DEF}}$

Mà DM cắt EN tại N.

Do đó FN là đường phân giác của tam giác DEF.

Suy ra $\widehat{\mathrm{DFN}}=\widehat{\mathrm{NFE}}=\frac{1}{2}\widehat{\mathrm{DFM}}$ (tính chất tia phân giác)

Mà $\widehat{\text{DFM}}=70°$

Suy ra $\widehat{\text{DFN}}=\widehat{\text{NFM}}=\frac{70°}{2}=35°$

Vậy $\widehat{\text{MFN}}=35°$.

Bài 3. Cho ∆ABC vuông tại A có I là giao điểm của ba đường phân giác trong tam giác. Gọi E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC. Chứng minh IE = IF = EA = FA.

Hướng dẫn giải

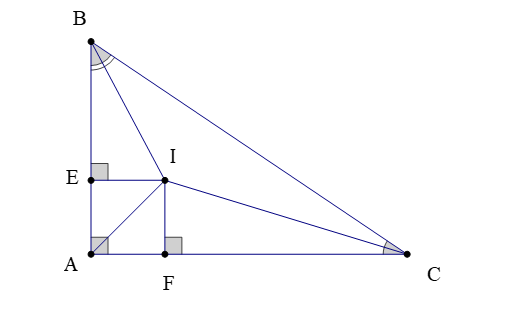
Theo bài ta có: I là giao điểm của ba đường phân giác trong ∆ABC.

Do đó AI là phân giác $\widehat{\text{BAC}}$ hay $\widehat{\text{EAF}}$.

Suy ra $\widehat{\text{EAI}}=\widehat{\text{FAI}}=\frac{1}{2}\widehat{\mathrm{BAC}}$  (tính chất tia phân giác)

Mà $\widehat{\mathrm{BAC}}=90°$ nên $\widehat{\text{EAI}}=\widehat{\text{FAI}}=\frac{90°}{2}=45°$

∆AEI vuông tại E có $\widehat{\text{EAI}}=45°$nên ∆AEI vuông cân tại E.

Suy ra EA = EI (tính chất tam giác cân)         (1)

∆AFI vuông tại F có $\widehat{\text{EAI}}=45°$ nên ∆AFI vuông cân tại F.

Suy ra FA = FI (tính chất tam giác cân)         (2)

Do I là giao điểm của ba đường phân giác trong ∆ABC và IE; IF lần lượt là khoảng cách từ I đến cạnh AB; AC (vì E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC)

Nên IE = IF (tính chất ba đường phân giác trong tam giác)  (3)

Từ (1), (2) và (3) suy ra IE = IF = EA = FA.

Vậy IE = IF = EA = FA.

B.2 Bài tập trắc nghiệm

Câu 1. Cho ∆ABC biết $\widehat{\mathrm{ABC}}=60°$, $\widehat{\mathrm{BAC}}=80°$. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác này. Số đo $\widehat{\mathrm{ICA}}$ bằng:

A. 40°;                  

B. 20°;                  

C. 30°;                  

D. 80°.

Hướng dẫn giải

Đáp án đúng là: B

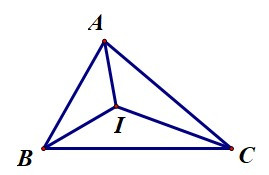
∆ABC có: $\widehat{\mathrm{ACB}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{BAC}}=180°$ (định lí tổng ba góc của tam giác)

Suy ra $\widehat{\mathrm{ACB}}=180°-\widehat{\mathrm{ABC}}-\widehat{\mathrm{BAC}}=180°-60°-80°=40°$.

Ta có I là điểm nằm trong tam giác và cách đều ba cạnh của ∆ABC (giả thiết).

Ta suy ra I là giao điểm của ba đường phân giác của ∆ABC.

Do đó $\widehat{\mathrm{ICA}}=\frac{1}{2}\widehat{\mathrm{ACB}}=\frac{1}{2}.40°=20°$.

Vậy ta chọn đáp án B.

Câu 2. Cho ∆ABC có AH vừa là đường cao, vừa là đường phân giác. Hỏi ∆ABC chắc chắn là tam giác gì?

A. Tam giác cân;             

B. Tam giác đều;             

C. Tam giác vuông;                   

D. Tam giác nhọn.

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABH và ∆ACH, có:

AH là cạnh chung.

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{AHC}}=90°$.

$\widehat{\mathrm{BAH}}=\widehat{\mathrm{CAH}}$ (do AH là đường phân giác của ∆ABC).

Do đó ∆ABH = ∆ACH (cạnh góc vuoogn – góc nhọn kề).

Suy ra AB = AC (cặp cạnh tương ứng).

Khi đó ∆ABC cân tại A.

Vì không có thêm dữ kiện nào để khẳng định tam giác ABC đều hay vuông hoặc nhọn nên ta chưa khẳng định được các đáp án B, C, D.

Vậy ta chọn đáp án A.

Câu 3. Cho ∆ABC có $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}$. Từ đỉnh A, kẻ đường cao AH và đường phân giác AD của ∆ABC. Số đo $\widehat{\mathrm{HAD}}$ bằng:

A. $\widehat{\mathrm{B}}-\widehat{\mathrm{C}}$;              

B. $\frac{\widehat{\mathrm{B}}+\widehat{\mathrm{C}}}{2}$;             

C. $\widehat{\mathrm{B}}+\widehat{\mathrm{C}}$;              

D. $\frac{\widehat{\mathrm{B}}-\widehat{\mathrm{C}}}{2}$.

Hướng dẫn giải

Đáp án đúng là: D

∆ABC có: $\widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{ACB}}=180°$ (định lí tổng ba góc của tam giác)

Suy ra $\widehat{\mathrm{BAC}}=180°-\widehat{\mathrm{ABC}}-\widehat{\mathrm{ACB}}$.

Vì AD là đường phân giác của ∆ABC.

Nên $\widehat{\mathrm{BAD}}=\widehat{\mathrm{CAD}}=\frac{\widehat{\mathrm{BAC}}}{2}=\frac{180°-\widehat{\mathrm{ABC}}-\widehat{\mathrm{ACB}}}{2}$.

∆ABH vuông tại H: $\widehat{\mathrm{ABH}}+\widehat{\mathrm{BAH}}=90°$.

Suy ra $\widehat{\mathrm{BAH}}=90°-\widehat{\mathrm{ABC}}$.

Ta có $\widehat{\mathrm{HAD}}=\widehat{\mathrm{BAD}}-\widehat{\mathrm{BAH}}$

$=\frac{180°-\widehat{\mathrm{ABC}}-\widehat{\mathrm{ACB}}}{2}-\left(90°-\widehat{\mathrm{ABC}}\right)$

$=\frac{180°}{2}-\frac{\widehat{\mathrm{ABC}}}{2}-\frac{\widehat{\mathrm{ACB}}}{2}-90°+\widehat{\mathrm{ABC}}$

$=90°+\frac{\widehat{\mathrm{ABC}}}{2}-\frac{\widehat{\mathrm{ACB}}}{2}-90°$

$=\frac{\widehat{\mathrm{ABC}}-\widehat{\mathrm{ACB}}}{2}=\frac{\widehat{\mathrm{B}}-\widehat{\mathrm{C}}}{2}$.

Vì vậy $\widehat{\mathrm{HAD}}=\frac{\widehat{\mathrm{B}}-\widehat{\mathrm{C}}}{2}$.

Vậy ta chọn đáp án D.

====== ****&**** =====