50 Bài tập Ôn tập và bổ sung về giải toán (tiếp) (có đáp án)- Toán 5

Bài tập Toán 5 Chương 1 Bài 11: Ôn tập và bổ sung về giải toán

A. Bài tập Ôn tập và bổ sung về giải toán

I. Bài tập trắc nghiệm

Câu 1: Lan mua 3 cái bút hết 12 000 đồng. Nếu Lan mua 6 cái bút hết 24 000 đồng. Hỏi hai đại lượng “số cái bút” và “số tiền” có quan hệ gì với nhau?

A. Là hai đại lượng tỉ lệ thuận

B.  Là hai đại lượng tỉ lệ nghịch

Câu 2: Mua 4m vải hết 96 000 đồng. Hỏi mua 8m vải như thế hết bao nhiêu tiền?

A. 24 000 đồng

B. 48 000 đồng

C. 192 000 đồng

D. 768 000 đồng

Câu 3: Bạn Lan mua 5 cái bút chì hết 15 000 đồng. Hỏi bạn Nam muốn mua 7 cái bút chì như thế thì phải trả người bán hàng bao nhiêu tiền?

A. 21 000 đồng

B. 24 000 đồng

C. 25 000 đồng

D. 30 000 đồng

Câu 4: Muốn xây xong một cái bể trong 4 ngày thì cần có 6 người. Hỏi muốn xây xong cái bể đó trong 3 ngày thì cần bao nhiêu người?

A. 4 người

B. 10 người

C. 12 người

D. 8 người

Câu 5: May 5 bộ quần áo hết 15m vải. Hỏi may 30 bộ quần áo như thế thì hết bao nhiêu mét vải?

A. 75m

B. 90m

C. 150m

D. 450m

Câu 6: Một xe tải chỉ có thể chở được 75 bao gạo, mỗi bao 40kg. Nếu chất lên xe đó loại 50kg 1 bao thì xe chở được nhiều nhất bao nhiêu bao?

A. 60 bao

B. 62 bao

C. 64 bao

D. 66 bao

Câu 7: Một bếp ăn dự trữ gạo đủ cho 84 người ăn trong 20 ngày. Nếu chỉ có 60 người ăn thì số gạo đó đủ dùng trong bao nhiêu ngày?

A. 1680 ngày

B. 72 ngày

C. 28 ngày

D. 14 ngày

Câu 8: Số dân ở một xã hiện nay là 6000 người.

a) Với mức tăng hằng năm là cứ 1000 người thì tăng thêm 27 người thì một năm sau số dân của xã đó là … người.

b) Nếu hạ mức tăng hàng năm xuống là cứ 1000 người thì tăng thêm 22 người thì một năm sau số dân của xã đó là … người

Số thích hợp điền vào chỗ chấm từ trên xuống dưới lần lượt là:

A. $6152;6122$

B. $6162;6132$

C. $6027;6022$

D. $6242;6122$

II. Bài tập tự luận

Câu 1: Một người làm trong 3 ngày được nhận 525 000 đồng tiền công. Hỏi với mức trả công như thế, nếu làm trong 7 ngày thì người đó nhận được bao nhiêu tiền công?

Câu 2: 5 người làm xong một công việc phải hết 14 ngày. Nay muốn làm xong công việc đó trong 10 ngày thì cần bổ sung thêm bao nhiêu người?

Câu 3: Một đội 12 người trong một ngày trồng được 125 cây xanh. Người ta bổ sung thêm 24 người nữa thì trong một ngày đội đó trồng được tất cả bao nhiêu cây xanh?

Câu 4: Một gia đình gồm 3 người (bố, mẹ và một con). Bình quân thu nhập hàng tháng là 1 600 000 đồng mỗi người. Nếu gia đình đó có thêm một con nữa mà tổng thu nhập của gia đình không thay đổi thì bình quân thu nhập hàng tháng của mỗi người bị giảm đi bao nhiêu tiền?

Câu 5: Một bếp ăn dự trữ gạo đủ cho 172 người ăn trong 30 ngày. Nhưng sau đó có một số người đến thêm nên số gạo chỉ đủ ăn trong 24 ngày. Hỏi có bao nhiêu người đến thêm?

III. Bài tập vận dụng

Câu 1: Để hút hết nước ở một cái hồ, người ta phải dùng 4 máy bơm làm việc liên tục trong 10 giờ. Vì muốn công việc hoàn thành sớm hơn nên người ta đã dùng 8 máy bơm như thế. Hỏi sau mấy giờ sẽ hút hết nước ở hồ đó?

A. 4 giờ

B. 5 giờ

C. 12 giờ

D. 20 giờ

Đáp án

(Phương pháp rút về đơn vị)

Một máy bơm hút hết số nước ở hồ sau số giờ là:

10 x 4 = 40 (giờ)

Nếu dùng 8 máy bơm thì sẽ hút hết nước ở hồ đó sau số giờ là:

40 : 8 = 5 (giờ)

Đáp số: 5 giờ.

(Phương pháp dùng tỉ số)

8 máy bơm gấp 4 máy bơm số lần là:

8 : 4 = 2 (lần)

Nếu dùng 8 máy bơm thì sẽ hút hết nước ở hồ đó sau số giờ là:

10 : 2 = 5 (giờ)

Đáp số: 5 giờ.

Câu 2: Bác Lan mua (8kg ) táo hết (120000 ) đồng. Hỏi nếu bác mua (15kg ) táo như vậy thì hết bao nhiêu tiền?

A. 180000 đồng

B. 64000 đồng

C. 225000 đồng

D. 2250000 đồng

Đáp án

(Phương pháp rút về đơn vị)

Bác Lan mua 1kg táo hết số tiền là:

120000 : 8 = 15000 (đồng)

Nếu bác mua 15kg táo như vậy thì hết số tiền là:

15000 x 15 = 225000 (đồng)

Đáp số: 225000 đồng.

(Phương pháp dùng tỉ số)

15kg táo gấp 8kg táo số lần là:

15 : 8 =  (lần)

Nếu bác mua 15kg táo như vậy thì hết số tiền là:

120000 x  = 225000 (đồng)

Đáp số: 225000 đồng.

Câu 3: Đội tuyển học sinh giỏi có 18 học sinh nam và 22 học sinh nữ. Tính tỉ số phần trăm của số học sinh nữ và số học sinh cả đội tuyển.Đội tuyển học sinh giỏi có 18 học sinh nam và 22 học sinh nữ. Tính tỉ số phần trăm của số học sinh nữ và số học sinh cả đội tuyển.

A. 55%

B. 45%

C. 81%

D. 122%

Đáp án

Đội tuyển học sinh giỏi có tất cả số học sinh là:

18 + 22 = 40 (bạn)

Tỉ số phần trăm của số học sinh nữ và số học sinh cả đội tuyển là:

22 : 40 = 0,55

0,55 = 55%

Đáp số: 55%

Câu 4: Một ô tô khởi hành từ tỉnh A lúc 6 giờ 30 phút và đến tỉnh B lúc 10 giờ. Tỉnh A cách tỉnh B 168km. Tính vận tốc ô tô, biết dọc đường ô tô dừng lại nghỉ 10 phút.

A. 45,8 km/giờ

B. 48 km/giờ

C. 55,5 km/giờ

D. 50,4 km/giờ

Đáp án

Thời gian ô tô đi từ A đến B tính cả thời gian nghỉ là:

10 giờ − 6 giờ 30 phút = 3 giờ 30 phút

Thời gian ô tô đi từ A đến B không tính thời gian nghỉ là:

3 giờ 30 phút − 10 phút = 3 giờ 20 phút

Đổi 3 giờ 20 phút =  giờ =  giờ

Vận tốc của ô tô là:

168 :  = 50,4 (km/giờ)

Đáp số: 50,4 km/giờ.

Câu 5: Điền số thích hợp vào ô trống:

Một cửa hàng đường trong ba ngày, trung bình mỗi ngày cửa hàng bán được 4 tạ đường. Ngày đầu cửa hàng bán được 468kg đường, ngày thứ hai cửa hàng bán được 75% số đường bán được trong ngày đầu.

Vậy ngày thứ ba cửa hàng bán được  ki-lô-gam đường.

Đáp án

Trong ba ngày, cửa hàng bán được số đường là:

4 x 3 = 12 (tạ)

Đổi 12 tạ = 1200kg

Ngày thứ hai cửa hàng bán được số ki-lô-gam đường là:

468 : 100 x 75 = 351 (kg)

Ngày thứ ba cửa hàng bán số ki-lô-gam đường là:

1200 – (468 + 351) = 381 (kg)

Đáp số: 381kg đường.

Vậy đáp án đúng điền vào ô trống là 381.

B. Lý thuyết Ôn tập và bổ sung về giải toán

1. Tìm hai số khi biết tổng và hiệu của hai số đó

* Phương pháp giải:

+ Bước 1: Vẽ sơ đồ tóm tắt đề bài

+ Bước 2: Tìm số bé và số lớn theo công thức:

Số lớn = (Tổng + Hiệu) : 2

Số bé = (Tổng – Hiệu) : 2

+ Bước 3: Kết luận (hay đáp số)

Ví dụ: Tổng hai số là 71 và hiệu hai số đó là 13. Tìm hai số đó.

Bài làm

Ta có sơ đồ:

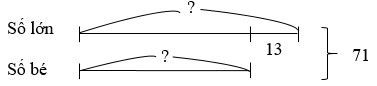
Số lớn là:

(71 + 13) : 2 = 42

Số bé là:

71 – 42 = 29

Đáp số: số bé: 29; số lớn: 42

2. Tìm tỉ số của hai số

* Định nghĩa: Tỉ số của hai số a và b là a : b hay  (b khác 0)

Ví dụ: Tỉ số của hai số 3 và 5 là .

* Lưu ý: Muốn lập tỉ số của hai đơn vị đo đại lượng thì chúng phải cùng đơn vị đo.

Ví dụ: Tìm tỉ số của hai đoạn thẳng có độ dài là 1dm và 12cm.

Lời giải:

Đổi 1dm = 10cm

Tỉ số của hai đoạn thẳng trên là: 

3. Tìm hai số khi biết tổng và tỉ số của hai số đó

* Phương pháp giải:

+ Bước 1: Vẽ sơ đồ tóm tắt bài toán

+ Bước 2: Trình bày bài toán theo các bước:

– Tìm tổng số phần bằng nhau.

– Tìm giá trị một phần (lấy tổng ban đầu chia tổng số phần bằng nhau).

– Tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn

+ Bước 3: Kết luận (hay đáp số).

Ví dụ: Cho hai số có tổng là 63. Tìm hai số đó, biết rằng tỉ số của hai số là 4/5.

 Bài làm

Ta có sơ đồ:

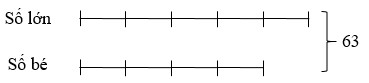
Theo sơ đồ, tổng số phần bằng nhau là:

4 + 5 = 9 (phần)

Giá trị một phần là:

63 : 9 = 7

Số bé là:

7 x 4 = 28

Số lớn là:

63 – 28 = 35

Đáp số: số bé: 28; số lớn: 35

4. Tìm hai số khi biết hiệu và tỉ số của hai số đó

* Phương pháp giải:

+ Bước 1: Vẽ sơ đồ tóm tắt bài toán

+ Bước 2: Trình bày bài toán theo các bước:

– Tìm hiệu số phần bằng nhau.

– Tìm giá trị một phần (lấy hiệu ban đầu chia hiệu số phần bằng nhau).

– Tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn

+ Bước 3: Kết luận (hay đáp số)

Ví dụ: Tìm hai số khi biết hiệu của hai số là 52 và tỉ số của hai số đó là 3/7.

Bài làm

Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:

7 – 3 = 4 (phần)

Giá trị một phần là:

52:4 = 13

Số lớn là:

13 x 7 = 91

Số bé là:

91 – 52 = 39

Đáp số: Số bé: 39; số lớn: 91