Một phân xưởng được giao nhiệm vụ sản xuất một số lượng sản phẩm trong thời gian 10 ngày. Do cải tiến kĩ thuật, mỗi ngày phân xưởng sản xuất nhiều hơn dự định 20 sản phẩm nên không những hoàn thành kế hoạch sớm hơn 2 ngày mà còn làm vượt mức 40 sản phẩm. Tính năng suất dự định của phân xưởng.

By 0

Câu hỏi:

Một phân xưởng được giao nhiệm vụ sản xuất một số lượng sản phẩm trong thời gian 10 ngày. Do cải tiến kĩ thuật, mỗi ngày phân xưởng sản xuất nhiều hơn dự định 20 sản phẩm nên không những hoàn thành kế hoạch sớm hơn 2 ngày mà còn làm vượt mức 40 sản phẩm. Tính năng suất dự định của phân xưởng.

Trả lời:

Gọi x là năng suất dự định của phân xưởng (x > 0), (sản phẩm/ngày).Số sản phẩm phân xưởng được giao nhiệm vụ sản xuất là 10x (sản phẩm).Năng suất thực tế là: x + 20 (sản phẩm/ngày)Thời gian thực tế là: 10 – 2 = 8 (ngày)Sản phẩm thực tế là: 8(x + 20) (sản phẩm).Vì thực tế phân xưởng làm vượt mức 40 sản phẩm nên ta có phương trình:Vậy năng suất dự định của phân xưởng là 100 (sản phẩm/ngày).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. a) Phân tích nhân tử i) xy – 6y + 2x – 12  ii) 2x(y – z) + (z – y)(x + y)  b) Tìm x biết: x + 3 = x + 32 

    Câu hỏi:

    a) Phân tích nhân tử i) xy – 6y + 2x – 12  ii) 2x(y – z) + (z – y)(x + y)  b) Tìm x biết: x + 3 = x + 32 

    Trả lời:

    i) xy – 6y + 2x – 12= (xy – 6y) + (2x – 12)= y(x – 6) + 2(x – 6)= (x – 6)(y + 2)ii) 2x(y – z) + (z – y)(x + y)= 2x(y – z) – (y – z)(x + y)= (y – z)(2x – x – y)= (y – z)(x – y)b) x + 3 = (x + 3)2 ⇔ (x + 3)2 – (x + 3) = 0 ⇔ (x + 3)(x + 3 – 1) = 0⇔ (x + 3)(x + 2) = 0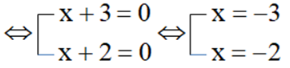Vậy x = -3; x = -2

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Rút gọn và tính giá trị của biểu thức: A=2×1-x3+1×2-x+1×2+x+1 khi x = 10

    Câu hỏi:

    Rút gọn và tính giá trị của biểu thức: A=2x1–x3+1x2–x+1x2+x+1 khi x = 10

    Trả lời:

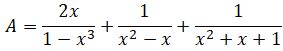
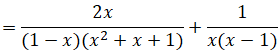
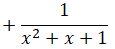
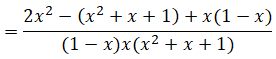
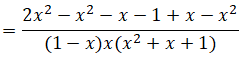
    Điều kiện: x ≠ 1; x ≠ 0.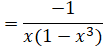Khi x = 10 ta có: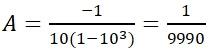 

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. Cho biểu thức: P=2×4-1-11-x2a) Tìm điều kiện xác định của biểu thức P.b) Chứng minh giá trị của P luôn âm với x ≠ ±1

    Câu hỏi:

    Cho biểu thức: P=2x4–1–11–x2a) Tìm điều kiện xác định của biểu thức P.b) Chứng minh giá trị của P luôn âm với x ≠ ±1

    Trả lời:

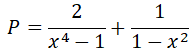
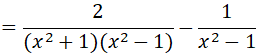
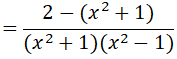
    a) Ta có: x4 – 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.Vậy điều kiện : x2 – 1 ≠ 0x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1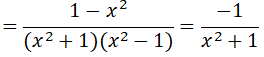Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Chứng minh rằng biểu thức Q=x2-11x-1-1x+1+1 luôn dương với x≠±1

    Câu hỏi:

    Chứng minh rằng biểu thức Q=x2–11x–1–1x+1+1 luôn dương với x≠±1

    Trả lời:

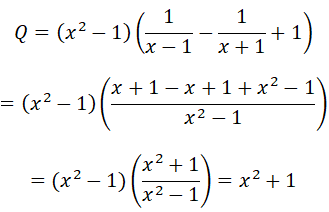    Do x2≥ 0 ∀ x ≠ ±1 nên Q=x2 + 1 ≥ 1 ∀ x ≠ ±1

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.Chứng minh tứ giác ANCE là hình thoi.c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.

    Câu hỏi:

    Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.Chứng minh tứ giác ANCE là hình thoi.c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.

    Trả lời:

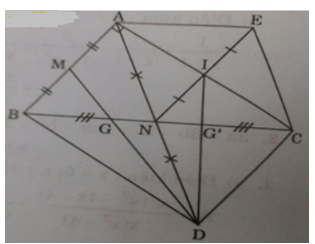    a) Ta có: NB = NC (gt); ND = NA (gt)⇒ Tứ giác ABDC là hình bình hànhcó ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.b) Ta có: AI = IC (gt); NI = IE (gt)⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.Vậy tứ giác AECN là hình thoi.c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.Tương tự G’ là trọng tâm của hai tam giác ACD⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)Lại có: BG = GG’ = CG’ (tính chất trọng tâm)⇒ SDGB = SDGG’ = SDG’C = 1/3 SBCD(chung đường cao kẻ từ D và đáy bằng nhau)Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))⇒SDGG’ = 24/3 = 8(cm2)

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu