Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b. – Em có thể ghép bốn tứ giác khít nhau như vậy không? – Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo

By 0

Câu hỏi:

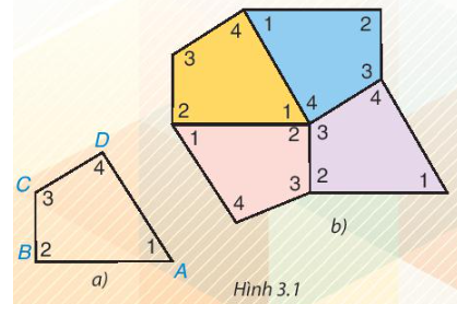
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
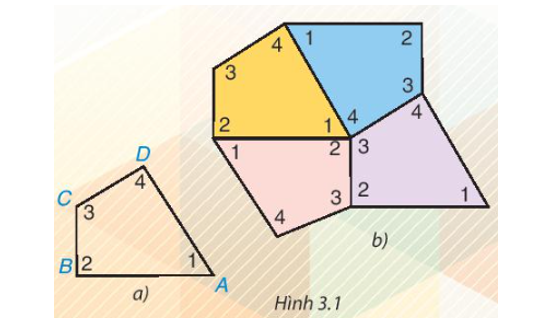
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong (ảnh 1)
– Em có thể ghép bốn tứ giác khít nhau như vậy không?
– Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo

Trả lời:

– Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
 – Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó:  A^+B^+C^+D^=360°

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.

    Câu hỏi:

    Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.
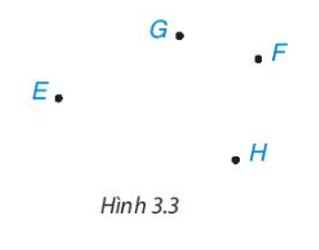
    Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho. (ảnh 1)

    Trả lời:

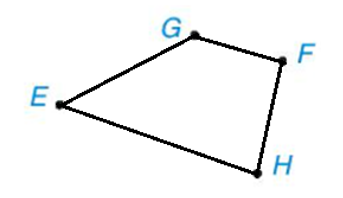
    Nối EG, GF, FH, HE, ta được tứ giác EGFH như hình vẽ.
    Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho. (ảnh 2)

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Quan sát tứ giác ABCD trong Hình 3.4. – Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại. – Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại. – Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

    Câu hỏi:

    Quan sát tứ giác ABCD trong Hình 3.4.
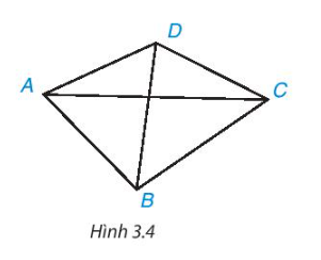
    Quan sát tứ giác ABCD trong Hình 3.4. - Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau (ảnh 1)
    – Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.
    – Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.
    – Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

    Trả lời:

    – Đường chéo còn lại của tứ giác ABCD là BD.
    – Cặp cạnh đối còn lại của tứ giác ABCD là cặp cạnh AB và CD.
    – Cặp góc đối còn lại của tứ giác ABCD là cặp góc B và D.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

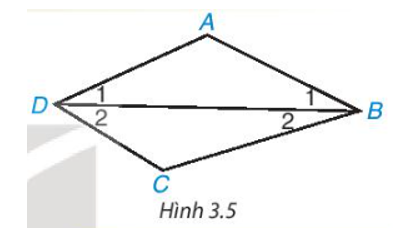
  3. Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng  của tứ giác ABCD.

    Câu hỏi:

    Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng  của tứ giác ABCD.
    Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong (ảnh 1)

    Trả lời:

    Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
    A^+B^1+D^1=180°
    C^+B^2+D^2=180°
    Khi đó, tứ giác ABCD có:
    A^+B^+C^+D^=A^+B^1+D^1+C^+B^2+D^2=180°+180°=360°
    Vậy A^+B^+C^+D^=360°

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

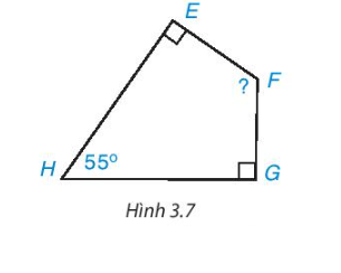
  4. Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F

    Câu hỏi:

    Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F
    Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F (ảnh 1)

    Trả lời:

    Xét tứ giác EFGH có:
    E^+F^+G^+H^=360° (định lí tổng các góc trong một tứ giác).
    Hay 90°+F^+90°+55°=360°
    Suy ra F^+235°=360°
    Do đó F^=360°−235°=125°.
    Vậy F^=125°.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b – Em có thể ghép bốn tứ giác khít nhau như vậy không? – Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

    Câu hỏi:

    Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b
    Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD (ảnh 1)
    – Em có thể ghép bốn tứ giác khít nhau như vậy không?
    – Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

    Trả lời:

    – Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
    Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
    – Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
    Khi đó: A^+B^+C^+D^=360°.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu