Hình chóp S.ABCD đáy là hình vuông cạnh a, SD = a13/2. Hình chiếu của S lên (ABCD) là trung điểm H của AB. Thể tích khối chóp là

Câu hỏi:

Hình chóp S.ABCD đáy là hình vuông cạnh a, SD = a$\sqrt{13}$/2. Hình chiếu của S lên (ABCD) là trung điểm H của AB. Thể tích khối chóp là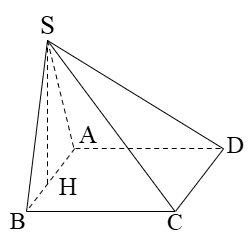

A. $\frac{{\mathrm{a}}^3\sqrt{2}}{3}$

Đáp án chính xác

B. $\frac{2{\mathrm{a}}^3}{3}$

C. ${\mathrm{a}}^3\sqrt{12}$

D. $\frac{{\mathrm{a}}^3}{3}$

Trả lời:

Đáp án A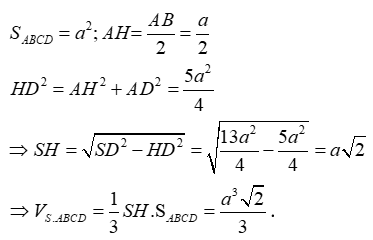

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3a/4. Thể tích của hình chóp S.ABC là:  
   
   

   Câu hỏi:
   

   Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng $\sqrt{3}$a/4. Thể tích của hình chóp S.ABC là:
    

   A. $\mathrm{V}=\frac{\sqrt{3}}{8}{\mathrm{a}}^3$

   B. $\mathrm{V}=\frac{\sqrt{2}}{12}{\mathrm{a}}^3$

   C. $\mathrm{V}=\frac{\sqrt{3}}{12}{\mathrm{a}}^3$

   D. $\mathrm{V}=\frac{\sqrt{3}}{24}{\mathrm{a}}^3$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   
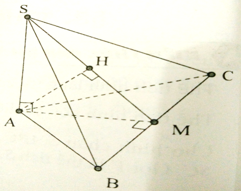
   Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:
   

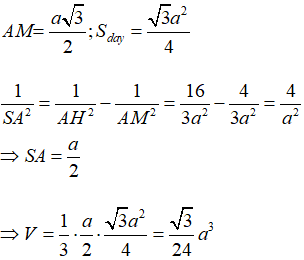
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a2. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.  
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a$\sqrt{2}$. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V’/V.
    

   A. $k=\frac{1}{3}$

   B. $k=\frac{\sqrt{2}}{4}$

   C. $k=\frac{4}{9}$

   Đáp án chính xác

   D. $k=\frac{2}{3}$

   Trả lời:

   Đáp án C
   
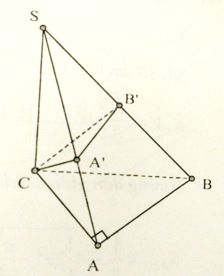
   Do CS = CB nên B’ là trung điểm của SB.
   Ta có:
   

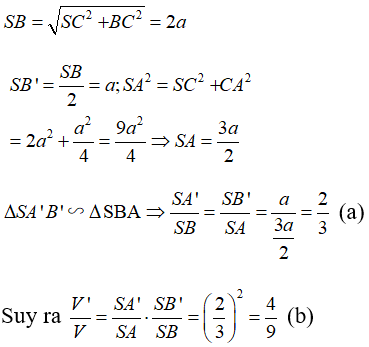
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a2. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a$\sqrt{2}$. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.

   A. $\mathrm{V}=\frac{\sqrt{14}}{54}{\mathrm{a}}^3$

   Đáp án chính xác

   B. $\mathrm{V}=\frac{\sqrt{14}}{64}{\mathrm{a}}^3$

   C. $\mathrm{V}=\frac{\sqrt{14}}{49}{\mathrm{a}}^3$

   D. $\mathrm{V}=\frac{4}{61}{\mathrm{a}}^3$

   Trả lời:

   Đáp án A
   
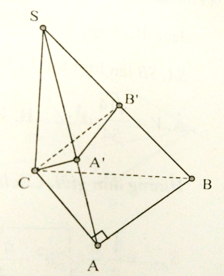
   Áp dụng ví dụ 2, ta có:
   
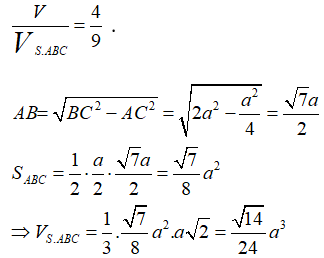
   Từ đó suy ra
   

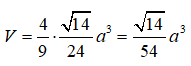
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a2, tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4a3/3. Tính khoảng cách h từ B đến mặt phẳng (SCD).  
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a$\sqrt{2}$, tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4${\mathrm{a}}^3$/3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
    

   A. $\mathrm{h}=\frac{2}{3}\mathrm{a}$

   B. $\mathrm{h}=\frac{4}{3}\mathrm{a}$

   Đáp án chính xác

   C. $\mathrm{h}=\frac{8}{3}\mathrm{a}$

   D. $\mathrm{h}=\frac{3}{4}\mathrm{a}$

   Trả lời:

   Đáp án B
   
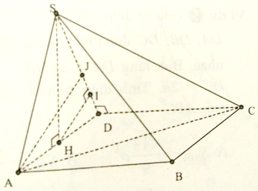
   Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
   Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
   Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
   Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
   Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
   Ta có
   
    
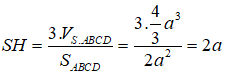
   Ta lại có
   

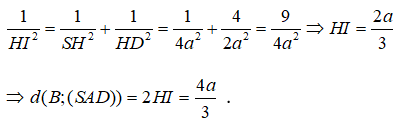
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = a2, DC = 2a. Tính diện tích S của tam giác ABC.  
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = a$\sqrt{2}$, DC = 2a. Tính diện tích S của tam giác ABC.
    

   A. ${\mathrm{S}}_{\mathrm{ABC}}=\frac{\sqrt{14}}{9}{\mathrm{a}}^2$

   B. ${\mathrm{S}}_{\mathrm{ABC}}=\frac{\sqrt{14}}{6}{\mathrm{a}}^2$

   C. ${\mathrm{S}}_{\mathrm{ABC}}=\frac{14}{4}{\mathrm{a}}^2$

   D. ${\mathrm{S}}_{\mathrm{ABC}}=\frac{\sqrt{14}}{2}{\mathrm{a}}^2$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   
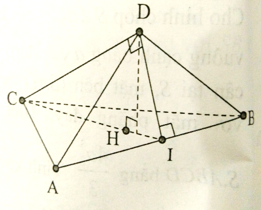
   Kẻ DI ⊥ AB, DH ⊥ CI. Khi đó DH ⊥ (BCA).
   Suy ra
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====