Câu hỏi:
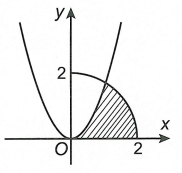
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y = \sqrt 3 {x^2}\), cung tròn có phương trình \(y = \sqrt {4 – {x^2}} \) (với \(0 \le x \le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) là
A. \(\frac{{4\pi + \sqrt 3 }}{{12}}\).
B. \(\frac{{4\pi – \sqrt 3 }}{6}\)
Đáp án chính xác
C. \(\frac{{4\pi + 2\sqrt 3 – 3}}{6}\).
D. \(\frac{{5\sqrt 3 – 2\pi }}{3}\).
Trả lời:
Hướng dẫn giải
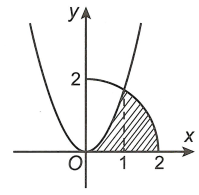
Phương trình hoành độ giao điểm của parabol \(y = \sqrt 3 {x^2}\) và cung tròn \(y = \sqrt {4 – {x^2}} \) (với \(0 \le x \le 2\)) lả \(\sqrt {4 – {x^2}} = \sqrt 3 {x^2} \Leftrightarrow 4 – {x^2} = 3{x^4} \Leftrightarrow x = 1\).
Diện tích của \(\left( H \right)\) là
\(S = \int\limits_0^1 {\sqrt 3 {x^2}dx} + \int\limits_1^2 {\sqrt {4 – {x^2}} dx} = \frac{{\sqrt 3 }}{3}{x^3}\left| \begin{array}{l}^1\\_0\end{array} \right. + I = \frac{{\sqrt 3 }}{3} + I\) với \(I = \int\limits_1^2 {\sqrt {4 – {x^2}} dx} \).
Đặt \(x = 2\sin t\), \(t \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = 2\cos t.dt\)
Đổi cận \(x = 1 \Rightarrow t = \frac{\pi }{6}\), \(x = 2 \Rightarrow t = \frac{\pi }{2}\).
\(I = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\sqrt {4 – 4{{\sin }^2}t} .2\cos t.dt} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {4{{\cos }^2}t.dt} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {2\left( {1 + \cos 2t} \right).dt} = \left( {2x + \sin 2t} \right)\left| \begin{array}{l}^{\frac{\pi }{2}}\\_{\frac{\pi }{6}}\end{array} \right.\)
\( = \frac{{2\pi }}{3} – \frac{{\sqrt 3 }}{2}\)
Vậy \(S = \frac{{\sqrt 3 }}{3} + I = \frac{{\sqrt 3 }}{3} + \frac{{2\pi }}{3} – \frac{{\sqrt 3 }}{2} = \frac{{4\pi – \sqrt 3 }}{6}\)
Chọn B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====