Cho hình lăng trụ BC.A’B’C’ có thể tích V. Lấy điểm I thuộc cạnh CC’ sao cho CI = 4CI’. Gọi M, N lần lượt là điểm đối xứng của A’, B’ qua I. Gọi V’ là thể tích của khối đa diện CABMNC’. Tỉ số VV’ bằng: 

Câu hỏi:

Cho hình lăng trụ BC.A’B’C’ có thể tích V. Lấy điểm I thuộc cạnh CC’ sao cho CI = 4CI’. Gọi M, N lần lượt là điểm đối xứng của A’, B’ qua I. Gọi V’ là thể tích của khối đa diện $CABMNC‘.$ Tỉ số $\frac{V}{V‘}$ bằng: 

A. $\frac{5}{9}$

B. $\frac{3}{4}$

Đáp án chính xác

C. $\frac{3}{10}$

D. $\frac{5}{8}$

Trả lời:

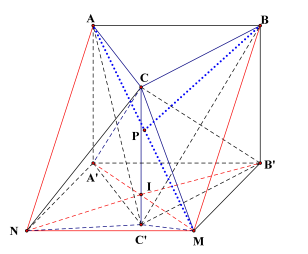
Gọi V, V’ lần lượt là thể tích khối lăng trụ ABC.A’B’C’ và khối đa diện $CABMNC‘.$

Gọi $P=AM\cap CC‘.$
Vì I là trung điểm của A’M và B’N nên ABMN là hình bình hành và A, B, M, N đồng phẳng.
Ta có AA’//CC’, mà I là trung điểm của A’M nên P là trung điểm của AM (1)
Lại có BB’//CC’ mà I là trung điểm của B’N nên P là trung điểm của BN (2)
Từ (1) và $\left(2\right)\Rightarrow P\in \left(ABMN\right).$
$\Rightarrow PC‘=PI+IC‘=\frac{AA‘}{2}+\frac{CC‘}{5}=\frac{CC‘}{2}+\frac{CC‘}{5}=\frac{7CC‘}{10}$
$\Rightarrow \frac{CP}{CC‘}=\frac{3}{10}$
$\Rightarrow \frac{V_{C.ABMN}}{V_{C‘.ABMN}}=\frac{d\left(C;\left(ABMN\right)\right)}{d\left(C‘;\left(ABMN\right)\right)}=\frac{CP}{CC‘}=\frac{3}{7}\Rightarrow V_{C‘.ABMN}=\frac{7}{3}{V}_{C.ABMN}$
 
Ta có: $\frac{V_{C.ABP}}{V_{C.ABC}}=\frac{CP}{CC‘}=\frac{3}{10}\Rightarrow V_{C.ABP}=\frac{3}{10}.V_{C.ABC‘}=\frac{3}{10}.\frac{V}{3}=\frac{V}{10}.$
$\left\{\begin{array}{l}{V}_{C.ABMN}=2V_{C.ABM}=4V_{C.ABP}=4.\frac{V}{10}=\frac{2V}{5}\\ V_{C‘.ABMN}=\frac{7}{3}{V}_{C.ABMN}=\frac{7}{3}.\frac{2V}{5}=\frac{14V}{15}\end{array}\right.$

$V‘=V_{CABMNC‘}=V_{C‘.ABMN}+V_{C.ABMN}=\frac{14V}{15}+\frac{2V}{5}=\frac{4}{3}V$
Vậy $\frac{V}{V‘}=\frac{3}{4}.$
Chọn B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số y=ax−bx−1 có đồ thị như hình vẽ bên:      Tích ab bằng:
   
   

   Câu hỏi:
   

   Cho hàm số $y=\frac{ax-b}{x-1}$ có đồ thị như hình vẽ bên:
   
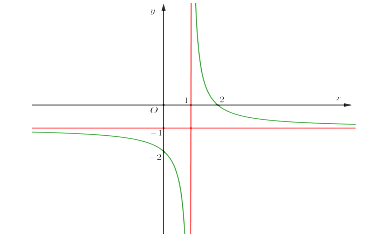
        Tích ab bằng:

   A. 2

   Đáp án chính xác

   B. -3

   C. -2

   D. 3

   Trả lời:

   Phương pháp:
   Dựa vào các đường tiệm cận và các điểm thuộc đồ thị hàm số.
   Cách giải:
   Đồ thị hàm số có TCN 
   Điểm  thuộc đồ thị hàm số nên ta có  do đó
   Vậy
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Hình đa diện nào sau đây có tâm đối xứng?
   
   

   Câu hỏi:
   

   Hình đa diện nào sau đây có tâm đối xứng?

   A. Hình lăng trụ tam giác đều                        

   B. Hình tứ diện đều

   C. Hình chóp tứ giác đều                                                                     

   D. Hình lập phương

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   Dựa vào khái niệm tâm đối xứng của khối đa diện.
   Cách giải:
   Hình đa diện có tâm đối xứng trong các đáp án đã cho là hình lập phương.
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và có thể tích bằng 3a3. Tính chiều cao h của khối chóp đã cho.
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và có thể tích bằng $\sqrt{3}{a}^3.$ Tính chiều cao h của khối chóp đã cho.

   A. $h=\frac{3\sqrt{3}a}{2}$

   B. $h=\frac{\sqrt{3}a}{3}$

   C. h = 3a

   Đáp án chính xác

   D. $h=2\sqrt{3}a$

   Trả lời:

   Phương pháp:
   Sử dụng công thức tính thể tích chóp $V=\frac{1}{3}{S}_{day}h\Rightarrow h=\frac{3V}{S_{day}}$
   Cách giải:
   Chiều cao của khối chóp là $h=\frac{3V}{S_{day}}=\frac{3.\sqrt{3}{a}^3}{\frac{{\left(2a\right)}^2\sqrt{3}}{4}}=3a.$
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Một khối trụ có diện tích xung quanh bằng 80π. Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10. 
   
   

   Câu hỏi:
   

   Một khối trụ có diện tích xung quanh bằng $80\pi .$ Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10. 

   A. $160\pi$

   Đáp án chính xác

   B. $40\pi$

   C. $64\pi$

   D. $400\pi$

   Trả lời:

   Phương pháp:
   – Diện tích khối trụ có chiều cao h bán kính đáy r là $S_{xq}=2\pi rh$, từ đó tính bán kính đáy của hình trụ.
   – Thể tích khối trụ có chiều cao h bán kính đáy r là $V=\pi r^{2}h.$
   Cách giải:
   Vì khoảng cách giữa hai đáy bằng 10 $\Rightarrow$ Chiều cao của hình trụ h = 10.
   Gọi r là bán kính đáy hình trụ ta có $S_{xq}=2\pi rh=80\pi \iff r=4.$
   Vậy thể tích khối trụ là $V=\pi r^{2}h=\pi {.4}^2.10=160\pi .$
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình S:x2+y2+z2−2x−4y−6z+5=0. Tính diện tích mặt cầu (S)
   
   

   Câu hỏi:
   

   Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình $\left(S\right):x^2+y^2+z^2-2x-4y-6z+5=0.$ Tính diện tích mặt cầu (S)

   A. $42\pi$

   B. $12\pi$

   C. $9\pi$

   D. $36\pi$

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   – Dựa vào phương trình mặt cầu xác định bán kính mặt cầu: Mặt cầu $\left(S\right):x^2+y^2+z^2+2ax+2by+2cz+d=0$ có bán kính $R=\sqrt{a^2+b^2+c^2-d}.$
   – Diện tích mặt cầu bán kính R là $S=4\pi R^2.$
   Cách giải:
   Mặt cầu $\left(S\right):x^2+y^2+z^2-2z-4y-6z+5=0$ có bán kính $R=\sqrt{1^2+2^2+3^2-5}=3.$
   Vậy diện tích mặt cầu (S) là $S=4\pi R^2=4\pi .9=36\pi .$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====