Cho hình chóp S.ABC có AB=AC=4, BC=2, SA=43, ∠SAB=∠SAC=300. Gọi G1;G2;G3lần lượt là trọng tâm các tam giác ΔSBC,ΔSCA,ΔSAB và T đối xứng với S qua mặt phẳng (ABC). Thể tích khối chóp TG1G2G3bằng \(\frac{a}{b}\), với a,b∈ℕ và ab tối giản. Tính giá trị của biểu thức P=2a−b.

Câu hỏi:

Cho hình chóp S.ABC có AB=AC=4, BC=2, $SA=4\sqrt{3}$, $\angle SAB=\angle SAC={30}^0$. Gọi $G_1;G_2;G_3$lần lượt là trọng tâm các tam giác $\Delta SBC,\Delta SCA,\Delta SAB$ và T đối xứng với S qua mặt phẳng (ABC). Thể tích khối chóp $T{G}_1{G}_2{G}_3$bằng \(\frac{a}{b}\), với $a,b\in \mathbb{N}$ và $\frac{a}{b}$ tối giản. Tính giá trị của biểu thức $P=2a-b$.

A.3

B.

C.5

Đáp án chính xác

D.1

Trả lời:

Phương pháp giải:
– Gọi M là trung điểm của BC, chứng minh $BC\perp \left(SAM\right)$, từ đó xác định chiều cao hạ từ đỉnh S của khối chóp bằng cách sử dụng định lí: Cho hai mặt phẳng vuông góc, đường thẳng nằm trong mặt này và vuông góc với giao tuyến thì sẽ vuông góc với mặt phẳng kia.
– Xác định tỉ số \(\frac{{d\left( {T;\left( {{G_1}{G_2}{G_3}} \right)} \right)}}{{d\left( {S;\left( {ABC} \right)} \right)}};{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \frac{{{S_{\Delta {G_1}{G_2}{G_3}}}}}{{{S_{\Delta ABC}}}}\), từ đó suy ra tỉ số $\frac{V_{T.G_1{G}_2{G}_3}}{V_{S.ABC}}$.
– Tính chiều cao của khối chóp, chính là chiều cao của tam giác SAM nhờ vào diện tích tam giác SAM, muốn tính$S_{\Delta SAM}$ ta sử dụng định lí Pytago tính từng cạnh của tam giác sau đó áp dụng công thức He-rong $S_{\Delta SAM}=\sqrt{p(p-SA)(p-AM)(p-SM)}$với p là nửa chu vi tam giác SAM.
– Tính $V_{S.ABC}$, từ đó tính $V_{T.G_1{G}_2{G}_3}$, suy ra \(a,{\mkern 1mu} {\mkern 1mu} b\) và tính P.
Giải chi tiết:

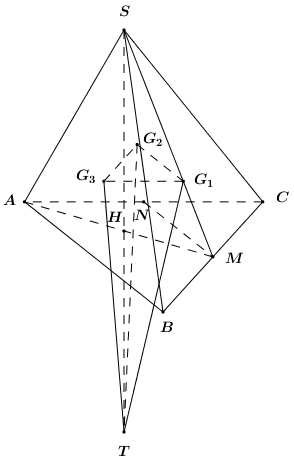
Xét tam giác SAB và $\Delta SAC$có:
SA chung
\(AB = AC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\)
$\angle SAB=\angle SAC={30}^0\left(gt\right)$
$\Rightarrow \Delta SAB=\Delta SAC(c.g.c)$
$\Rightarrow SB=SC$ (2 cạnh tương ứng) $\Rightarrow \Delta SBC$ cân tại S.
Gọi M,N lần lượt là trung điểm của BC,AC ta có
$\{\begin{array}{l}SM\perp BC\\ AM\perp BC\end{array}\Rightarrow BC\perp \left(SAM\right)$.
Trong (SAM) kẻ $SH\perp AM(H\in AM)$ ta có: $\{\begin{array}{l}SH\perp AM\\ SH\perp BC(BC\perp \left(SAM\right))\end{array}\Rightarrow SH\perp \left(ABC\right)$.
Dễ thấy $\left(G_1{G}_2{G}_3\right)//\left(ABC\right)$ và $\frac{d(S;\left(G_1{G}_2{G}_3\right))}{d(S;\left(ABC\right))}=\frac{S{G}_1}{SM}=\frac{2}{3}$
$\Rightarrow d(S;\left(G_1{G}_2{G}_3\right))=\frac{2}{3}SH$.
\( \Rightarrow d\left( {T;\left( {{G_1}{G_2}{G_3}} \right)} \right) = 2SH – \frac{2}{3}SH = \frac{4}{3}SH\).
Lại có $\Delta G_1{G}_2{G}_3$ đồng dạng với $\Delta ABC$ theo tỉ số $k=\frac{G_1{G}_2}{AB}=\frac{G_1{G}_2}{MN}.\frac{MN}{AB}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}$.
$\Rightarrow S_{\Delta G_1{G}_2{G}_3}=\frac{1}{9}{S}_{\Delta ABC}$
$\Rightarrow \frac{V_{T.G_1{G}_2{G}_3}}{V_{S.ABC}}=\frac{d(T;\left(G_1{G}_2{G}_3\right))}{d(S;\left(ABC\right))}.\frac{S_{\Delta G_1{G}_2{G}_3}}{S_{\Delta ABC}}=\frac{4}{3}.\frac{1}{9}=\frac{4}{27}$

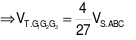
Xét tam giác vuông \(ABM\) có: $AM=\sqrt{A{B}^2-B{M}^2}=\sqrt{4^2-1^2}=\sqrt{15}$.
$\Rightarrow S_{\Delta ABC}=\frac{1}{2}AM.BC=\frac{1}{2}.\sqrt{15}.2=\sqrt{15}$.
Xét tam giác SAB có:
$S{B}^2=S{A}^2+A{B}^2-2SA.AB.\cos \angle SAB$
$={\left(4\sqrt{3}\right)}^2+4^2-2.4\sqrt{3}\mathrm{.4.}\cos {30}^0=16$
\( \Rightarrow SB = 4 = SC\)
Xét tam giác vuông \(SBM\) có $SM=\sqrt{S{B}^2-B{M}^2}=\sqrt{4^2-1^2}=\sqrt{15}$.
Gọi 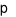là nửa chu vi tam giác SAM ta có $p=\frac{SA+AM+SM}{2}=\frac{4\sqrt{3}+\sqrt{15}+\sqrt{15}}{2}=2\sqrt{3}+\sqrt{15}$.
$\Rightarrow S_{\Delta SAM}=\sqrt{p(p-SA)(p-AM)(p-SM)}=\sqrt{36}=6$.
Lại có $S_{\Delta SAM}=\frac{1}{2}SH.AM\Rightarrow SH=\frac{2S_{\Delta SAM}}{AM}=\frac{2.6}{\sqrt{15}}=\frac{12}{\sqrt{15}}$.
$\Rightarrow V_{S.ABC}=\frac{1}{3}SH.S_{\Delta ABC}=\frac{1}{3}.\frac{12}{\sqrt{15}}.\sqrt{15}=4$.
$\Rightarrow V_{T.G_1{G}_2{G}_3}=\frac{4}{27}{V}_{S.ABC}=\frac{4}{27}.4=\frac{16}{27}$.
$\Rightarrow a=16;b=27$. Vậy $P=2a-b=2.16-27=5$.
Đáp án C.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Thể tích khối cầu có bán kính r là:
   
   

   Câu hỏi:
   

   Thể tích khối cầu có bán kính $r$ là:

   A. $\frac{4}{3}\pi r^3$

   Đáp án chính xác

   B. $\frac{1}{3}\pi r^3$

   C. $\frac{4}{3}\pi r^2$

   D. $4\pi r^3$

   Trả lời:

   Phương pháp giải:
   Thể tích khối cầu có bán kính $r$ là $\frac{4}{3}\pi r^3$.
   Giải chi tiết:
   Thể tích khối cầu có bán kính $r$là $\frac{4}{3}\pi r^3$.
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu u1=1, công bội q=2. Tổng ba số hạng đầu của cấp số nhân là:
   
   

   Câu hỏi:
   

   Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu $u_1=1$, công bội $q=2$. Tổng ba số hạng đầu của cấp số nhân là:

   A. 9

   B. 3

   C. 5

   D. 7

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   Tổng n số hạng đầu tiên của CSN có số hạng đầu $u_1$, công bội q là $S_n=\frac{u_1(1-q^n)}{1-q}$.
   Giải chi tiết:
   Tổng ba số hạng đầu của cấp số nhân có $u_1=1$và $q=2$ là: $S_3=\frac{u_1(1-q^3)}{1-q}=\frac{1.(1-2^3)}{1-2}=7$
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
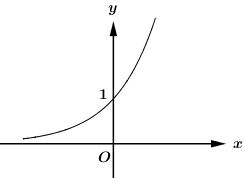
3. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   
   

   Câu hỏi:
   

   Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   

   A.$y={\log }_{3}x$

   B.$y={\log }_{\frac{1}{3}}x$

   C.$y=3^x$

   Đáp án chính xác

   D.$y={\left(\frac{1}{3}\right)}^x$

   Trả lời:

   Phương pháp giải:
   – Hàm số $y={\log }_{a}x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi 0 < a < 1, hàm số nghịch biến trên D.
   – Hàm số $y=a^x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi $0<a<1$, hàm số nghịch biến trên D.
   Giải chi tiết:
   Dựa vào đồ thị ta thấy hàm số đồng biến trên \(\mathbb{R}\) nên chỉ có đáp án C thỏa mãn, tức là hàm số $y=3^x$
   Đáp án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tập nghiệm S của phương trình (20202021)4x=(20212020)2x−6.
   
   

   Câu hỏi:
   

   Tìm tập nghiệm S của phương trình ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$.

   A.$S=\{-3\}$

   B.$S=\left\{3\right\}$

   C.$S=\{-1\}$

   D.$S=\left\{1\right\}$

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   – Sử dụng công thức ${\left(\frac{1}{a}\right)}^m=a^{-m}$.
   – Giải phương trình mũ dạng $a^{f\left(x\right)}=a^{g\left(x\right)}\iff f\left(x\right)=g\left(x\right)$.
   Giải chi tiết:
   Ta có:
   ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$
   $\iff {\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2020}{2021}\right)}^{6-2x}$
   $\iff 4x=6-2x\iff 6x=6\iff x=1$
   Vậy tập nghiệm của phương trình là $S=\left\{1\right\}$.
   Đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=1log3(x2−2x+3m)có tập xác định là \(\mathbb{R}\).
   
   

   Câu hỏi:
   

   Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có tập xác định là \(\mathbb{R}\).

   A.$[\frac{2}{3};10]$

   B.$(\frac{2}{3};+\infty )$

   Đáp án chính xác

   C.$[\frac{2}{3};+\infty )$

   D.$(-\infty ;\frac{2}{3})$

   Trả lời:

   Phương pháp giải:
   – Hàm căn thức xác định khi biểu thức trong căn không âm.
   – Hàm $y={\log }_{a}f\left(x\right)$xác định khi và chỉ khi $f\left(x\right)$ xác định và $f\left(x\right)>0$.
   Giải chi tiết:
   Hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có TXĐ là \(\mathbb{R}\) khi và chỉ khi:
   $\{\begin{array}{l}{\log }_3(x^2-2x+3m)>0\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}\iff \{\begin{array}{l}{x}^2-2x+3m>1\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}$
   $\iff x^2-2x+3m>1\forall x\in ℝ\iff x^2-2x-1>-3m\forall x\in ℝ(*)$
   Đặt $f\left(x\right)=x^2-2x-1$ ta có $f^{‘}\left(x\right)=2x-2=0\iff x=1$.
   BBT:
   
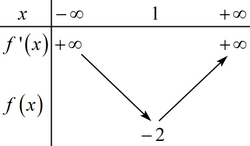
   Dựa vào BBT và từ (*) ta có $f\left(x\right)>-3m\forall x\in ℝ$$\iff -3m<\underset{ℝ}{min}f\left(x\right)=-2\iff m>\frac{2}{3}$.
   Vậy $m\in (\frac{2}{3};+\infty )$.
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====