Cho hàm số y=f(x) có đạo hàm trên R. Mệnh đề nào dưới đây là đúng?

Câu hỏi:

Cho hàm số y=f(x) có đạo hàm trên R. Mệnh đề nào dưới đây là đúng?

A. Nếu hàm số đạt cực trị tại $x_0$ thì đạo hàm đổi dấu khi x qua $x_0$.

Đáp án chính xác

B. Nếu đạo hàm đổi dấu khi x qua $x_0$ thì hàm số đạt cực tiểu tại $x_0$.

C. Nếu \(f’\left( {{x_0}} \right) = 0\) thì hàm số đạt cực trị tại $x_0$.

D. Nếu $f^{‘}\left(x_0\right)=f^{”}\left(x_0\right)=0$ thì hàm số không đạt cực trị tại $x_0$.

Trả lời:

Phương pháp giải:
Sử dụng lý thuyết về Cực trị của hàm số:
Ta có: $x=x_0$ là điểm cực trị của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm $x=x_0$ thì hàm số có y’ đổi dấu từ dương sang âm hoặc ngược lại.
Điểm $x=x_0$ là điểm cực tiểu của hàm số $y=f\left(x\right)\iff$tại điểm $x=x_0$ thì hàm số có y’ đổi dấu từ âm sang dương.
Điểm $x=x_0$ là điểm cực đại của hàm số $y=f\left(x\right)\iff$tại điểm $x=x_0$ thì hàm số có y’ đổi dấu từ dương sang âm.
Ta có: $x=x_0$là điểm cực trị của hàm số $y=f\left(x\right)\Rightarrow f^{‘}\left(x_0\right)=0.$
Điểm $x=x_0$là điểm cực đại của hàm số $y=f\left(x\right)\iff \{\begin{array}{l}{f}^{‘}\left(x_0\right)=0\\ f^{”}\left(x_0\right)<0\end{array}.$
Điểm $x=x_0$là điểm cực tiểu của hàm số $y=f\left(x\right)\iff \{\begin{array}{l}{f}^{‘}\left(x_0\right)=0\\ f^{”}\left(x_0\right)>0\end{array}.$
Giải chi tiết:
Ta có: $x=x_0$ là điểm cực trị của hàm số $y=f\left(x\right)\iff$ tại điểm $x=x_0$ thì hàm số có y’ đổi dấu từ dương sang âm hoặc ngược lại.
⇒ Đáp án A đúng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Thể tích khối cầu có bán kính r là:
   
   

   Câu hỏi:
   

   Thể tích khối cầu có bán kính $r$ là:

   A. $\frac{4}{3}\pi r^3$

   Đáp án chính xác

   B. $\frac{1}{3}\pi r^3$

   C. $\frac{4}{3}\pi r^2$

   D. $4\pi r^3$

   Trả lời:

   Phương pháp giải:
   Thể tích khối cầu có bán kính $r$ là $\frac{4}{3}\pi r^3$.
   Giải chi tiết:
   Thể tích khối cầu có bán kính $r$là $\frac{4}{3}\pi r^3$.
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu u1=1, công bội q=2. Tổng ba số hạng đầu của cấp số nhân là:
   
   

   Câu hỏi:
   

   Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu $u_1=1$, công bội $q=2$. Tổng ba số hạng đầu của cấp số nhân là:

   A. 9

   B. 3

   C. 5

   D. 7

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   Tổng n số hạng đầu tiên của CSN có số hạng đầu $u_1$, công bội q là $S_n=\frac{u_1(1-q^n)}{1-q}$.
   Giải chi tiết:
   Tổng ba số hạng đầu của cấp số nhân có $u_1=1$và $q=2$ là: $S_3=\frac{u_1(1-q^3)}{1-q}=\frac{1.(1-2^3)}{1-2}=7$
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   
   

   Câu hỏi:
   

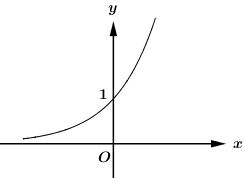
   Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   

   A.$y={\log }_{3}x$

   B.$y={\log }_{\frac{1}{3}}x$

   C.$y=3^x$

   Đáp án chính xác

   D.$y={\left(\frac{1}{3}\right)}^x$

   Trả lời:

   Phương pháp giải:
   – Hàm số $y={\log }_{a}x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi 0 < a < 1, hàm số nghịch biến trên D.
   – Hàm số $y=a^x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi $0<a<1$, hàm số nghịch biến trên D.
   Giải chi tiết:
   Dựa vào đồ thị ta thấy hàm số đồng biến trên \(\mathbb{R}\) nên chỉ có đáp án C thỏa mãn, tức là hàm số $y=3^x$
   Đáp án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tập nghiệm S của phương trình (20202021)4x=(20212020)2x−6.
   
   

   Câu hỏi:
   

   Tìm tập nghiệm S của phương trình ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$.

   A.$S=\{-3\}$

   B.$S=\left\{3\right\}$

   C.$S=\{-1\}$

   D.$S=\left\{1\right\}$

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   – Sử dụng công thức ${\left(\frac{1}{a}\right)}^m=a^{-m}$.
   – Giải phương trình mũ dạng $a^{f\left(x\right)}=a^{g\left(x\right)}\iff f\left(x\right)=g\left(x\right)$.
   Giải chi tiết:
   Ta có:
   ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$
   $\iff {\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2020}{2021}\right)}^{6-2x}$
   $\iff 4x=6-2x\iff 6x=6\iff x=1$
   Vậy tập nghiệm của phương trình là $S=\left\{1\right\}$.
   Đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=1log3(x2−2x+3m)có tập xác định là \(\mathbb{R}\).
   
   

   Câu hỏi:
   

   Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có tập xác định là \(\mathbb{R}\).

   A.$[\frac{2}{3};10]$

   B.$(\frac{2}{3};+\infty )$

   Đáp án chính xác

   C.$[\frac{2}{3};+\infty )$

   D.$(-\infty ;\frac{2}{3})$

   Trả lời:

   Phương pháp giải:
   – Hàm căn thức xác định khi biểu thức trong căn không âm.
   – Hàm $y={\log }_{a}f\left(x\right)$xác định khi và chỉ khi $f\left(x\right)$ xác định và $f\left(x\right)>0$.
   Giải chi tiết:
   Hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có TXĐ là \(\mathbb{R}\) khi và chỉ khi:
   $\{\begin{array}{l}{\log }_3(x^2-2x+3m)>0\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}\iff \{\begin{array}{l}{x}^2-2x+3m>1\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}$
   $\iff x^2-2x+3m>1\forall x\in ℝ\iff x^2-2x-1>-3m\forall x\in ℝ(*)$
   Đặt $f\left(x\right)=x^2-2x-1$ ta có $f^{‘}\left(x\right)=2x-2=0\iff x=1$.
   BBT:
   
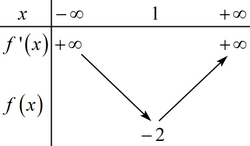
   Dựa vào BBT và từ (*) ta có $f\left(x\right)>-3m\forall x\in ℝ$$\iff -3m<\underset{ℝ}{min}f\left(x\right)=-2\iff m>\frac{2}{3}$.
   Vậy $m\in (\frac{2}{3};+\infty )$.
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====