Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. SA=SB=a,  SC=SD=a3. Gọi E, G lần lượt là trung điểm của SA và SB. M là điểm tùy ý trên cạnh BC (không trùng với B, C). a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD) và (SBC)

Câu hỏi:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. $SA=SB=a,SC=SD=a\sqrt{3}$. Gọi E, G lần lượt là trung điểm của SA và SB. M là điểm tùy ý trên cạnh BC (không trùng với B, C).
a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD) và (SBC)

Trả lời:

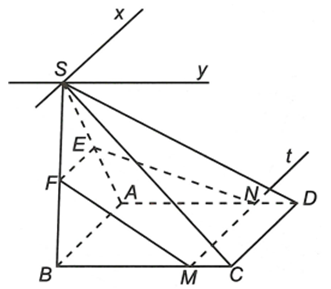
a) Ta có 
$\left\{\begin{array}{l}S\in \left(SAD\right)\cap \left(SCD\right)\\ AB/\text{}/CD,AB\subset \left(SAB\right),CD\subset \left(SCD\right)\end{array}\right.$
$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=Sx$, trong đó Sx // AB // CD
Tương tự $\left\{\begin{array}{l}S\in \left(SAD\right)\cap \left(SBC\right)\\ AD/\text{}/BC,AD\subset \left(SAD\right),BC\subset \left(SBC\right)\end{array}\right.$
$\Rightarrow \left(SAD\right)\cap \left(SBC\right)=Sy$, trong đó Sy // AD // BC.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). Chứng minh PQ // MN và PQ // AC
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). Chứng minh PQ // MN và PQ // AC

   Trả lời:

   

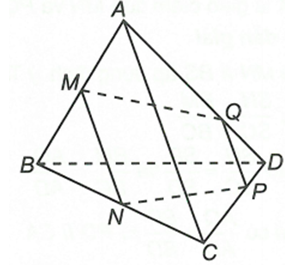
   Ta có $CD\cap \left(MNP\right)=\left\{P\right\}$ và MN // AC
   Suy ra $\left(MNP\right)\cap \left(ACD\right)=Px$
   Trong đó Px // MN // AC
   Mặt khác $DA\cap \left(MNP\right)=\left\{Q\right\}$ nên $Q\in Px$
   Vậy PQ // MN // AC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD AB>CD. Gọi M, N lần lượt là trung điểm của SA, SB. a) Chứng minh MN // CD
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD $\left(AB>CD\right)$. Gọi M, N lần lượt là trung điểm của SA, SB.
   a) Chứng minh MN // CD

   Trả lời:

   

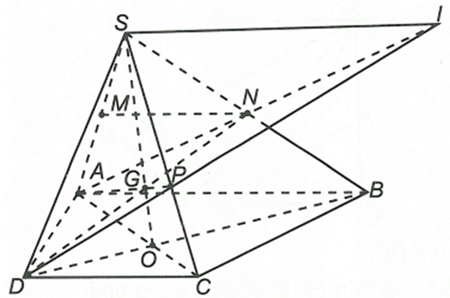
   a) Ta có MN là đường trung bình của tam giác SAB suy ra MN // AB. Mà AB // CD nên MN // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I. Chứng minh SI // AB // CD
   
   

   Câu hỏi:
   

   b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I.
   Chứng minh SI // AB // CD

   Trả lời:

   b) Gọi $\left\{O\right\}=AC\cap BD,\left\{G\right\}=SO\cap DN$ và $\left\{P\right\}=AG\cap SC$
   suy ra $\left\{P\right\}=SC\cap \left(ADN\right)$
   Ta có AB // CD nên $\left(SAB\right)\cap \left(SCD\right)=Sx$ sao cho Sx // AB // CD
   Theo đầu bài $\left\{I\right\}=AN\cap DP$ nên $I\in \left(SAB\right)$và $I\in \left(SCD\right)\Rightarrow I\in Sx$
   Từ đó ta có SI // AB // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD a) Chứng minh PQ // SA
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD
   a) Chứng minh PQ // SA

   Trả lời:

   

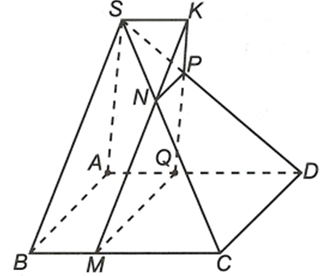
   a) Ta có MN // BS áp dụng định lý Ta-lét ta được $\frac{SN}{SC}=\frac{BM}{BC}$
   Tương tự $\frac{SN}{SC}=\frac{SP}{SD}$và $\frac{BM}{BC}=\frac{AQ}{AD}$
   Từ đó ta có $\frac{AQ}{AD}=\frac{SP}{SD}\Rightarrow PQ/\text{}/SA$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) Gọi K là giao điểm của MN và PQ. Chứng minh SK // SD // BC
   
   

   Câu hỏi:
   

   b) Gọi K là giao điểm của MN và PQ. Chứng minh SK // SD // BC

   Trả lời:

   b) Do AD // BC nên $\left(SAD\right)\cap \left(SBC\right)=Sx$ trong đó Sx // AD // BC
   Mặt khác $\left\{K\right\}=MN\cap QP$ nên K là điểm chung của hai mặt phẳng (SAD) và (SBC) suy ra $K\in Sx$
   Vậy Sx // AD // BC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====