Tìm m để tam thức f(x) = – x2 – 2x + m – 12 không dương với mọi x ∈ ℝ.

Câu hỏi:

Tìm m để tam thức f(x) = – x² – 2x + m – 12 không dương với mọi x ∈ ℝ.

Trả lời:

Lời giải
Tam thức f(x) = – x² – 2x + m – 12 không dương với mọi x ∈ ℝ nghĩa là f(x) ≤ 0 với mọi x ∈ ℝ.
Xét tam thức f(x) = – x² – 2x + m – 12, có a = – 1 < 0 và ∆ = (– 2)² – 4.(– 1)(m – 12) = 4m – 44.
Vì a = – 1 < 0 nên để f(x) ≤ 0 với mọi x ∈ ℝ ⇔ ∆ ≤ 0
⇔ 4m – 44 ≤ 0
⇔ 4m ≤ 44
⇔ m ≤ 11
Vậy với m ≤ 11 thì tam thức f(x) = – x² – 2x + m – 12 không dương với mọi x ∈ ℝ.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các phát biểu sau, phát biểu nào sai? A. x2 – x – 2 > 0 khi và chỉ khi x ∈ (– ∞ ; –1)∪(2 ; +∞). B. x2 – x – 2 ≤ 0 khi và chỉ khi x ∈ [–1 ; 2]. C. x2 – x – 2 < 0 khi và chỉ khi x ∈ (–1 ; 2). D. x2 – x – 2 ≥ 0 khi và chỉ khi x ∈ (– ∞; –1)∪(2; +∞).
   
   

   Câu hỏi:
   

   Trong các phát biểu sau, phát biểu nào sai?
   A. x² – x – 2 > 0 khi và chỉ khi x ∈ (– ∞ ; –1)∪(2 ; +∞).
   B. x² – x – 2 ≤ 0 khi và chỉ khi x ∈ [–1 ; 2].
   C. x² – x – 2 < 0 khi và chỉ khi x ∈ (–1 ; 2).
   D. x² – x – 2 ≥ 0 khi và chỉ khi x ∈ (– ∞; –1)∪(2; +∞).

   Trả lời:

   Lời giải
   Đáp án đúng là D
   Xét biểu thức f(x) x² – x – 2 là tam thức bậc hai, có a = 1 > 0 và (– 1)² – 4.1.(– 2) = 9 > 0.
   Do đó tam thức có hai nghiệm phân biệt x₁ = – 1 và x₂ = 2.
   Theo định lí về dấu tam thức bậc hai ta có:
   f(x) > 0 khi x ∈ (– ∞ ; –1)∪(2 ; +∞);
   f(x) < 0 khi x ∈ (–1 ; 2);
   f(x) = 0 khi x = – 1 hoặc x = 2.
   Do đó A, B, C đúng còn D sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y = f(x) có đồ thị ở Hình 15. Trong các phát biểu sau, phát biểu nào sai? A. f(x) < 0 khi và chỉ khi x ∈ (1 ; 3). B. f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1]∪[3; +∞). C. f(x) > 0 khi và chỉ khi x ∈ (1 ; 3). D. f(x) ≥ 0 khi và chỉ khi x ∈ [1 ; 3].
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) có đồ thị ở Hình 15.
   
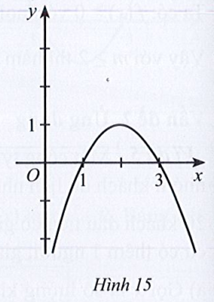
   Trong các phát biểu sau, phát biểu nào sai?
   A. f(x) < 0 khi và chỉ khi x ∈ (1 ; 3).
   B. f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1]∪[3; +∞).
   C. f(x) > 0 khi và chỉ khi x ∈ (1 ; 3).
   D. f(x) ≥ 0 khi và chỉ khi x ∈ [1 ; 3].

   Trả lời:

   Lời giải
   Đáp án đúng là A
   Dựa vào đồ thị hàm số ta nhận thấy:
   Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ lần lượt là x = 1 và x = 3. Suy ra f(x) = 0 tại x = 1 hoặc x = 3.
   Đồ thị hàm số nằm phía trên trục hoành khi x ∈ (1; 3). Suy ra f(x) > 0 khi x ∈ (1; 3).
   Đồ thị hàm số nằm phía dưới trục hoành khi x ∈ (– ∞; 1) ∪ (3; +∞). Suy ra f(x) < 0 khi x ∈ (– ∞; 1) ∪ (3; +∞).
   Vậy đáp án A sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0). Trong các phát biểu sau, phát biểu nào đúng? A. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0. B. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ < 0. C. f(x) ≤ 0 với mọi x khi và chỉ khi a > 0 và ∆ < 0. D. f(x) ≤ 0 với mọi x khi và chỉ khi a > 0 và ∆ ≤ 0.
   
   

   Câu hỏi:
   

   Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Trong các phát biểu sau, phát biểu nào đúng?
   A. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0.
   B. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ < 0.
   C. f(x) ≤ 0 với mọi x khi và chỉ khi a > 0 và ∆ < 0.
   D. f(x) ≤ 0 với mọi x khi và chỉ khi a > 0 và ∆ ≤ 0.

   Trả lời:

   Lời giải
   Đáp án đúng là B
   Theo định lí dấu của tam thức bậc hai ta có:
   Tam thức bậc hai f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ < 0.
   Tam thức bậc hai f(x) ≤ 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0.
   Tam thức bậc hai f(x) > 0 với mọi x khi và chỉ khi a > 0 và ∆ < 0.
   Tam thức bậc hai f(x) ≥ 0 với mọi x khi và chỉ khi a > 0 và ∆ ≤ 0.
   Vậy đáp án đúng là B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Lập bảng xét dấu với mỗi tam thức bậc hai sau: f(x) = 3×2 – 7x + 4;
   
   

   Câu hỏi:
   

   Lập bảng xét dấu với mỗi tam thức bậc hai sau:
   f(x) = 3x² – 7x + 4;

   Trả lời:

   Lời giải
   Xét tam thức bậc hai f(x) = 3x² – 7x + 4 , có a = 3 > 0 và ∆ = (– 7)² – 4.3.4 = 1 > 0.
   Suy ra tam thức có hai nghiệm phân biệt x = 1 và x = \(\frac{4}{3}\).
   Khi đó ta có bảng xét dấu sau:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. f(x) = 25×2 + 10x + 1;
   
   

   Câu hỏi:
   

   f(x) = 25x² + 10x + 1;

   Trả lời:

   Lời giải
   Xét tam thức bậc hai f(x) = 25x² + 10x + 1, có a = 25 > 0 và ∆ = 10² – 4.25.1 = 0.
   Suy ra tam thức có nghiệm kép x = \( – \frac{1}{5}\).
   Khi đó ta có bảng xét dấu sau:
   

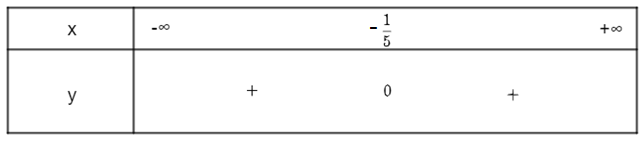
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====