Số phần tử của tập hợp A = {x  ∈ N : x là số nguyên tố nhỏ hơn 20} là:

Câu hỏi:

Số phần tử của tập hợp A = {x  ∈ N : x là số nguyên tố nhỏ hơn 20} là:

A. 8.

Đáp án chính xác

B. 9

C. 7

D. 10

Trả lời:

Đáp án: AA = {2; 3; 5; 7; 11; 13; 17; 19}  => có 8 phần tử.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Mệnh đề “∃x ∈ R : x2 = 5” khẳng định rằng
   
   

   Câu hỏi:
   

   Mệnh đề “∃x ∈ R : x² = 5” khẳng định rằng

   A. Bình phương của mỗi số thực bằng 5

   B. Có ít nhất một số thực mà bình phương của nó bằng 5

   Đáp án chính xác

   C. Chỉ có một số thực bình phương bằng 5

   D. Nếu x là số thực thì x² = 5

   Trả lời:

   Đáp án: BA sai, chẳng hạn bình phương của số thực 3 là 9 khác 5.C sai, có 2 số thực là 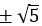bình phương bằng 5.D sai, chẳng hạn nếu x = 2 là số thực thì  x²   ≠ 5

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Với giá trị nào của n thì mệnh đề chứa biến “ n chia hết cho 9” là đúng?
   
   

   Câu hỏi:
   

   Với giá trị nào của n thì mệnh đề chứa biến “ n chia hết cho 9” là đúng?

   A. 24

   B. 15

   C. 18

   Đáp án chính xác

   D. 30

   Trả lời:

   Đáp án: Cn = 18 chia hết cho 9. Các giá trị n khác không chia hết cho 9.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Phủ định của mệnh đề “ ∀x ∈ R ,  x2 – x – 6 < 0” là:
   
   

   Câu hỏi:
   

   Phủ định của mệnh đề “ ∀x ∈ R ,  x² – x – 6 < 0” là:

    A. ∃x ∈ R ,  x² – x – 6 > 0

   B. ∀x ∈ R ,  x² – x – 6 > 0

   C. ∃x ∉ R ,  x² – x – 6 ≥ 0

   D. ∃x ∈ R ,  x² – x – 6 ≥ 0

   Đáp án chính xác

   Trả lời:

   Đáp án: DPhủ  định của  ∀x ∈ R   là  ∃x ∈ R . Phủ định của  x² – x – 6 < 0 là  x² – x – 6 ≥ 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Phủ định của mệnh đề “ ∃x∈ R, x2 + 2x + 5 là số nguyên tố” là
   
   

   Câu hỏi:
   

   Phủ định của mệnh đề “ ∃x∈ R, x² + 2x + 5 là số nguyên tố” là

    A. ∀x ∈ R , x² + 2x + 5  là hợp số

   Đáp án chính xác

   B. ∃x ∈ R , x² + 2x + 5  là hợp số

   C. ∀x ∉ R , x² + 2x + 5  là hợp số

   D. ∃x ∈ R , x² + 2x + 5  là số thực

   Trả lời:

   Đáp án: APhủ  định của  ∃x ∈ R  là  ∀x ∈ R . Phủ định của x² + 2x + 5 là số nguyên tố là x² + 2x + 5 là hợp số.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Phủ định của mệnh đề “ ∃x ∈ R , x – 3  ≥ 0” là
   
   

   Câu hỏi:
   

   Phủ định của mệnh đề “ ∃x ∈ R , x – 3  ≥ 0” là

   A.  ∀x ∈ R, x – 3  ≥ 0

   B.  ∃x ∈ R, x – 3  < 0

   C.  ∀x ∈ R, x – 3  < 0

   Đáp án chính xác

   D.  ∃x ∈ R, x – 3  > 0

   Trả lời:

   Đáp án: CPhủ  định của  ∃x  ∈ R  là  ∀x  ∈ R . Phủ định của x – 3  ≥ 0 là x – 3  < 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====