Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau: – Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B. – Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B. Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn 12 số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất là:

Câu hỏi:

Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:
– Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.
– Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B.
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn $\frac{1}{2}$ số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A.
Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất là:

A. 500 đơn vị vitamin A và 500 đơn vị vitamin B;

B. 600 đơn vị vitamin A và 400 đơn vị vitamin B;

C. 600 đơn vị vitamin A và 300 đơn vị vitamin B;

D. 100 đơn vị vitamin A và 300 đơn vị vitamin B.

Đáp án chính xác

Trả lời:

Hướng dẫn giải
Đáp án đúng là: D
Gọi x là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày. (x ≥ 0)
Gọi y là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày. (y ≥ 0)
Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên x ≤ 600 và y ≤ 500.
Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B nên:
400 ≤ x + y ≤ 1000.
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn $\frac{1}{2}$ số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A nên:
$\left\{\begin{array}{l}y\ge \frac{1}{2}x\\ y\le 3x\end{array}\right.$.

Ta có hệ bất phương trình giữa x và y:
 $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x\le 600\\ y\le 500\\ x+y\ge 400\\ x+y\le 1000\\ y\ge \frac{1}{2}x\\ y\le 3x\end{array}\right.$
Biểu diễn miền nghiệm của hệ bất phương trình:
– Biểu diễn miền nghiệm D₁ của bất phương trình x ≤ 600:
+ Vẽ đường thẳng d₁: x = 600 trên mặt phẳng tọa độ Oxy.
+ Thay x = 0, y = 0 vào bất phương trình ta được 0 ≤ 600 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x ≤ 600.
Vậy miền nghiệm D₁ của bất phương trình x ≤ 600 là nửa mặt phẳng bờ d₁ (kể cả bờ d₁) chứa điểm O.
* Tương tự ta biểu diễn các miền nghiệm:
– Miền nghiệm D₂ của bất phương trình y ≤ 500: là nửa mặt phẳng bờ d₂ (kể cả bờ d₂: y = 500) chứa điểm O.
– Miền nghiệm D₃ của bất phương trình x + y ≥ 400: là nửa mặt phẳng bờ d₃ (kể cả bờ d₃: x + y = 400) không chứa điểm O.
– Miền nghiệm D₄ của bất phương trình x + y ≤ 1000: là nửa mặt phẳng bờ d₄ (kể cả bờ d₄: x + y = 1000) chứa điểm O.
– Miền nghiệm D₅ của bất phương trình y ≥ $\frac{1}{2}$ x: là nửa mặt phẳng bờ d₅ (kể cả bờ d₅: $y=\frac{1}{2}x$ ) chứa điểm M(0; 50).
– Miền nghiệm D₆ của bất phương trình y ≤ 3x: là nửa mặt phẳng bờ d₆ (kể cả bờ d₆: y = 3x) không chứa điểm M (0; 50).
Ta có đồ thị sau:

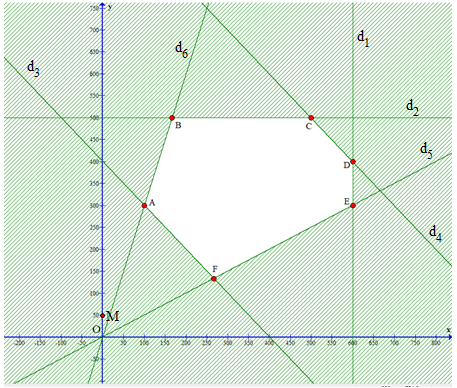
Miền nghiệm của hệ bất phương trình là miền của đa giác ABCDEF với:
A(100; 300), B $\left(\frac{500}{3};500\right)$, C(500; 500), D(600, 400), E(600, 300), F $\left(\frac{800}{3};\frac{400}{3}\right)$
Số tiền trả cho x đơn vị vitamin A và y đơn vị vitamin B là: F (x; y) = 9x + 7,5y.
Để có số tiền phải trả là ít nhất thì F(x; y) phải nhỏ nhất.
Tại A(100; 300): F = 9.100 + 7,5. 300 = 3150;
Tại B $\left(\frac{500}{3};500\right)$: F = 9.$\frac{500}{3}$  + 7,5. 500 = 5250;
Tại C(500; 500): F = 9. 500 + 7,5. 500 = 8250;
Tại D(600, 400): F = 9. 600 + 7,5. 400 = 8400;
Tại E(600, 300): F = 9. 600 + 7,5. 300 = 7650;
Tại F $\left(\frac{800}{3};\frac{400}{3}\right)$: F = 9. $\frac{800}{3}$+ 7,5. $\frac{400}{3}$  = 3400;
Vậy F(x; y) nhỏ nhất là 3150 khi x =100 và y = 300.
Vậy mỗi người sẽ dùng 100 đơn vị vitamin A và 300 đơn vị vitamin B để đảm bảo các điều kiện số lượng sử dụng và chi phí phải trả là ít nhất.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các bất phương trình sau đây, đâu là bất phương trình bậc nhất hai ẩn?
   
   

   Câu hỏi:
   

   Trong các bất phương trình sau đây, đâu là bất phương trình bậc nhất hai ẩn?

   A. 3x + 4y – z + 1 > 0;

   B. 2x – 2y – 1 > 0;

   Đáp án chính xác

   C. x² + y < 3;

   D. $\frac{3x}{4y}$  – x > 0.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Câu A: 3x + 4y – z + 1 > 0 là bất phương trình bậc nhất 3 ẩn x, y, z nên không là bất phương trình bậc nhất hai ẩn.
   Câu B: 2x – 2y – 1 > 0 là bất phương trình bậc nhất hai ẩn có dạng ax + by + c > 0, a = 2, b = -2, c = -1.
   Câu C: x² + y < 3 là bất phương trình có chứa x² nên không là bất phương trình bậc nhất hai ẩn.
   Câu D: $\frac{3x}{4y}$  – x > 0 không là bất phương trình bậc nhất hai ẩn vì không có dạng ax + by + c > 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
   
   

   Câu hỏi:
   

   Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

   A. $\left\{\begin{array}{l}x+1>0\\ y-1>x\end{array}\right.$

   Đáp án chính xác

   B. $\left\{\begin{array}{l}{x}^2+y^2<0\\ y-x>0\end{array}\right.$

   C. 3y – 2x < 0

   D. $\left\{\begin{array}{l}2x-y^2<5\\ 2x+3y>10\end{array}\right.$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   – Hệ bất phương trình $\left\{\begin{array}{l}x+1>0\\ y-1>x\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn vì có hai bất phương trình x +1 > 0 và y – 1 > x đều là bất phương trình bậc nhất hai ẩn.
   – Hệ bất phương trình $\left\{\begin{array}{l}{x}^2+y^2<0\\ y-x>0\end{array}\right.$ không là hệ bất phương trình bậc nhất hai ẩn vì có bất phương trình x² + y² < 0 không là bất phương trình bậc nhất hai ẩn.
   – Bất phương trình 3y – 2x < 0 không là hệ bất phương trình bậc nhất hai ẩn vì chỉ có một bất phương trình bậc nhất hai ẩn.
   – Hệ bất phương trình không $\left\{\begin{array}{l}2x-y^2<5\\ 2x+3y>10\end{array}\right.$là hệ bất phương trình bậc nhất hai ẩn vì bất phương trình 2x – y² < 5 có chứa y² nên không là bất phương trình bậc nhất hai ẩn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Miền nghiệm của hệ bất phương trình  không chứa điểm nào sau đây?
   
   

   Câu hỏi:
   

   Miền nghiệm của hệ bất phương trình  không chứa điểm nào sau đây?

   A. (1; 1);

   Đáp án chính xác

   B. (10; 3);

   C. (3; 4);

   D. (5; 1).

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Câu A: Thay x = 1 và y = 1 vào bất phương trình x + 2y > 3 ta có: 1 + 2.1 = 3 > 3 là mệnh đề sai nên cặp số (x; y) = (1; 1) không là nghiệm của bất phương trình x + 2y > 3.
   Vậy cặp (x; y) = (1; 1) không là nghiệm của hệ bất phương trình đã cho. Do đó A là đúng.
   Câu B: Thay x = 10 và y = 3 vào bất phương trình x + 2y > 3 ta có: 10 + 2. 3 = 16 > 3 là mệnh đề đúng nên cặp số (x; y) = (10; 3) là nghiệm của bất phương trình x + 2y > 3.
   Thay x = 10 và y = 3 vào bất phương trình x – 2y < 5 ta có: 10 – 2. 3 = 4 < 5 là mệnh đề đúng nên cặp số (x; y) = (10; 3) là nghiệm của bất phương trình x – 2y < 5.
   Cặp (x; y) = (10; 3) là nghiệm của bất phương trình x + 2y > 3 và cũng là nghiệm của bất phương trình x – 2y < 5. Nên cặp (x; y) = (10; 3) là nghiệm của hệ bất phương trình đã cho. Do đó B là sai.
   Tương tự câu A, ta chứng minh được cặp nghiệm (3; 4), (5; 1) là nghiệm của hệ bất phương trình đã cho. Do dó C và D là sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cặp số nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: 2x + y – 1 < 0?
   
   

   Câu hỏi:
   

   Cặp số nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: 2x + y – 1 < 0?

   A. (x; y) = (2; 3);

   B. (x; y) = (1; 2);

   C. (x; y) = (0; 1);

   D. (x; y) = (-1; 0).

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Thay x = 2, y = 3 vào bất phương trình 2x + y – 1 < 0 ta có: 2.2 + 3 – 1 = 6 < 0 là mệnh đề sai, nên (2; 3) không là nghiệm của bất phương trình đã cho.
   Thay x = 1, y = 2 vào bất phương trình 2x + y – 1 < 0 ta có: 2. 1 + 2 – 1 = 3 < 0 là mệnh đề sai, nên (1; 2) không là nghiệm của bất phương trình đã cho.
   Thay x = 0, y = 1 vào bất phương trình 2x + y – 1 < 0 ta có: 2. 0 + 1 – 1 = 0 < 0 là mệnh đề sai, nên (0; 1) không là nghiệm của bất phương trình đã cho.
   Thay x = -1, y = 0 vào bất phương trình 2x + y – 1 < 0 ta có: 2. (-1) + 0 – 1 = -3 < 0 là mệnh đề đúng, nên (-1; 0) là nghiệm của bất phương trình đã cho.
   Vậy ta chọn phương án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hệ bất phương trình x+5y>12x−4y
   
   

   Câu hỏi:
   

   Cho hệ bất phương trình $\left\{\begin{array}{l}x+5y>1\\ 2x-4y<10\end{array}\right.$. Hỏi khi cho y = 0, x có thể nhận mấy giá trị nguyên?

   A. 0

   B. 1

   C. 2

   D. 3

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Hệ bất phương trình $\left\{\begin{array}{l}x+5y>1\\ 2x-4y<10\end{array}\right.$  là hệ bất phương trình bậc nhất hai ẩn.
   Khi y = 0, hệ trở thành:$\left\{\begin{array}{l}x>1\\ 2x<10\end{array}\right.$ ⇔ 1 < x < 5.
   Mà x là số nguyên nên x có thể có các giá trị là {2; 3; 4}
   Vậy có 3 giá trị nguyên nào của x thoả mãn hệ khi y = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====