Lý thuyết Chương 4 (Kết nối tri thức 2023) hay, chi tiết | Toán lớp 7

Lý thuyết Toán lớp 7 Chương 4

A. Lý thuyết Chương 4: Tam giác bằng nhau

1. Tổng các góc trong một tam giác

• Tổng ba góc trong một tam giác bằng 180°.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

• Phân loại tam giác dựa vào số đo góc:

+ Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

+ Tam giác có một góc tù được gọi là tam giác tù.

+ Tam giác có một góc vuông được gọi là tam giác vuông.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

2. Hai tam giác bằng nhau

• Hai tam giác bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

3. Các trường hợp bằng nhau của hai tam giác

• Trường hợp bằng nhau thứ nhất: cạnh – cạnh – cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

4. Các trường hợp bằng nhau của hai tam giác vuông

• Trường hợp: hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh góc vuông – góc nhọn kề

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

5. Tam giác cân

• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

• Tính chất:

+ Trong tam giác cân, hai góc ở đáy bằng nhau.

+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.

• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.

+ Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.

+ Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.

6. Đường trung trực của một đoạn thẳng

• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Tính số đo x, y trong các hình dưới đây:

Hướng dẫn giải

a) Ta có: x + x + 30° + x + 15° = 180° (tổng ba góc trong tam giác)

⇒ 3x + 45° = 180°

⇒ 3x = 180° − 45°

⇒ 3x = 135°

⇒ x = 45°

Vậy x = 45°

b) Ta có: 3y – 10° = y + 60° (góc ngoài của tam giác)

⇒ 2y = 70°

⇒ y = 35°

Có: x + y + 60° = 180° (tổng ba góc trong tam giác)

⇒ x + 35° + 60° = 180°

⇒ x = 85°

Vậy x = 85°; y = 35°

Bài 2. Cho hình dưới đây, biết tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE. Chứng minh rằng:

a) <$\Delta ABD=\Delta EBD$ và $\widehat{BED}=90°$>;

b) BD là đường trung trực của cạnh AE;

c) Tam giác BFC là tam giác cân.

Hướng dẫn giải

a) Xét tam giác ABD và tam giác EBD có:

BA = BE (theo giả thiết)

$\widehat{ABD}=\widehat{EBD}$ (BD là tia phân giác của $\widehat{ABC}$)

BD là cạnh chung

Do đó, $\Delta ABD=\Delta EBD$ (c.g.c)

⇒ $\widehat{BAD}=\widehat{BED}$ (hai góc tương ứng)

Mà $\widehat{BAD}=90°$(theo giả thiết) ⇒ $\widehat{BED}=90°$ (đpcm)

b) Vì $\Delta ABD=\Delta EBD$ (chứng minh trên)

⇒ DA = DE (2 cạnh tương ứng)

⇒ D thuộc đường trung trực của AE (tính chất đường trung trực) (1)

Mà BA = BE (theo giả thiết)

⇒ B thuộc đường trung trực của AE (tính chất đường trung trực) (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE (đpcm)

c) Vì $\widehat{BED}=90°$ (chứng minh trên) ⇒ $\Delta EBF$ vuông tại E

Xét tam giác ABC (vuông tại A) và tam giác EBF (vuông tại E) có:

BA = BE (theo giả thiết)

$\widehat{ABC}$ là góc chung

⇒ $\Delta ABC=\Delta EBF$ (cạnh góc vuông – góc nhọn kề)

⇒ BC = BF (2 cạnh tương ứng)

⇒ $\Delta BFC$ cân tại B (đpcm).

Bài 3. Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Chứng minh rằng:

a) $\Delta AMO=\Delta BNO$;

b) Tam giác AMN cân;

c) Nếu $\widehat{AMO}=30°$ thì tam giác AMB là tam giác đều.

Hướng dẫn giải

MN là đường trung trực của AB ⇒ MN ⊥ AB tại O và OA = OB

a) Xét hai tam giác vuông AMO và BNO có:

AM = BN (theo giả thiết)

OA = OB

⇒ $\Delta AMO=\Delta BNO$ (cạnh huyền – cạnh góc vuông)

b) Ta có: AN = BN (vì N thuộc đường trung trực của AB)

Mà AM = BN (theo giả thiết)

⇒ AN = AM

⇒ $\Delta AMN$ cân cân tại A (đpcm)

c) Tam giác AMO vuông tại O có:

$\widehat{AMO}+\widehat{MAO}=90°$ (hai góc phụ nhau)

⇒ $30°+\widehat{MAO}=90°$

⇒ $\widehat{MAO}=60°$ hay $\widehat{MAB}=60°$

Có: MA = MB (vì M thuộc đường trung trực của AB)

⇒ $\Delta AMB$ là tam giác cân

Mà $\widehat{MAB}=60°$

⇒ $\Delta AMB$ là tam giác đều (đpcm).

B2. Trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng (Kết nối tri thức 2023) có đáp án

I. Nhận biết

Câu 1. Cặp tam giác nào sau đây bằng nhau?

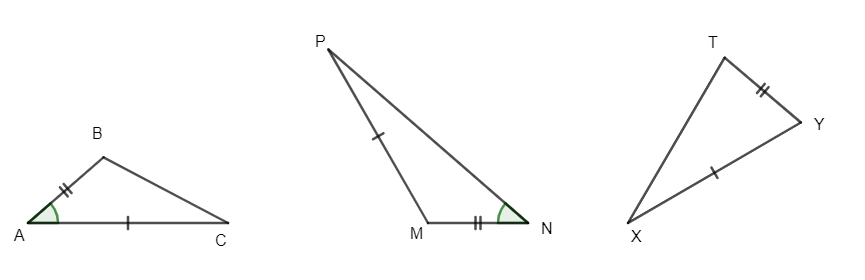
Khẳng định nào sau đây đúng?

A. ∆ABC = ∆MNP;            

B. ∆ABC = ∆XYT;              

C. ∆MNP = ∆XYT;             

D. Không có cặp tam giác nào bằng nhau.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

⦁ Xét ∆ABC và ∆MNP, có:

AB = MN (giả thiết)

AC = MP (giả thiết)

$\widehat{BAC}=\widehat{MNP}$ (giả thiết)

Tuy nhiên hai góc $\widehat{BAC}$ và $\widehat{MNP}$ không xen giữa hai cạnh đã cho.

Suy ra ∆ABC và ∆MNP không bằng nhau. Do đó A sai.

⦁ Xét ∆MNP và ∆XYT, có:

MN = YT (giả thiết)

MP = XY (giả thiết)

Chưa đủ điều kiện để suy ra ∆MNP và ∆XYT bằng nhau. Do đó B sai.

⦁ Xét ∆ABC và ∆XYT, có:

AB = YT (giả thiết)

AC = XY (giả thiết)

Chưa đủ điều kiện để suy ra ∆ABC và ∆XYT bằng nhau. Do đó C sai.

Vì vậy không có cặp tam giác nào bằng nhau.

Vậy chọn đáp án D.

Câu 2. Cho ∆ABC vuông tại B và ∆DEF vuông tại E có AB = DE và BC = EF. Khi đó ∆ABC = ∆DEF theo trường hợp:

A. cạnh huyền – cạnh góc vuông;                 

B. cạnh huyền – góc nhọn;                  

C. cạnh – góc – cạnh;                  

D. góc – cạnh – góc.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Xét ∆ABC và ∆DEF, có:

$\widehat{ABC}=\widehat{DEF}=90°$.

AB = DE (giả thiết)

BC = EF (giả thiết)

Do đó ∆ABC = ∆DEF (c.g.c)

Vậy ta chọn phương án C.

Câu 3. Cho ∆MNP vuông tại P và ∆XYZ vuông tại Z có MP = XZ. Để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện gì?

A. MN = XY;                       

B. MN = YZ;            

C. $\widehat{NMP}=\widehat{ZYX}$;               

D. $\widehat{MNP}=\widehat{XYZ}$.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta thấy MP, XZ lần lượt là cạnh góc vuông của ∆MNP và ∆XYZ.

Do đó để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện hai cạnh huyền của hai tam giác đó bằng nhau. Nghĩa là, MN = XY.

Vậy ta chọn phương án A.

Câu 4. Phát biểu nào sau đây đúng nhất?

A. Tam giác cân là tam giác có hai cạnh bằng nhau;                   

B. Một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân;                    

C. Tam giác đều là tam giác có ba cạnh bằng nhau;                    

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

⦁ Tam giác cân là tam giác có hai cạnh bằng nhau.

Suy ra phương án A đúng.

⦁ Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Suy ra phương án B đúng.

⦁ Tam giác đều là tam giác có ba cạnh bằng nhau.

Suy ra phương án C đúng.

Vậy ta chọn phương án D.

Câu 5. Phát biểu nào dưới đây đúng nhất?

A. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;                

B. Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;   

C. Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;                       

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Phương án A: Phát biểu của trường hợp cạnh góc vuông – góc nhọn kề (hay g.c.g).

Phương án B: Phát biểu của trường hợp cạnh huyền – cạnh góc vuông.

Phương án C: Phát biểu của trường hợp cạnh huyền – góc nhọn.

Vậy ta chọn phương án D.

Câu 6. Cho ∆ABC có AB = BC = 5 cm và $\widehat{C}=60°$. Khi đó ∆ABC là:

A. Tam giác đều;              

B. Tam giác cân tại A;                 

C. Tam giác cân tại B;                 

D. Tam giác vuông cân.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Một tam giác có hai cạnh bằng nhau là tam giác cân.

Tam giác cân có một góc bằng 60° là tam giác đều.

Vì vậy ∆ABC là tam giác đều.

Vậy ta chọn phương án A.

Câu 7. Cho ∆MNP cân tại M và $\widehat{M}=80°$. Số đo của $\widehat{N}$ bằng:

A. 40°;                      

B. 100°;                   

C. 50°;                      

D. 90°.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích: 

Câu 8. Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?

A.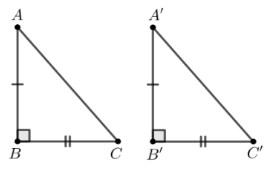 

B.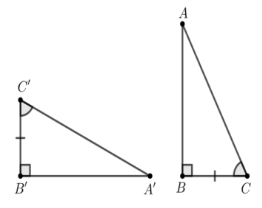 

C.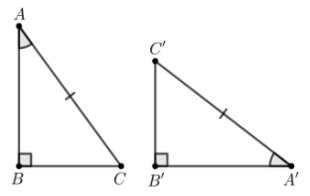 

D.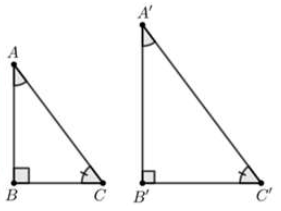 

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

⦁ Xét phương án A:

Xét ∆ABC và ∆A’B’C’, có:

$\widehat{ABC}=\widehat{A^{‘}{B}^{‘}{C}^{‘}}=90°$.

AB = A’B’ (giả thiết)

BC = B’C’ (giả thiết)

Do đó ∆ABC = ∆A’B’C’ (c.g.c)

Vì vậy phương án A có chứa hai tam giác vuông bằng nhau.

⦁ Xét phương án B:

Xét ∆A’B’C’ và ∆ABC, có:

$\widehat{A^{‘}{B}^{‘}{C}^{‘}}=\widehat{ABC}=90°$.

B’C’ = BC (giả thiết)

$\widehat{B^{‘}{C}^{‘}{A}^{‘}}=\widehat{BCA}$ (giả thiết)

Do đó ∆A’B’C’ = ∆ABC (g.c.g)

Vì vậy phương án B có chứa hai tam giác vuông bằng nhau.

⦁ Xét phương án C:

Xét ∆ABC và ∆A’B’C’, có:

$\widehat{ABC}=\widehat{A^{‘}{B}^{‘}{C}^{‘}}=90°$.

AC = A’C’ (giả thiết)

$\widehat{BAC}=\widehat{B^{‘}{A}^{‘}{C}^{‘}}$ (giả thiết)

Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn)

Vì vậy phương án C có chứa hai tam giác vuông bằng nhau.

⦁ Xét phương án D:

Xét ∆ABC và ∆A’B’C’, có:

$\widehat{ABC}=\widehat{A^{‘}{B}^{‘}{C}^{‘}}=90°$.

$\widehat{BAC}=\widehat{B^{‘}{A}^{‘}{C}^{‘}}$ (giả thiết)

$\widehat{BCA}=\widehat{B^{‘}{C}^{‘}{A}^{‘}}$ (giả thiết)

Do đó ∆ABC và ∆A’B’C’ không bằng nhau do không có trường hợp bằng nhau góc – góc – góc.

Vậy ta chọn phương án D.

Câu 9. Tổng ba góc trong một tam giác bất kì luôn bằng:

A. 90°;                      

B. 180°;                   

C. 270°;                   

D. 360°.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Vì tổng ba góc trong một tam giác luôn bằng 180°.

Nên ta chọn phương án B.

Câu 10. Đường trung trực của một đoạn thẳng là:

A. Đường thẳng đi qua trung điểm của đoạn thẳng đó;                       

B. Đường thẳng vuông góc với đoạn thẳng đó;               

C. Đường thẳng vừa đi qua trung điểm, vừa vuông góc với đoạn thẳng đó;                    

D. Đường thẳng song song với đoạn thẳng đó.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.

Vậy ta chọn phương án C.

II. Thông hiểu

Câu 1. Cho ∆ABC có AB = AC. Gọi D, E là hai điểm thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Khẳng định nào sau đây đúng nhất?

A. BE = CD;            

B. ∆ABE = ∆ACD;             

C. $\widehat{EAB}=\widehat{DAC}$;                

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

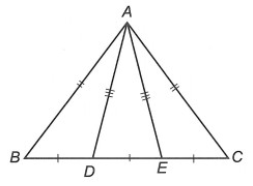
⦁ Ta có BD = EC (giả thiết)

Suy ra BD + DE = DE + EC.

Khi đó BE = CD.

Vì vậy phương án A đúng.

⦁ Xét ∆ABE và ∆ACD, có:

AB = AC (giả thiết)

AD = AE (giả thiết)

BE = CD (chứng minh trên)

Do đó ∆ABE = ∆ACD (c.c.c)

Vì vậy phương án B đúng.

⦁ Ta có ∆ABE = ∆ACD (chứng minh trên)

Suy ra $\widehat{EAB}=\widehat{DAC}$ (cặp góc tương ứng)

Do đó phương án C đúng.

Vậy ta chọn phương án D.

Câu 2. Cho hình vẽ sau. Biết AB // CD và AD // BC.

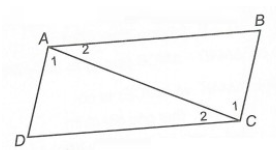
Hình vẽ trên có mấy cặp tam giác bằng nhau?

A. 0;              

B. 1;              

C. 2;              

D. 3.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Xét ∆ABC và ∆CDA, có:

AC là cạnh chung.

$\widehat{A_1}=\widehat{C_1}$ (do AD // BC và hai góc này ở vị trí so le trong)

$\widehat{A_2}=\widehat{C_2}$ (do AB // DC và hai góc này ở vị trí so le trong)

Do đó ∆ABC = ∆CDA (g.c.g)

Vậy có 1 cặp tam giác bằng nhau.

Do đó ta chọn phương án B.

Câu 3. Cho ∆MNP có $\widehat{M}=80°$, biết $\widehat{N}-\widehat{P}=40°$. Khi đó số đo của $\widehat{N}$ bằng:

A. 75°;                      

B. 45°;                      

C. 70°;                      

D. 60°.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

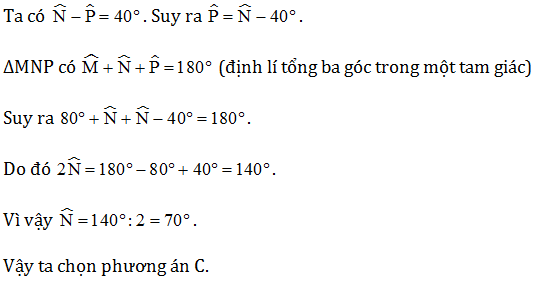
Câu 4. Cho ∆ABC và ∆MNP bằng nhau. Biết số đo các góc như hình vẽ sau:

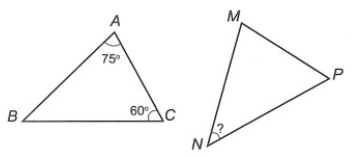
Số đo của $\widehat{MNP}$ bằng:

A. 60°;                      

B. 45°;                      

C. 30°;                      

D. 75°.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}=180°-75°-60°=45°$.

Ta có ∆ABC = ∆MNP (giả thiết)

Suy ra $\widehat{N}=\widehat{B}=45°$ (cặp góc tương ứng)

Vậy ta chọn phương án B.

Câu 5. Cho hình vẽ bên.

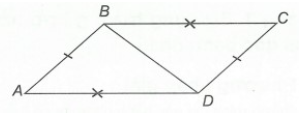
Kết luận nào sau đây đúng?

A. ∆ABD = ∆BCD;            

B. ∆BAD = ∆CDB;            

C. ∆ABD = ∆CBD;             

D. ∆ABD = ∆CDB.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Xét ∆ABD và ∆CDB, có:

BD là cạnh chung.

AB = CD (giả thiết)

AD = CB (giả thiết)

Do đó ∆ABD = ∆CDB (c.c.c)

Vậy ta chọn phương án D.

Câu 6. Cho hình bên.

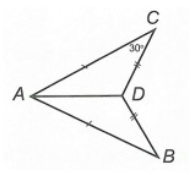
Số đo của $\widehat{ABD}$ bằng:

A. 30°;                      

B. 45°;                      

C. 60°;                      

D. 85°.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

AB = AC (giả thiết)

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.c.c)

Suy ra $\widehat{ABD}=\widehat{ACD}=30°$ (cặp góc tương ứng)

Vậy ta chọn phương án A.

Câu 7. Cho ∆ABC có AB = AC. Gọi AM là tia phân giác của  (M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).

Cho các khẳng định sau:

(I) $\widehat{BMD}=\widehat{CME}$;             

(II) ∆MBD = ∆MCE;                    

(III) AD = AE ;                   

Gọi m là số kết luận đúng và n là số kết luận sai. Giá trị của m và n là:

A. m = 0 và n = 1;            

B. m = 2 và n = 1;            

C. m = 3 và n = 0;             

D. m = 1 và n = 2.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

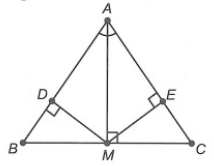
Xét ∆AMD và ∆AME, có:

AM là cạnh chung.

$\widehat{ADM}=\widehat{AEM}=90°$.

$\widehat{DAM}=\widehat{EAM}$ (AM là phân giác của $\widehat{DAE}$)

Do đó ∆AMD = ∆AME (cạnh huyền – góc nhọn)

Suy ra AD = AE và MD = ME (các cặp cạnh tương ứng)

Do đó (III) đúng.

Ta có AB = AC (giả thiết) và AD = AE (chứng minh trên)

Suy ra AB – AD = AC – AE.

Khi đó DB = EC.

Xét ∆MBD và ∆MCE, có:

$\widehat{BDM}=\widehat{CEM}=90°$.

DB = EC (chứng minh trên)

MD = ME (chứng minh trên)

Do đó ∆MBD = ∆MCE (c.g.c). Do đó (II) đúng.

Suy ra $\widehat{BMD}=\widehat{CME}$ (cặp góc tương ứng). Do đó (I) đúng.

Vậy ta có 3 phát biểu đúng và 0 phát biểu sai hay m = 3 và n = 0.

Vậy ta chọn phương án C.

Câu 8. Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, $\widehat{A}=60°$. Tính cạnh BC.

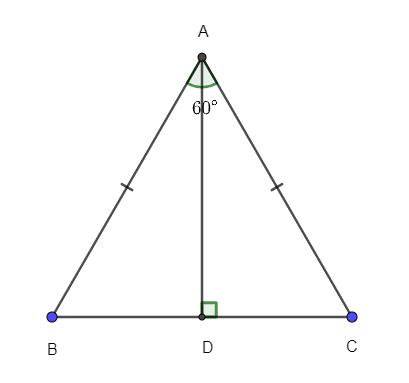
A. BC = 6 cm;                     

B. BC = 1,5 cm;                 

C. BC = 9 cm;                     

D. BC = 3cm.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

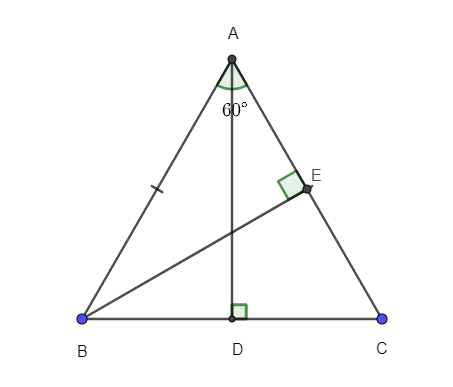
Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

$\widehat{ADB}=\widehat{ADC}=90°$.

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.g.c)

$\Rightarrow \widehat{ABD}=\widehat{ACD}$ (cặp góc tương ứng)

Xét tam giác ABC, có: $\widehat{ABD}+\widehat{ACD}+\widehat{BAC}=180°$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \widehat{ABD}=\widehat{ACD}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-60°}{2}=60°$.

Kẻ BE vuông góc với AC.

Xét ∆BEA và ∆BEC, có:

$\widehat{BEA}=\widehat{BEC}=90°$

BE là cạnh chung

$\widehat{ABE}=\widehat{CBE}=90°-60°=30°$

Do đó ∆BEA = ∆BEC (cạnh góc vuông – góc nhọn)

Suy ra AB = BC

Mà AB = 3cm nên BC = 3cm.

Vậy chọn đáp án D.

Câu 9. Cho ∆ABC có AB = AC ($\widehat{A}<90°$). Kẻ BD vuông góc với AC (D ∈ AC) và CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE.  

Cho bảng sau:

A	B
a. ∆AEC	1. ∆HDC
b. ∆HEB	2. ∆CDB
c. ∆BEC	3. ∆ADB

Ghép các ý ở cột A với cột B để được một đẳng thức đúng?

A. a – 2; b – 1; c – 3;                    

B. a – 1; b – 3; c – 2;                    

C. a – 3; b – 1; c – 2;                    

D. a – 2; c – 1; b – 3.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

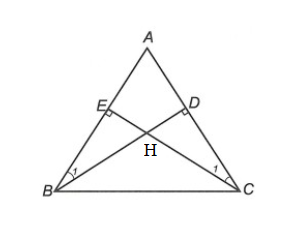
+) Xét ∆ADB và ∆AEC, có:

AB = AC (giả thiết)

$\widehat{ADB}=\widehat{AEC}=90°$.

$\widehat{BAC}$ là góc chung.

Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn)

Khi đó a – 3.

+) Vì ∆ADB = ∆AEC nên $\widehat{B_1}=\widehat{C_1}$ (cặp góc tương ứng) và AD = BE (cặp cạnh tương ứng)

Ta có: AD + DC = AC, AE + EB = AB

Mà AB = AC, AD = BE nên DC = EB.

Xét ∆HEB và ∆HDC, có:

$\widehat{HEB}=\widehat{HDC}=90°$

BE = DC

$\widehat{B_1}=\widehat{C_1}$ 

Suy ra ∆HEB = ∆HDC (g – c – g)

Do đó b – 1.

+) Xét ∆BEC và ∆CDB, có:

$\widehat{BEC}=\widehat{CDB}=90°$

BE = DC

BC là cạnh chung

Suy ra ∆BEC = ∆CDB (cạnh góc vuông – cạnh huyền)

Do đó c – 2.

Vậy a – 3, b – 1, c – 2.

Chọn đáp án C.

Câu 10. Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai?

A. AM = DM;                      

B. ∆ABM = ∆ADM ;                     

C. $\widehat{MAD}=\widehat{MDA}$;             

D. A, B, C sai.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

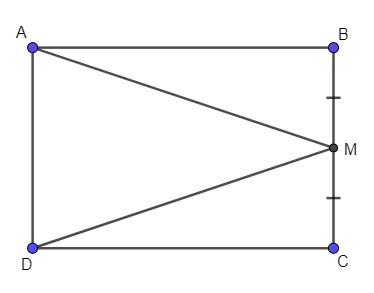
Xét ∆ABM và ∆DCM, có:

AB = DC (ABCD là hình chữ nhật)

$\widehat{ABM}=\widehat{DCM}=90°$ (ABCD là hình chữ nhật)

MB = MC (giả thiết)

Do đó ∆ABM = ∆DCM (c.g.c)

Suy ra AM = DM và $\widehat{BAM}=\widehat{CDM}$ (cặp cạnh và cặp góc tương ứng)

Ta có: $\widehat{MAD}+\widehat{BAM}=\widehat{MDA}+\widehat{CDM}=90°$ (các cặp góc phụ nhau)

Suy ra $\widehat{MAD}=\widehat{MDA}$

Vì vậy phương án A, B, C đều đúng.

Vậy ta chọn phương án D.

Câu 11. Cho hình vẽ bên.

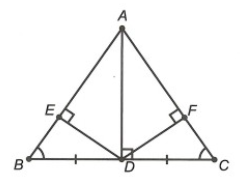
Khẳng định nào sau đây sai?

A. ∆AED = ∆AFD;             

B. ∆BED = ∆CFD;             

C. ∆ADB = ∆ADC;             

D. ∆ADE = ∆AFD.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

⦁ Xét phương án B:

Xét ∆BED và ∆CFD, có:

$\widehat{BED}=\widehat{CFD}=90°$.

BD = CD (giả thiết)

$\widehat{EBD}=\widehat{FCD}$ (giả thiết)

Do đó ∆BED = ∆CFD (cạnh huyền – góc nhọn)

Vì vậy phương án B đúng.

⦁ Xét ∆AED và ∆AFD, có:

AD là cạnh chung.

ED = FD (∆BED = ∆CFD)

$\widehat{AED}=\widehat{AFD}=90°$.

Do đó ∆AED = ∆AFD (cạnh huyền – cạnh góc vuông)

Vì vậy phương án A đúng, phương án D sai (do viết sai thứ tự các đỉnh).

⦁ Xét phương án C:

Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

$\widehat{ADB}=\widehat{ADC}=90°$.

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.g.c)

Vì vậy phương án C đúng.

Vậy ta chọn phương án D.

Câu 12. Cho ∆ABC vuông tại A có hai đường trung trực của hai cạnh AB và AC cắt nhau tại D. Vị trí của điểm D là:

A. D là trung điểm BC;   

B. D là trung điểm của AB;                   

C. D là trung điểm của AC;                   

D. D là điểm trong tam giác ABC.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

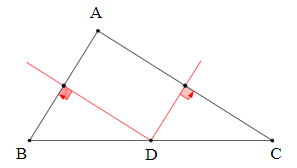
Gọi điểm M là giao điểm của đường trung trực của AB với BC.

Vì M thuộc trung trực của đoạn thẳng AB nên MA = MB.

Suy ra tam giác MAB cân tại M

⇒ $\widehat{B}=\widehat{MAB}$

Ta có: $\widehat{B}+\widehat{C}=90°$ và $\widehat{MAB}+\widehat{MAC}=90°$

⇒ $\widehat{C}=\widehat{MAC}$

⇒ Tam giác MAC cân tại M

⇒ MA = MC ⇒ M thuộc đường trung trực của đoạn thẳng AC

Vậy M là giao điểm của hai đường trung trực của AB và AC hay ta có M trùng D.

Ta có DA = DB, DA = DC nên DB = DC

Vậy D là trung điểm của đoạn thẳng BC.

Câu 13. Cho tam giác ABC cân tại A, có $\widehat{A}=24°$. Trên tia đối của tia BC lấy điểm D sao cho $\widehat{ADB}=30°$, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính $\widehat{BAE}$?

 

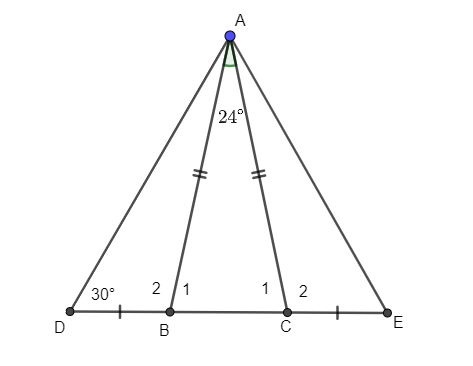
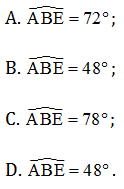
Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

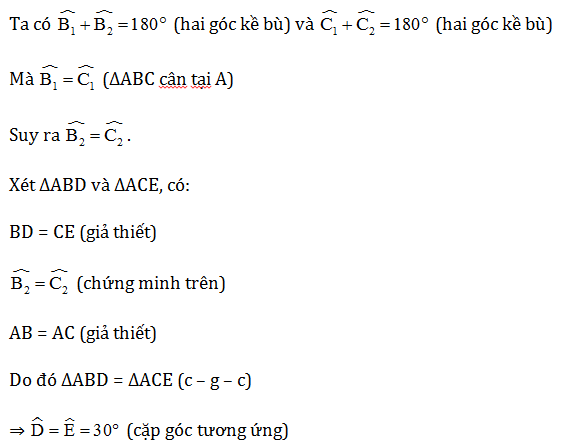
Xét tam giác ABE, có:

$\widehat{BAE}+\widehat{B_1}+\widehat{E}=180°$(định lí tổng ba góc trong tam giác)

$\widehat{BAE}=180°-\widehat{B_1}-\widehat{E}=180°-78°-30°=72°$

Vậy ta chọn phương án A.

Câu 14. Cho đoạn thẳng CD. Gọi A là trung điểm của CD. Kẻ một đường thẳng vuông góc với CD tại A. Trên đường thẳng đó, lấy điểm B sao cho $\widehat{BCD}=60°$. Khi đó ∆BCD là tam giác gì?

A. Tam giác tù;                  

B. Tam giác đều;              

C. Tam giác vuông cân;              

D. Tam giác vuông.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích: 

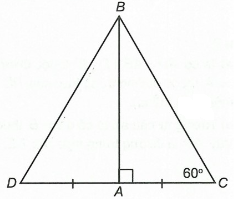
Ta có AC = AD (A là trung điểm của CD) và AB ⊥ CD (giả thiết)

Suy ra AB là đường trung trực của đoạn thẳng CD.

Do đó BD = BC (tính chất đường trung trực của một đoạn thẳng)

Vì vậy ∆BCD cân tại B.

Mà ∆BCD có $\widehat{C}=60°$ (giả thiết)

Do đó ∆BCD là tam giác đều.

Vậy ta chọn phương án B.

Câu 15. Cho ∆ABC có $\widehat{B}=2\widehat{C}$. Kẻ đường phân giác BD, từ D kẻ DE //BC (E ∈ AB). Số tam giác cân là:

A. 0;              

B. 1;              

C. 2;              

D. 3.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

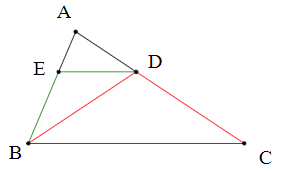
∆ABC có BD là đường phân giác.

Suy ra $\widehat{ABD}=\widehat{DBC}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}.2\widehat{ACB}=\widehat{ACB}$.

Do đó ∆BCD cân tại D.

Ta có BD // BC (giả thiết)

Suy ra $\widehat{EDB}=\widehat{DBC}$ (cặp góc so le trong)

Mà $\widehat{EBD}=\widehat{DBC}$ (chứng minh trên)

Do đó $\widehat{EDB}=\widehat{EBD}$.

Suy ra ∆BED cân tại E.

Do đó có 2 tam giác cân

Vậy ta chọn phương án C.

Xem thêm các bài tóm tắt lý thuyết Toán 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Lý thuyết Toán 7 Chương 4: Tam giác bằng nhau

Lý thuyết Bài 17: Thu thập và phân loại dữ liệu

Lý thuyết Bài 18: Biểu đồ hình quạt tròn

Lý thuyết Bài 19: Biểu đồ đoạn thẳng

Lý thuyết Toán 7 Chương 5 : Thu thập và biểu diễn dữ liệu