Hàm số y = f(x) = \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có tập xác định D là: A. D = [1; + ∞); B. D = ℝ \ {– 3; 3}; C. D = [1; + ∞) \ {3}; D. D = [3; + ∞).

By 0

Câu hỏi:

Hàm số y = f(x) = \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có tập xác định D là:
A. D = [1; + ∞);
B. D = ℝ \ {– 3; 3};
C. D = [1; + ∞) \ {3};
D. D = [3; + ∞).

Trả lời:

Hướng dẫn giải
Đáp án đúng là: C
Biểu thức \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có nghĩa khi \(\left\{ \begin{array}{l}x – 1 > 0\\{x^2} – 9 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x \ne \pm 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x \ne 3\end{array} \right.\).
Vậy tập xác định của hàm số là D = [1; + ∞) \ {3}.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Một hàm số có thể được cho bằng: A. Bảng giá trị của hàm số; B. Đồ thị của hàm số; C. Công thức của hàm số; D. Tất cả đều đúng.

    Câu hỏi:

    Một hàm số có thể được cho bằng:
    A. Bảng giá trị của hàm số;
    B. Đồ thị của hàm số;
    C. Công thức của hàm số;
    D. Tất cả đều đúng.

    Trả lời:

    Hướng dẫn giải
    Đáp án đúng là: D
    Một hàm số có thể được cho bằng bảng giá trị của hàm số, hoặc bằng đồ thị của hàm số hoặc bằng công thức của hàm số. Vậy các đáp án A, B, C đều đúng, ta chọn đáp án D.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Cho hàm số y = f(x) = 2(x + 1)(x – 3) + 2x – 6. Giá trị của hàm số khi x = 3 là: A. 8; B. 0; C. – 6; D. 3.

    Câu hỏi:

    Cho hàm số y = f(x) = 2(x + 1)(x – 3) + 2x – 6. Giá trị của hàm số khi x = 3 là:
    A. 8;
    B. 0;
    C. – 6;
    D. 3.

    Trả lời:

    Hướng dẫn giải
    Đáp án đúng là: B
    Thay x = 3 vào hàm số ta được:
    f(3) = 2.(3 + 1).(3 – 3) + 2 . 3 – 6 = 0 + 6 – 6 = 0.
    Vậy giá trị của hàm số khi x = 3 là 0.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai? A. y = f(x) = \(\sqrt 3 \)x2 + x – 4; B. y = f(x) = x2 + \(\frac{1}{x}\) – 5; C. y = f(x) = – 2x(x – 1); D. y = f(x) = 2(x2 + 1) + 3x – 1.

    Câu hỏi:

    Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?
    A. y = f(x) = \(\sqrt 3 \)x2 + x – 4;
    B. y = f(x) = x2 + \(\frac{1}{x}\) – 5;
    C. y = f(x) = – 2x(x – 1);
    D. y = f(x) = 2(x2 + 1) + 3x – 1.

    Trả lời:

    Hướng dẫn giải

    Đáp án đúng là: B
    +) Hàm số y = f(x) = \(\sqrt 3 \)x2 + x – 4, đây là hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = \(\sqrt 3 \) ≠ 0, b = 1, c = – 4.
    +) Hàm số y = f(x) = x2 + \(\frac{1}{x}\) – 5 không phải là hàm số bậc hai vì nó không có dạng y = ax2 + bx + c.
    +) Hàm số y = f(x) = – 2x(x – 1) hay y = f(x) = – 2×2 + 2x, đây là hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = – 2 ≠ 0, b = 2, c = 0.
    +) Hàm số y = f(x) = 2(x2 + 1) + 3x – 1 hay y = f(x) = 2×2 + 3x + 1, đây hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = 2 ≠ 0, b = 3, c = 1.
    Vậy trong các hàm số đã cho, chỉ có hàm số ở đáp án B không phải là hàm số bậc hai.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Tập giá trị của hàm số y = f(x) = – 2×2 + \(\sqrt 2 \)x + 1 là A. T = \(\left( { – \frac{5}{4}; + \infty } \right)\); B. T = \(\left[ { – \frac{5}{4}; + \infty } \right)\); C. T = \(\left( { – \infty ;\frac{5}{4}} \right)\); D. T = \(\left( { – \infty ;\,\frac{5}{4}} \right]\).

    Câu hỏi:

    Tập giá trị của hàm số y = f(x) = – 2x2 + \(\sqrt 2 \)x + 1 là
    A. T = \(\left( { – \frac{5}{4}; + \infty } \right)\);
    B. T = \(\left[ { – \frac{5}{4}; + \infty } \right)\);
    C. T = \(\left( { – \infty ;\frac{5}{4}} \right)\);
    D. T = \(\left( { – \infty ;\,\frac{5}{4}} \right]\).

    Trả lời:

    Hướng dẫn giải
    Đáp án đúng là: D
    Do hàm số y = f(x) = – 2x2 + \(\sqrt 2 \)x + 1 là hàm số bậc hai nên đồ thị hàm số này là parabol có tọa độ đỉnh S là
    xS = \( – \frac{b}{{2a}}\) \( = – \frac{{\sqrt 2 }}{{2.\left( { – 2} \right)}}\) = \(\frac{{\sqrt 2 }}{4}\), yS = \( – 2.{\left( {\frac{{\sqrt 2 }}{4}} \right)^2} + \sqrt 2 .\frac{{\sqrt 2 }}{4} + 1 = \frac{5}{4}\) hay S\(\left( {\frac{{\sqrt 2 }}{4};\,\frac{5}{4}} \right)\).
    Lại có hàm số có hệ số a = – 2 < 0 nên bề lõm của parabol hướng xuống dưới, do đó đỉnh S là điểm cao nhất của đồ thị hàm số.
    Vậy tập giá trị của hàm số đã cho là: T = \(\left( { – \infty ;\frac{5}{4}} \right)\).

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Hàm số y = f(x) = –(x + 2)(x – 4) đồng biến trên khoảng: A. (– ∞; – 1); B. (1; + ∞); C. (– ∞; 1); D. (– 1; + ∞).

    Câu hỏi:

    Hàm số y = f(x) = –(x + 2)(x – 4) đồng biến trên khoảng:
    A. (– ∞; – 1);
    B. (1; + ∞);
    C. (– ∞; 1);
    D. (– 1; + ∞).

    Trả lời:

    Hướng dẫn giải
    Đáp án đúng là: C
    Ta có: – (x + 2)(x – 4) = – x2 + 4x – 2x + 8 = – x2 + 2x + 8.
    Do đó ta có hàm số y = f(x) = – x2 + 2x + 8.
    Đây là hàm số bậc hai nên đồ thị hàm số là parabol với tọa độ đỉnh S là
    xS = \( – \frac{b}{{2a}} = – \frac{2}{{2.\left( { – 1} \right)}} = 1\), yS = – 12 + 2 . 1 + 8 = 9 hay S(1; 9).
    Do hệ số a = – 1 < 0 nên ta có bảng biến thiên:
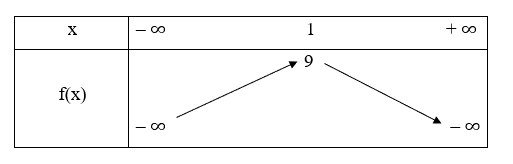
    Media VietJack
    Vậy hàm số đã cho đồng biến trên khoảng (– ∞; 1).

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu