Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng 45°. Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?

Câu hỏi:

Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng 45°. Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?

Trả lời:

Hướng dẫn giải

Theo giả thiết bài toán, ta có phương trình chuyển động của lao sau khi ném là:
\(y = \frac{{ – g{x^2}}}{{2v_0^2\,co{s^2}\alpha }} + \tan \alpha \,.\,x + {y_0}\) \( = \frac{{ – 10{x^2}}}{{2\,\,.\,\,v_0^2\,.\,co{s^2}45^\circ }} + \tan 45^\circ .x + 0,9\)\( = – \frac{{10}}{{v_0^2}}{x^2} + x + 0,9\).

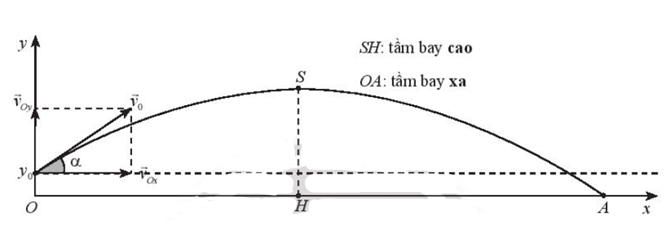
Mặt khác, lao được ném đi đạt độ xa 90 m, tức là OA = 90. Nói các khác điểm A(90; 0) thuộc đồ thị hàm số nên ta có: f(90) = 0 hay  \( – \frac{{10}}{{v_0^2}}{.90^2} + 90 + 0,9 = 0\)\( \Leftrightarrow v_0^2 = \frac{{90000}}{{101}}\).
Suy ra v₀ ≈ 29,85 (m/s).
Vậy vận tốc đầu của lao khi được ném đi xấp xỉ bằng 29,85 m/s.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một hàm số có thể được cho bằng: A. Bảng giá trị của hàm số; B. Đồ thị của hàm số; C. Công thức của hàm số; D. Tất cả đều đúng.
   
   

   Câu hỏi:
   

   Một hàm số có thể được cho bằng:
   A. Bảng giá trị của hàm số;
   B. Đồ thị của hàm số;
   C. Công thức của hàm số;
   D. Tất cả đều đúng.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Một hàm số có thể được cho bằng bảng giá trị của hàm số, hoặc bằng đồ thị của hàm số hoặc bằng công thức của hàm số. Vậy các đáp án A, B, C đều đúng, ta chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y = f(x) = 2(x + 1)(x – 3) + 2x – 6. Giá trị của hàm số khi x = 3 là: A. 8; B. 0; C. – 6; D. 3.
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) = 2(x + 1)(x – 3) + 2x – 6. Giá trị của hàm số khi x = 3 là:
   A. 8;
   B. 0;
   C. – 6;
   D. 3.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Thay x = 3 vào hàm số ta được:
   f(3) = 2.(3 + 1).(3 – 3) + 2 . 3 – 6 = 0 + 6 – 6 = 0.
   Vậy giá trị của hàm số khi x = 3 là 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số y = f(x) = \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có tập xác định D là: A. D = [1; + ∞); B. D = ℝ \ {– 3; 3}; C. D = [1; + ∞) \ {3}; D. D = [3; + ∞).
   
   

   Câu hỏi:
   

   Hàm số y = f(x) = \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có tập xác định D là:
   A. D = [1; + ∞);
   B. D = ℝ \ {– 3; 3};
   C. D = [1; + ∞) \ {3};
   D. D = [3; + ∞).

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Biểu thức \(\sqrt {x – 1} + \frac{1}{{{x^2} – 9}}\) có nghĩa khi \(\left\{ \begin{array}{l}x – 1 > 0\\{x^2} – 9 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x \ne \pm 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x \ne 3\end{array} \right.\).
   Vậy tập xác định của hàm số là D = [1; + ∞) \ {3}.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai? A. y = f(x) = \(\sqrt 3 \)x2 + x – 4; B. y = f(x) = x2 + \(\frac{1}{x}\) – 5; C. y = f(x) = – 2x(x – 1); D. y = f(x) = 2(x2 + 1) + 3x – 1.
   
   

   Câu hỏi:
   

   Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?
   A. y = f(x) = \(\sqrt 3 \)x² + x – 4;
   B. y = f(x) = x² + \(\frac{1}{x}\) – 5;
   C. y = f(x) = – 2x(x – 1);
   D. y = f(x) = 2(x² + 1) + 3x – 1.

   Trả lời:

   Hướng dẫn giải

   Đáp án đúng là: B
   +) Hàm số y = f(x) = \(\sqrt 3 \)x2 + x – 4, đây là hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = \(\sqrt 3 \) ≠ 0, b = 1, c = – 4.
   +) Hàm số y = f(x) = x2 + \(\frac{1}{x}\) – 5 không phải là hàm số bậc hai vì nó không có dạng y = ax2 + bx + c.
   +) Hàm số y = f(x) = – 2x(x – 1) hay y = f(x) = – 2×2 + 2x, đây là hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = – 2 ≠ 0, b = 2, c = 0.
   +) Hàm số y = f(x) = 2(x2 + 1) + 3x – 1 hay y = f(x) = 2×2 + 3x + 1, đây hàm số bậc hai do nó có dạng y = ax2 + bx + c với a = 2 ≠ 0, b = 3, c = 1.
   Vậy trong các hàm số đã cho, chỉ có hàm số ở đáp án B không phải là hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tập giá trị của hàm số y = f(x) = – 2×2 + \(\sqrt 2 \)x + 1 là A. T = \(\left( { – \frac{5}{4}; + \infty } \right)\); B. T = \(\left[ { – \frac{5}{4}; + \infty } \right)\); C. T = \(\left( { – \infty ;\frac{5}{4}} \right)\); D. T = \(\left( { – \infty ;\,\frac{5}{4}} \right]\).
   
   

   Câu hỏi:
   

   Tập giá trị của hàm số y = f(x) = – 2x² + \(\sqrt 2 \)x + 1 là
   A. T = \(\left( { – \frac{5}{4}; + \infty } \right)\);
   B. T = \(\left[ { – \frac{5}{4}; + \infty } \right)\);
   C. T = \(\left( { – \infty ;\frac{5}{4}} \right)\);
   D. T = \(\left( { – \infty ;\,\frac{5}{4}} \right]\).

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Do hàm số y = f(x) = – 2x² + \(\sqrt 2 \)x + 1 là hàm số bậc hai nên đồ thị hàm số này là parabol có tọa độ đỉnh S là
   x_S = \( – \frac{b}{{2a}}\) \( = – \frac{{\sqrt 2 }}{{2.\left( { – 2} \right)}}\) = \(\frac{{\sqrt 2 }}{4}\), y_S = \( – 2.{\left( {\frac{{\sqrt 2 }}{4}} \right)^2} + \sqrt 2 .\frac{{\sqrt 2 }}{4} + 1 = \frac{5}{4}\) hay S\(\left( {\frac{{\sqrt 2 }}{4};\,\frac{5}{4}} \right)\).
   Lại có hàm số có hệ số a = – 2 < 0 nên bề lõm của parabol hướng xuống dưới, do đó đỉnh S là điểm cao nhất của đồ thị hàm số.
   Vậy tập giá trị của hàm số đã cho là: T = \(\left( { – \infty ;\frac{5}{4}} \right)\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====