Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là A. 8 cm. B. 64 cm. C. 30 cm. D. 16 cm.

Câu hỏi:

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là
A. 8 cm.
B. 64 cm.
C. 30 cm.
D. 16 cm.

Trả lời:

Đáp án đúng là: D
• Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra $MN=\frac{1}{2}BC$.
• Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra $NP=\frac{1}{2}AB$.
• Vì M, P lần lượt là trung điểm của các cạnh AB, BC nên NP là đường trung bình của tam giác ABC suy ra $MP=\frac{1}{2}AC$.
Chu vi tam giác ABC bằng: AB + BC + CA = 32 (cm).
Chu vi tam giác MNP bằng:
$MN+NP+MP=\frac{1}{2}BC+\frac{1}{2}AB+\frac{1}{2}AC$
$=\frac{1}{2}(AB+BC+CA)=\frac{1}{2}.32=16$ (cm)
Vậy chu vi tam giác MNP bằng 16 cm.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Độ dài x trong Hình 4.31 bằng A. 2,75 B. 2. C. 2,25. D. 3,75.
   
   

   Câu hỏi:
   

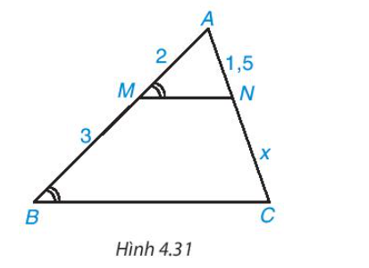
   Độ dài x trong Hình 4.31 bằng
   
   A. 2,75
   B. 2.
   C. 2,25.
   D. 3,75.

   Trả lời:

   Đáp án đúng là: C
   Trong Hình 4.31 có $\widehat{AMN}=\widehat{ABC}$ mà hai góc này ở vị trí đồng vị nên MN // BC.
   Áp dụng định lí Thalès vào tam giác ABC, ta có:
   $\frac{AM}{BM}=\frac{AN}{CN}$ hay $\frac{2}{3}=\frac{1,5}{x}$.
   Suy ra $x=\frac{1,5.3}{2}=2,25$.
   Vậy x = 2,25.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng A. 3,5 cm. B. 7 cm. C. 10 cm. D. 15 cm.
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng
   A. 3,5 cm.
   B. 7 cm.
   C. 10 cm.
   D. 15 cm.

   Trả lời:

   Đáp án đúng là: B
   Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra $HK=\frac{1}{2}AB$.
   Do đó AB = 2HK = 2 . 3,5 = 7 (cm).
   Vậy AB = 7 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng A. 4 cm. B. 5 cm. C. 6 cm. D. 7 cm.
   
   

   Câu hỏi:
   

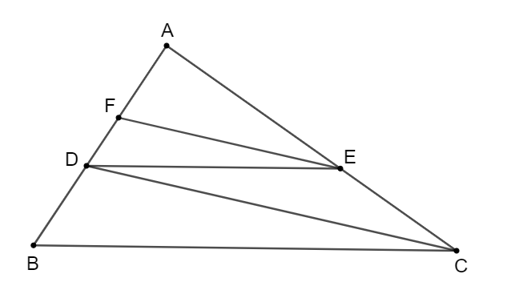
   Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng
   A. 4 cm.
   B. 5 cm.
   C. 6 cm.
   D. 7 cm.

   Trả lời:

   
   Đáp án đúng là: A
   Áp dụng định lí Thalès:
   • Với DE // BC (E ∈ AC) ta có: $\frac{AD}{AB}=\frac{AE}{AC}=\frac{9}{12}=\frac{2}{3}$;
   • Với EF // CD (F ∈ AB) ta có: $\frac{AF}{AD}=\frac{AE}{AC}=\frac{2}{3}$.
   Suy ra $AF=\frac{2}{3}AD=\frac{2}{3}.6=4$ (cm).
   Vậy AF = 4 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là A. 3 cm. B. 6 cm. C. 9 cm. D. 12 cm.
   
   

   Câu hỏi:
   

   Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là
   A. 3 cm.
   B. 6 cm.
   C. 9 cm.
   D. 12 cm.

   Trả lời:

   Đáp án đúng là: C
   Vì tam giác ABC cân tại A nên AB = AC = 15 cm.
   Theo đề bài, BD là tia phân giác của $\widehat{ABC}$, áp dụng tính chất đường phân giác vào tam giác ABC, ta có:
   $\frac{AB}{BC}=\frac{AD}{CD}=\frac{15}{10}=\frac{3}{2}$ suy ra $\frac{AD}{3}=\frac{CD}{2}$.
   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
   $\frac{AD}{3}=\frac{CD}{2}=\frac{AD+CD}{3+2}=\frac{AC}{5}=\frac{15}{5}=3$.
   Do đó AD = 3 . 3 = 9 (cm).
   Vậy AD = 9 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.
   
   

   Câu hỏi:
   

   Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.

   Trả lời:

   
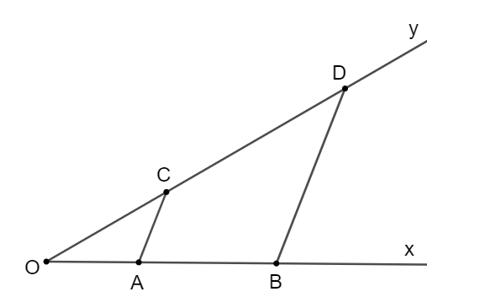
   Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.
   Áp dụng định lí Thalès vào tam giác OBD, ta có:
   $\frac{OA}{OB}=\frac{OC}{OD}$ hay $\frac{2}{5}=\frac{3}{OD}$.
   Suy ra $OD=\frac{5.3}{2}=7,5$ (cm)
   Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).
   Vậy CD = 4,5 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====