Câu hỏi:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm \(y = {x^2}\) và \(y = \frac{{2x}}{{x – 1}}\) là \(S = a + b\ln 2\) với a, b là những số hữu tỷ. Giá trị của \(a + b\) là
A. \( – \frac{1}{3}\).
Đáp án chính xác
B. 2.
C. \( – \frac{2}{3}\).
D. 1.
Trả lời:
Hướng dẫn giải
Phương trình hoành độ giao điểm của \(\left( {{C_1}} \right)\): \(y = {x^2}\) và \(\left( {{C_2}} \right)\): \(y = \frac{{2x}}{{x – 1}}\) là
\({x^2} = \frac{{2x}}{{x – 1}}\left( {x \ne 1} \right) \Rightarrow {x^3} – {x^2} – 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = – 1\\x = 2\end{array} \right.\)
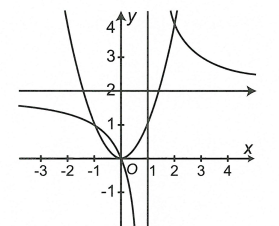
Diện tích hình phẳng cần tìm là:
\(S = \int\limits_{ – 1}^0 {\left( {\frac{{2x}}{{x – 1}} – {x^2}} \right)dx} = \int\limits_{ – 1}^0 {\left( {2 + \frac{2}{{x – 1}} – {x^2}} \right)dx} = \left( {2x + 2\ln \left| {x – 1} \right| – \frac{{{x^3}}}{3}} \right)\left| \begin{array}{l}^0\\_{ – 1}\end{array} \right. = \frac{5}{3} – 2\ln 2\)
Suy ra \(a = \frac{5}{3}\) và \(b = – 2\)
Vậy \(a + b = – \frac{1}{3}\)
Chọn A.
====== **** mời các bạn xem câu tiếp bên dưới **** =====