Câu hỏi:
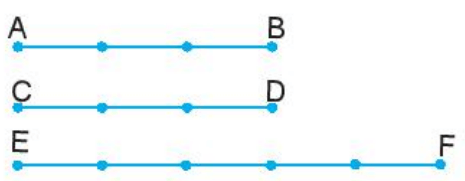
Hãy đo độ dài (đơn vị milimét) rồi sắp xếp các đoạn thẳng trong Hình 8.34 theo thứ tự tăng dần của độ dài.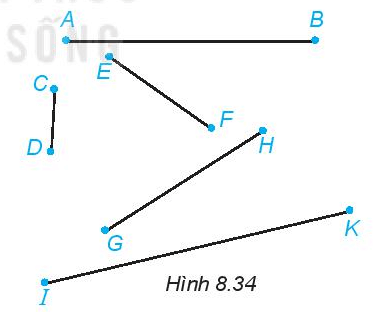
Trả lời:
Sau khi đo độ dài các đoạn thẳng có trong hình 8.34, ta có:CD = 10 mm; AB = 42 mm; EF = 21 mm; GH = 32 mm; IK = 53 mmVì 10 < 21 < 32 < 42 < 53 nên CD < EF < GH < AB < IK.Vậy sắp xếp theo thứ tự tăng dần độ dài đoạn thẳng: CD; EF; GH; AB; IK.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
A. Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng
1. Đoạn thẳng
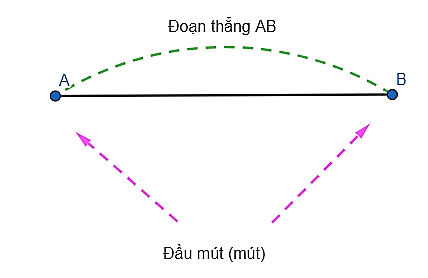
Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa A và B.
Đoạn thẳng AB còn gọi là đoạn thẳng BA.
Hai điểm A, B gọi là hai đầu mút (hoặc hai đầu) của đoạn thẳng AB.
Ta có hình vẽ:
Ví dụ 1. Kể tên các đoạn thẳng có trong hình vẽ dưới đây:
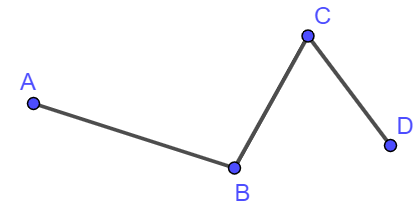
Lời giải:
Cứ hai điểm bất kỳ được nối với nhau sẽ tạo thành một đoạn thẳng.
Trong hình vẽ trên có:
– Điểm A nối với điểm B tạo thành đoạn thẳng AB;
– Điểm B nối với điểm C tạo thành đoạn thẳng BC;
– Điểm C nối với điểm D tạo thành đoạn thẳng CD.
Vậy các đoạn thẳng có trong hình trên là: AB, BC, CD.
2. Độ dài đoạn thẳng
Cách đo độ dài đoạn thẳng AB:
Cho đoạn thẳng AB. Đặt cạnh của thước đi qua hai điểm A và B sao cho điểm A trùng với vạch số 0 của thước và nhìn xem điểm B trùng với vạch chỉ số bao nhiêu.
Giả sử điểm B trùng với vạch số 9 (như hình vẽ).
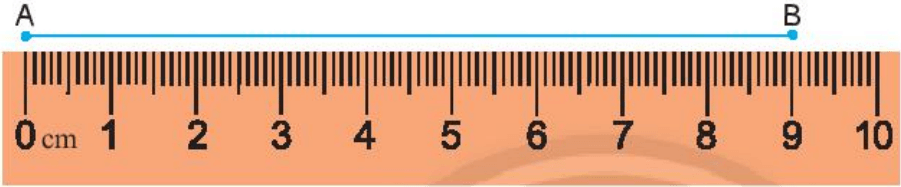
Khi đó, ta nói đoạn thẳng AB có độ dài là 9 cm.
Kí hiệu AB = 9 cm hoặc BA = 9 cm.
Việc đo độ dài đoạn thẳng được thực hiện trên cơ sở so sánh nó với đoạn thẳng được chọn làm đơn vị đo hay đoạn thẳng đơn vị.
Ví dụ 1. Cho hình vẽ dưới đây.
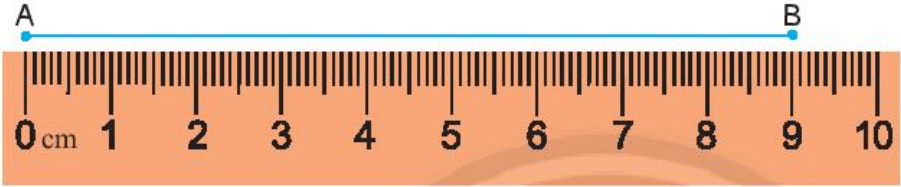
Trong hình vẽ trên, đoạn thẳng AB được tính bằng đơn vị xăng-ti-mét (cm), độ dài đoạn thẳng AB bằng 9 lần đoạn thẳng đơn vị có độ dài 1 cm.
Nhận xét:
– Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.
– Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B.
– Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.
Ví dụ 2. Cho hình vẽ dưới đây. Hỏi khoảng cách giữa hai điểm M và N là bao nhiêu?
Lời giải:
Trong hình vẽ trên cạnh của thước đi qua hai điểm M và N sao cho điểm M trùng với vạch số 0 và điểm N trùng với vạch số 5 của thước.
Do đó độ dài đoạn thẳng MN là 5 cm.
Vậy khoảng cách giữa hai điểm M và N là 5 cm.
Số đo độ dài của một đoạn thẳng không phải bao giờ cũng là số tự nhiên.
Ví dụ 3. Cho hình vẽ dưới đây.
Trong hình vẽ trên, đoạn thẳng AB = 7,5 cm (độ dài đoạn thẳng AB là một số thập phân).
3. So sánh hai đoạn thẳng
Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.
Ví dụ 4. Độ dài các đoạn thẳng: AB = 3 cm, CD = 3 cm, EF = 5 cm (như hình vẽ).
Ta nói rằng:
– Đoạn thẳng AB bằng đoạn thẳng CD và viết là AB = CD.
– Đoạn thẳng EF dài hơn đoạn thẳng AB và viết là EF > AB.
– Đoạn thẳng CD ngắn hơn đoạn thẳng EF và viết là CD < EF.
B. Bài tập tự luyện
Bài 1. Kể tên các đoạn thẳng có trong hình dưới đây:
Lời giải:
Cứ hai điểm bất kỳ được nối với nhau sẽ tạo thành một đoạn thẳng.
Ta có các cách chọn sau: (A, B); (A, C); (A, D); (B, C); (B, D); (C, D).
Trong mỗi cách chọn, cứ hai điểm sẽ tạo thành một đoạn thẳng.
Vậy các đoạn thẳng có trong hình trên là: AB, AC, AD, BC, BD, CD.
Bài 2. Cho hai điểm M và N cách nhau một khoảng bằng 9 cm. Nếu ta chọn một đoạn thẳng có độ dài 3 cm làm đơn vị độ dài thì đoạn MN có độ dài bằng bao nhiêu đơn vị vừa chọn?
Lời giải:
Hai điểm M và N cách nhau một khoảng bằng 9 cm hay độ dài đoạn thẳng MN = 9 cm.
Gọi đoạn thẳng đơn vị có độ dài 3 cm là đoạn thẳng AB.
Khi đó, AB = 3 cm.
Ta có hình vẽ:
Ta có: 9 = 3 . 3 nên MN = 3 . AB.
Do đó độ dài đoạn thẳng MN có độ dài bằng 3 lần độ dài đoạn thẳng AB.
Vậy nếu ta chọn một đoạn thẳng có độ dài 3 cm làm đơn vị độ dài thì đoạn MN bằng 3 đơn vị độ dài đoạn thẳng có độ dài 3 cm.
Bài 3. Cho đoạn thẳng OA = 8 cm. Xác định vị trí của điểm B (bằng cách vẽ hình) nằm cách A một khoảng bằng 2 cm trên đường thẳng OA trong mỗi trường hợp sau:
a) Hai điểm O và B nằm cùng phía đối với điểm A;
b) Hai điểm O và B nằm khác phía đối với điểm A.
Lời giải:
Điểm B nằm cách A một khoảng bằng 2 cm hay độ dài AB = 2 cm.
a) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm cùng phía đối với điểm A.
Nên điểm B nằm giữa hai điểm O và A.
* Cách xác định điểm B:
– Vẽ đoạn thẳng OA = 8 cm;
– Trên đoạn thẳng OA lấy điểm B sao cho AB = 2 cm.
Ta có hình vẽ:
b) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm khác phía đối với điểm A.
Nên điểm A nằm giữa hai điểm O và B.
* Cách xác định điểm B:
– Vẽ đoạn thẳng OA = 8 cm;
– Trên tia đối của tia AO, lấy điểm B sao cho AB = 2 cm.
Ta có hình vẽ:
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Lý thuyết Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Lý thuyết Bài 5: Trung điểm của đoạn thẳng
Lý thuyết Bài 6: Góc
Lý thuyết Bài 7: Số đo góc. Các góc đặc biệt
- Sách bài tập Toán 6 Bài 4 (Chân trời sáng tạo): Đoạn thẳng. Độ dài đoạn thẳng
Giải SBT Toán lớp 6 Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Bài 1 trang 93 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ hình tương ứng trong mỗi trường hợp sau:
a) đoạn thẳng AB;
b) đường thẳng AB;
c) Tia AB;
d) Tia BA.
Lời giải:
a) Cách vẽ đoạn thẳng AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, ta được đoạn thẳng AB.
Ta có hình vẽ:
b) Cách vẽ đường thẳng AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, kéo dài về hai phía, ta được đường thẳng AB.
Ta có hình vẽ:
c) Cách vẽ tia AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, kéo dài qua điểm B, ta được tia AB.
Ta có hình vẽ:
d) Cách vẽ tia BA:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm B với điểm A, kéo dài qua điểm A, ta được tia BA.
Ta có hình vẽ:
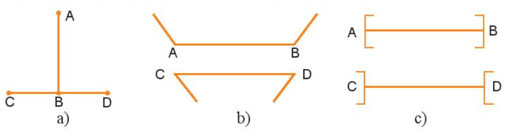
Bài 2 trang 93 sách bài tập Toán lớp 6 Tập 2: Hãy ước lượng để so sánh độ dài các đoạn thẳng AB và CD trong các hình dưới đây, sau đó dùng thước đo để kiểm tra lại.
Lời giải:
Ước lượng bằng mắt sau đó kiểm tra lại bằng thước.
Hình a)
– Ước lượng bằng mắt, dự đoán: CD > AB.
– Dùng thước đo kiểm tra được: CD > AB.
Hình b)
– Ước lượng bằng mắt bằng cách dóng thẳng điểm điểm A với điểm C, điểm B với điểm D (như hình vẽ). Dự đoán: AB = CD.
– Dùng thước đo kiểm tra được: AB = CD.
Hình c)
– Ước lượng bằng mắt bằng cách dóng thẳng điểm điểm A với điểm C, điểm B với điểm D (như hình vẽ). Dự đoán: AB = CD.
– Dùng thước đo kiểm tra được: AB = CD.
Bài 3 trang 93 sách bài tập Toán lớp 6 Tập 2: Điểm M nằm giữa hai điểm C và D. Tính độ dài đoạn thẳng CD, nếu:
a) CM = 2,5 cm và MD = 3,5 cm;
b) CM = 3,1 dm và MD = 4,6 dm;
c) CM = 12,3 m và MD = 5,8 m.
Lời giải:
Vì điểm M nằm giữa hai điểm C và D nên CD = CM + MD. Vì vậy ta có:
a) Thay CM = 2,5 cm và MD = 3,5 cm, ta được:
CD = CM + MD = 2,5 + 3,5 = 6 (cm);
Vậy CD = 6 cm.
b) Thay CM = 3,1 dm và MD = 4,6 dm, ta được:
CD = CM + MD = 3,1 + 4,6 = 7,7 (dm);
Vậy CD = 7,7 dm.
c) Thay CM = 12,3 m và MD = 5,8 m, ta được:
CD = CM + MD = 12,3 + 5,8 = 18,1 (m)
Vậy CD = 18,1 m.
Bài 4 trang 94 sách bài tập Toán lớp 6 Tập 2: Các điểm A, B, C nằm trên một đường thẳng. Biết rằng, AB = 4,3 cm, AC = 7,5 cm, BC = 3,2 cm. Trong ba điểm A, B, C điểm nào nằm giữa hai điểm còn lại?
Lời giải:
Ta có: AB + BC = 4,3 + 3,2 = 7,5 (cm).
Mà AC = 7,5 cm.
Nên: AB + BC = AC.
Vậy trong ba điểm A, B, C điểm B nằm giữa A và C.
Bài 5 trang 94 sách bài tập Toán lớp 6 Tập 2: Ba điểm A, B, C có cùng nằm trên một đường thẳng sao cho AB = 1,8 m, AC = 1,3 m, BC = 3m hay không? Hãy giải thích câu trả lời.
Lời giải:
Nếu AB + BC = AC thì điểm B nằm giữa A và C, đồng thời suy ra ba điểm này thẳng hàng.
Trong ba điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại.
Vì giả sử điểm A nằm giữa hai điểm B và C, khi đó: AB + AC = BC.
Nhưng 1, 8 + 1,3 = 3,1 > 3 (m) hay AB + AC > BC nên vô lý.
Do đó điểm A không thể nằm giữa hai điểm B và C.
Tương tự: Vì 3 > 1,8 > 1,3 hay BC > AB > CA.
Nên: BC + CA > AB và BC + AB > AC.
Do đó điểm C không nằm giữa hai điểm A và B, đồng thời điểm B cũng không nằm giữa hai điểm A và C.
Vậy ba điểm A, B và C không cùng nằm trên một đường thẳng.
Bài 6 trang 94 sách bài tập Toán lớp 6 Tập 2: Trong hình vẽ bên các đoạn thẳng ME và NF bằng nhau. Hỏi các đoạn thẳng MF và NE có bằng nhau hay không? Vì sao?
Lời giải:
Ta có: MF = ME + EF; NE = FN + EF.
Vì đoạn thẳng ME và NF bằng nhau hay ME = NF
Nên ME + EF = FN + EF.
Do đó MF = NE.
Vậy MF = NE.
Bài 7 trang 94 sách bài tập Toán lớp 6 Tập 2: Có hay không ba điểm A, B, C nằm trên một đường thẳng sao cho độ dài của đoạn thẳng AB bằng tổng độ dài của các đoạn thẳng AC và BC. Hãy vẽ hình trong trường hợp đó (nếu có).
Lời giải:
Đoạn thẳng AB bằng tổng độ dài các đoạn thẳng AC và BC.
Hay AC + BC = AB.
Do đó điểm C nằm giữa A và B, đồng thời ba điểm này thẳng hàng.
Ta có hình vẽ minh hoạ như sau:
Bài 8 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên tia AB lấy điểm C. Tìm độ dài đoạn thẳng BC nếu:
a) AB = 1,5 m và AC = 0,3 m;
b) AB = 2 cm và AC = 4,4 cm.
Lời giải:
a) Trên tia AB, vì AB > AC (1,5 m > 0,3 m) nên điểm C nằm giữa A và B. Do đó: AC + BC = AB.
Suy ra BC = AB – AC = 1,5 – 0,3 = 1,2 (m).
Vậy BC = 1,2 m.
b) Trên tia AB, vì AB < AC (2 cm < 4,4 cm) nên điểm B nằm giữa A và C.
Do đó: AB + BC = AC.
Suy ra BC = AC – AB = 4,4 – 2 = 2,2 (cm).
Vậy BC = 2,2 cm.
Bài 9 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên đoạn thẳng AB có độ dài 15 cm lấy một điểm C. Tìm độ dài của đoạn thẳng AC và BC nếu:
a) Đoạn thẳng AC ngắn hơn đoạn thẳng BC 3 cm;
b) Đoạn thẳng AC dài gấp hai lần đoạn thẳng BC;
c) Độ dài các đoạn thẳng AC và BC có tỉ lệ là 2 : 3.
Lời giải:
Vì điểm C nằm trên đoạn thẳng AB nên điểm C nằm giữa A và B.
Nên AC + BC = AB = 15 (cm).
a) Đoạn thẳng AC ngắn hơn đoạn thẳng BC 3 cm hay AC + 3 = BC.
Do đó AC + BC = AC + AC + 3 = 15
2AC = 15 – 3
2AC = 12
AC = 6 (cm)
Suy ra: BC = AC + 3 = 6 + 3 = 9 (cm).
Vậy AC = 6 cm, BC = 9 cm.
b) Đoạn thẳng AC dài gấp hai lần đoạn thẳng BC hay AC = 2BC.
Do đó AC + BC = 2BC + BC = 3BC = 15.
Suy ra BC = 15 : 3 = 5 (cm); AC = 2BC = 2 . 5 = 10 (cm).
Vậy BC = 5 cm, AC = 10 cm.
c) Độ dài các đoạn thẳng AC và BC có tỉ lệ là 2 : 3 hay AC : BC = 2 : 3.
Suy ra AC =
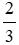BC.Do đó AC + BC =
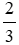BC + BC = BC( 
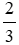+ 1) = 
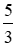BC = 15.Suy ra BC 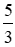= 15 :
= 15.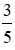 
= 9 (cm); AC = 
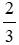BC =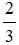 
. 9 = 6 (cm).Vậy BC = 9 cm, AC = 6 cm.
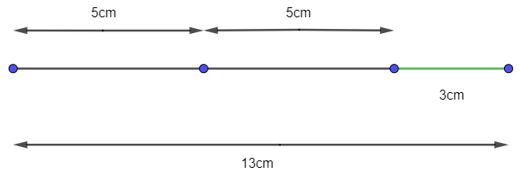
Bài 10 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên thang chia của thước bị mờ chỉ còn các điểm chia 0 cm; 5 cm và 13 cm. Có thể chỉ sử dụng chiếc thước này để vẽ các đoạn thẳng có độ dài lần lượt dưới đây hay không?
a) 3 cm;
b) 2 cm;
c) 1 cm.
Lời giải:
Dựa vào mối liên hệ giữa các số 5; 13 với lần lượt các số 1; 2; 3, ta có thể vẽ được các đoạn thẳng này.
a) Vì 3 cm = 13 cm – 5 cm – 5cm, nên ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 13 cm.
+ Giữ thước trên đoạn thẳng đó, đánh dấu liên tiếp hai đoạn thẳng có độ dài 5 cm.
Đoạn thẳng còn lại sẽ dài 3 cm.
Ta có hình vẽ:
b) Vì 2 cm = 5 cm – 3 cm, ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 5 cm.
+ Giữ thước trên đoạn thẳng đó, đánh dấu đoạn thẳng có độ dài 3 cm (dựa vào câu a).
Đoạn thẳng còn lại sẽ dài 2 cm.
Ta có hình vẽ:
c) Vì 1 cm = 3 cm – 2 cm, ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 3 cm (dựa vào câu a).
+ Giữ thước trên đoạn thẳng đó, đánh dấu đoạn thẳng có độ dài 2 cm (dựa vào câu b).
Đoạn thẳng còn lại sẽ dài 1 cm.
Ta có hình vẽ:
Bài 11 trang 94 sách bài tập Toán lớp 6 Tập 2: Xác định khoảng cách giữa Thủ đô Hà Nội và Thành phố Hồ Chí Minh bằng bản đồ.
Hướng dẫn: Để tính khoảng cách trên thực tế giữa hai địa điểm bằng cách sử dụng bản đồ, ta đo khoảng cách giữa hai vị trí đó trên bản đồ rồi sử dụng tỉ lệ bản đồ. Chẳng hạn, nếu ta đo được khoảng cách giữa hai địa điểm ở trên bản đồ là 12 cm, tỉ lệ bản đồ là 1 : 1 000 000, thì khoảng cách trên thực tế của hai địa điểm đó là 12 000 000 cm hay 12 km.
Lời giải:
Chẳng hạn: Ta sử dụng bản đồ tỉ lệ 1 : 10 000 000, tức là 1 cm trên bản đồ tương ứng khoảng cách trên thực tế là 10 000 000 cm hay 100 km.
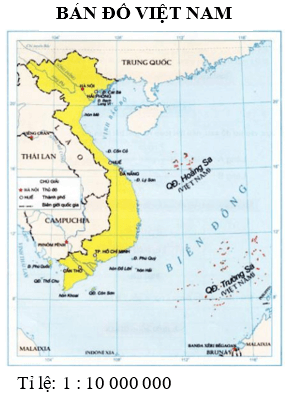
Ta đo được khoảng cách giữa Thủ đô Hà Nội và thành phố Hồ Chí Minh trên bản đồ xấp xỉ 8,5 cm.
Vậy khoảng cách thực tế giữa Thủ đô Hà Nội và thành phố Hồ Chí Minh xấp xỉ là: 8,5 . 100 = 850 (km).
- Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng (Kết nối tri thức 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 34: Đoạn thẳng. Độ dài đoạn thẳng
Video giải Toán 6 Bài 34: Đoạn thẳng. Độ dài đoạn thẳng – Kết nối tri thức
I. Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng
1. Đoạn thẳng
– Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.
– A; B là hai đầu mút (mút) của đoạn thẳng AB.
Ví dụ 1: Đọc tên các đoạn thẳng có trong hình:
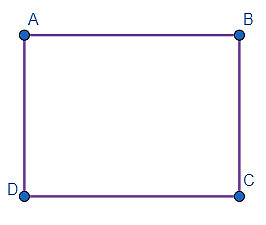
Các đoạn thẳng có trong hình là: AB; BC; CD; DA.
2. Độ dài đoạn thẳng
a) Độ dài đoạn thẳng
– Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).
– Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).
– Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…
Ví dụ 2: Quan sát hình vẽ
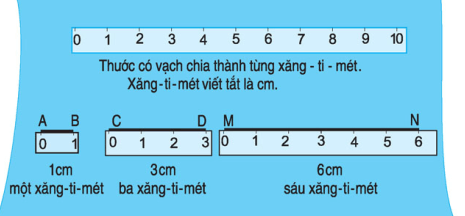
Ta thấy:
+ Độ dài đoạn thẳng AB là 1cm.
+ Độ dài đoạn thẳng CD là 3cm.
+ Độ dài đoạn thẳng MN là 6cm.
b) So sánh độ dài đoạn thẳng
– Hai đoạn thẳng AB và EG có cùng độ dài. Ta viết AB = EG và nói đoạn thẳng AB bằng đoạn thẳng EG.
– Đoạn thẳng AB có độ dài nhỏ nhơn đoạn thẳng CD. Ta viết AB < CD và nói AB ngắn hơn CD hoặc CD > AB và nói CD dài hơn AB.
c) Đo độ dài đoạn thẳng
Để đo độ dài đoạn thẳng ta làm như sau:
Bước 1: Đặt thước trùng với đường thẳng sao cho vạch 0 của thước trùng với một đầu mút của đoạn thẳng.
Bước 2: Quan sát xem đầu mút còn lại trùng với vạch mấy của thước thì số chỉ ở vạch đó chính là độ dài đoạn thẳng.
Chú ý: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB
II. Bài tập vận dụng
Bài 1: Kể tên các đoạn thẳng có trong hình
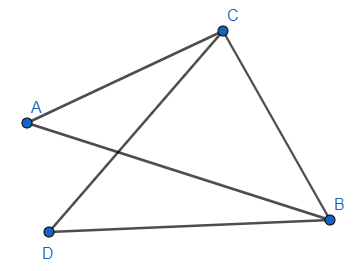
Lời giải:
Các đoạn thẳng có trong hình là AB; AC; BC; BD; CD.
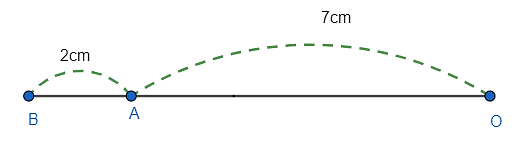
Bài 2: Có đoạn thẳng OA = 7cm. Xác định vị trí của điểm B (bằng cách vẽ hình) nằm cách A một khoảng 2cm trên đường thẳng OA trong mỗi trường hợp sau:
a) Hai điểm O và B nằm cùng phía đối với điểm A;
b) Hai điểm O và B nằm khác phía đối với điểm A.
Lời giải:
a) Hai điểm O và B nằm cùng phía đối với điểm A
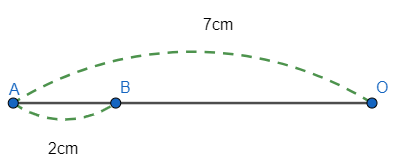
b) Hai điểm O và B nằm khác phía đối với điểm A
Bài 3: Cho M và N là hai điểm cùng nằm giữa điểm E và F. Tính độ dài của đoạn thẳng MN, biết rằng EF = 12cm; EM = 4cm và NF = 5cm.
Lời giải:
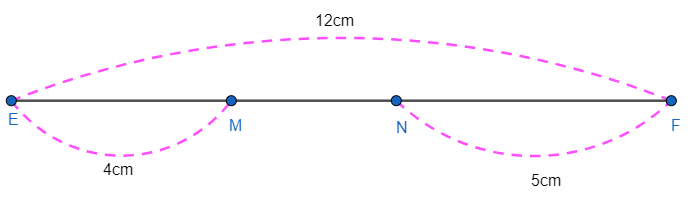
Điểm N nằm giữa điểm E và điểm F nên
EN + NF = EF
Thay số: EN + 5 = 12
EN = 12 – 5
EN = 7cm
Lại có M nằm giữa E và N nên
EM + MN = EN
Thay số: 4 + MN = 7
MN = 7 – 4
MN = 3cm
Vậy MN = 3cm
Bài giảng Toán 6 Bài 34: Đoạn thẳng. Độ dài đoạn thẳng – Kết nối tri thức
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 33: Điểm nằm giữa hai điểm. Tia
Lý thuyết Bài 34: Đoạn thẳng. Độ dài đoạn thẳng
Lý thuyết Bài 35: Trung điểm của đoạn thẳng
Lý thuyết Bài 36: Góc
Lý thuyết Bài 37: Số đo góc
- Sách bài tập Toán 6 Bài 34 (Kết nối tri thức): Đoạn thẳng. Độ dài đoạn thẳng
Giải SBT Toán lớp 6 Bài 34: Đoạn thẳng. Độ dài đoạn thẳng
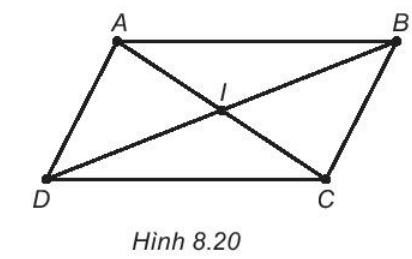
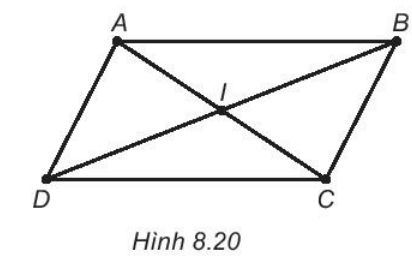
Bài 8.26 trang 49 sách bài tập Toán lớp 6 Tập 2: Xem Hình 8.20.
Dùng compa để kiểm tra sự bằng nhau của hai đoạn thẳng trong mỗi cặp: AB và CD; AD và BC.
Lời giải:
Lời giải:
* Kiểm tra sự bằng nhau của AB và CD:
– Đặt tâm của compa vào một đầu mút của đoạn thẳng AB, đầu bút của compa chạm vào mút còn lại.
– Giữ khoảng cách giữ tâm và đầu bút.
– Tiếp tục đặt tâm của compa vào một đầu mút của đoạn thẳng CD. Kiểm tra xem đầu bút của compa có chạm vào mút còn lại hay không.
Ta thấy: đầu bút của compa chạm vào mút còn lại nên AB = CD.
* Kiểm tra sự bằng nhau của AD và BC:
– Đặt tâm của compa vào một đầu mút của đoạn thẳng AD, đầu bút của compa chạm vào mút còn lại.
– Giữ khoảng cách giữ tâm và đầu bút.
– Tiếp tục đặt tâm của compa vào một đầu mút của đoạn thẳng BC. Kiểm tra xem đầu bút của compa có chạm vào mút còn lại hay không.
Ta thấy: đầu bút của compa chạm vào mút còn lại nên AD = BC.
Bài 8.27 trang 49 sách bài tập Toán lớp 6 Tập 2: Dùng thước để đo độ dài của các đoạn thẳng IA, IB, IC và ID (đơn vị milimét). Em có nhận xét gì về độ dài các đoạn thẳng đã đo?
Lời giải:
* Đo độ dài cạnh IA:
Đặt thước sao cho mép thước dọc theo cạnh IA. Một trong hai điểm I và A trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm A trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IA.
Do đó, độ dài đoạn thẳng IA = 18 mm.
* Đo độ dài cạnh IB:
Đặt thước sao cho mép thước dọc theo cạnh IB. Một trong hai điểm I và B trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm B trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IB.
Do đó, độ dài đoạn thẳng IB = 27 mm.
* Đo độ dài cạnh IC:
Đặt thước sao cho mép thước dọc theo cạnh IC. Một trong hai điểm I và C trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm C trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IC.
Do đó, độ dài đoạn thẳng IC = 18 mm.
* Đo độ dài cạnh ID:
Đặt thước sao cho mép thước dọc theo cạnh ID. Một trong hai điểm I và D trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm D trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng ID.
Do đó, độ dài đoạn thẳng ID = 27 mm.
Vậy IA = IC = 18 mm; IB = ID = 27 mm.
Bài 8.28 trang 49 sách bài tập Toán lớp 6 Tập 2: Cho hai điểm A và B cách nhau một khoảng bằng 8 cm. Nếu ta chọn một đoạn thẳng có độ dài 2 cm làm đơn vị độ dài thì đoạn AB có độ dài bằng bao nhiêu đơn vị vừa chọn?
Lời giải:
Hai điểm A và B cách nhau một khoảng bằng 8 cm hay độ dài đoạn thẳng AB = 8 cm.
Gọi đoạn thẳng đơn vị có độ dài 2 cm là đoạn thẳng MN.
Khi đó, MN = 2 cm.
Ta có hình vẽ:
Ta có: 8 = 4 . 2 nên AB = 4 . MN.
Do đó độ dài đoạn thẳng AB có độ dài bằng 4 lần độ dài đoạn thẳng MN.
Vậy nếu ta chọn một đoạn thẳng có độ dài 2 cm làm đơn vị độ dài thì đoạn AB bằng 4 đơn vị độ dài đoạn thẳng có độ dài 2 cm.
Bài 8.29 trang 49 sách bài tập Toán lớp 6 Tập 2: Cho đoạn thẳng OA = 7 cm. Xác định vị trí của điểm B (bằng cách vẽ hình) nằm cách A một khoảng bằng 3 cm trên đường thẳng OA trong mỗi trường hợp sau:
a) Hai điểm O và B nằm cùng phía đối với điểm A;
b) Hai điểm O và B nằm khác phía đối với điểm A.
Lời giải:
Điểm B nằm cách A một khoảng bằng 3 cm hay độ dài AB = 3 cm.
a) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm cùng phía đối với điểm A.
Nên điểm B nằm giữa hai điểm O và A.
* Cách xác định điểm B:
– Vẽ đoạn thẳng OA = 7 cm;
– Trên đoạn thẳng OA lấy điểm B sao cho AB = 3 cm.
Ta có hình vẽ:
b) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm khác phía đối với điểm A.
Nên điểm A nằm giữa hai điểm O và B.
* Cách xác định điểm B:
– Vẽ đoạn thẳng OA = 7 cm;
– Trên tia đối của tia AO, lấy điểm B sao cho AB = 3 cm.
Ta có hình vẽ:
Bài 8.30 trang 49 sách bài tập Toán lớp 6 Tập 2: Gọi S là một điểm thuộc đoạn thẳng PQ. Tính độ dài đoạn thẳng PQ nếu PS = 3 cm và SQ = 5 cm
Lời giải:
Vì S là một điểm thuộc đoạn thẳng PQ nên S nằm giữa hai điểm P và Q (như hình vẽ).
Ta có: SP + SQ = PQ
Do đó PQ = 3 + 5 = 8 (cm)
Vậy PQ = 8 cm.
Bài 8.31 trang 49 sách bài tập Toán lớp 6 Tập 2: Gọi M là một điểm thuộc đoạn thẳng EF. Hãy so sánh hai đoạn thẳng EM và MF, biết rằng EF =10 cm và MF = 5 cm.
Lời giải:
Vì M là một điểm thuộc đoạn thẳng EF nên điểm M nằm giữa hai điểm E và F (như hình vẽ).
Ta có: EM + MF = EF
EM + 5 = 10
EM = 10 – 5
EM = 5 cm.
Mà MF = 5 cm.
Vậy EM = EF.
Bài 8.32 trang 49 sách bài tập Toán lớp 6 Tập 2: Cho M và N là hai điểm cùng nằm giữa điểm E và F. Tính độ dài của đoạn thẳng MN, biết rằng EF = 12 cm, EM = 4 cm và NF = 5 cm.
Lời giải:
Ta có: EF = EM + MN + NF
12 = 4 + MN + 5
12 = 9 + MN
MN = 12 – 9
MN = 3 cm.
Vậy MN = 3 cm.
Bài 8.33 trang 49 sách bài tập Toán lớp 6 Tập 2: Bạn Nam dùng một cây gậy dài 1,5 m để đo chiều rộng của lớp học. Sau 5 lần đặt gậy đo liên tiếp thì khoảng cách còn lại giữa đầu gậy và mép tường là 1 m. Hỏi chiều rộng của lớp học là bao nhiêu mét?
Lời giải:
Cây gậy dài 1,5 m nên mỗi lần đặt gậy tương ứng với 1,5 m.
Do đó 5 lần đặt gậy tương ứng với độ dài là:
5 . 1,5 = 7,5 (m).
Chiều rộng của lớp học bằng 5 lần đặt cây gậy 1,5 m thì khoảng cách còn lại là 1 m.
Khi đó, chiều rộng của lớp học là:
7,5 + 1 = 8,5 (m).
Vậy chiều rộng của lớp học là 8,5 m.
Bài 8.34 trang 49 sách bài tập Toán lớp 6 Tập 2: Ta có nhận xét rằng trong ba điểm thẳng hàng, luôn có một điểm nằm giữa hai điểm còn lại. Giả sử A, B, C là ba điểm thẳng hàng. Nếu BC = AB + AC thì trong ba điểm đó, điểm nào nằm giữa hai điểm còn lại.
Lời giải:
Ba điểm A, B, C thẳng hàng thì có 3 trường hợp có thể xảy ra:
– Trường hợp 1: Điểm B nằm giữa hai điểm A và C.
Khi đó, AC = BA + BC.
– Trường hợp 2: Điểm C nằm giữa hai điểm A và B.
Khi đó, AB = AC + CB.
– Trường hợp 3: Điểm A nằm giữa hai điểm B và C.
Khi đó, BC = AB + AC. Đây là hệ thức đã cho.
Vậy BC = AB + AC thì trường hợp 3 xảy ra, tức là điểm A nằm giữa hai điểm B và C.
Bài 8.35 trang 49 sách bài tập Toán lớp 6 Tập 2: Giả sử A, B và C là ba điểm thẳng hàng, thỏa mãn các điều kiện AC = 2 cm; AB = 3 cm và BC = 5 cm. Vẽ hình và cho biết trong ba điểm đó, điểm nào nằm giữa hai điểm còn lại.
Lời giải:
* Cách vẽ:
– Vẽ đoạn thẳng AB = 5 cm.
– Trên đoạn thẳng AB lấy AC = 2 cm.
* Ta có hình vẽ:
Theo đề bài: AC = 2 cm; AB = 3 cm và BC = 5 cm.
Ta thấy BC = AB + AC (vì 5 = 3 + 2)
Do đó, điểm A nằm giữa hai điểm B và C.
Vậy trong ba điểm A, B, C thì điểm A nằm giữa hai điểm B và C.
- Một người đi xe đạp trên một đoạn đường thẳng từ A đến B (H.8.23).Em có nhận xét gì về những vị trí mà người đó đã đi qua so với hai điểm A và B?
Câu hỏi:
Một người đi xe đạp trên một đoạn đường thẳng từ A đến B (H.8.23).Em có nhận xét gì về những vị trí mà người đó đã đi qua so với hai điểm A và B?
Trả lời:
Mỗi vị trí mà người đó đã đi qua đều nằm giữa hai điểm A và B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====