Cho đường tròn (O) ngoại tiếp tam giác nhòn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.a) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.b) Chứng minh NB2 = NK.NMc) Chứng minh tứ giác BHIK là hình thoi.d) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.

Câu hỏi:

Cho đường tròn (O) ngoại tiếp tam giác nhòn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.a) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.b) Chứng minh ${\mathrm{NB}}^2$ = NK.NMc) Chứng minh tứ giác BHIK là hình thoi.d) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.

Trả lời:

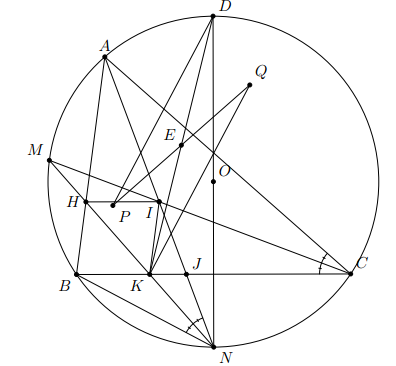
Chứng minh tương tự các ý ở trên, ta được KI // BH  (5)Từ (4) và (5) suy ra BHIK là hình bình hành.Từ (6) và (7) suy ra BH = BKMà BHIK là hình bình hành nên BHIK là hình thoi.Mà hai góc này ở vị trí đồng vị nên PK // CD => PK // DQ  (10)Chứng minh tương tự ta có C, Q, D thẳng hàng và QK // DP  (11)Từ (10) và (11) suy ra DPKQ là hình bình hành.Mà E là trung điểm của đường chéo PQ nên E cũng là trung điểm của đường chéo DK.Vậy D, E, K thẳng hàng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho đường tròn tâm O, đường kính AB = 2R. Lấy M∈O với AM < BM. Trên cạnh MB lấy điểm C sao cho MC = MA. Gọi OD là bán kính vuông góc với AB (M và D ở hai bên đường thẳng AB)a) Chứng minh AMB^=900. Tính theo R độ dài các cạnh củab) Chứng tỏ MD là phân giác AMB^=900 và MD⊥ACc) Chứng minh rằng D là tâm của đường tròn (ABC)d) Đường tròn (ABC) cắt MD tại I. Chứng minh I là tâm đường tròn nội tiếp ∆MAB
   
   

   Câu hỏi:
   

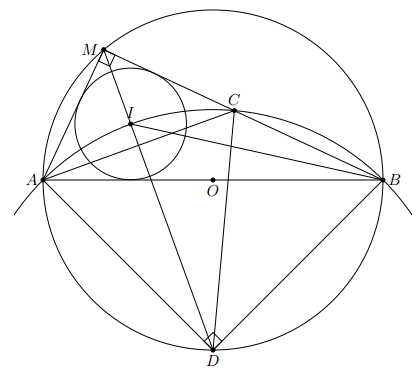
   Cho đường tròn tâm O, đường kính AB = 2R. Lấy $\mathrm{M}\in \left(\mathrm{O}\right)$ với AM < BM. Trên cạnh MB lấy điểm C sao cho MC = MA. Gọi OD là bán kính vuông góc với AB (M và D ở hai bên đường thẳng AB)a) Chứng minh $\widehat{\mathrm{AMB}}={90}^0$. Tính theo R độ dài các cạnh củab) Chứng tỏ MD là phân giác $\widehat{\mathrm{AMB}}={90}^0$ và $\mathrm{MD}\perp \mathrm{AC}$c) Chứng minh rằng D là tâm của đường tròn (ABC)d) Đường tròn (ABC) cắt MD tại I. Chứng minh I là tâm đường tròn nội tiếp $∆\mathrm{MAB}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB, AO).a) Chứng minh rằng A, B, O, C cùng thuộc một đường tròn và xác định tâm của đường tròn này.b) Chứng minh rằng AB2=AD.AEc) Gọi H là giao điểm của OA và BC. Chứng minh rằng ∆ADH~∆AEO và tứ giác DEOH nội tiếp.d) Đường thẳng AO cắt đường tròn (O) tại M, N (M nằm giữa A và O). Chứng minh rằng EHAN=MHAD
   
   

   Câu hỏi:
   

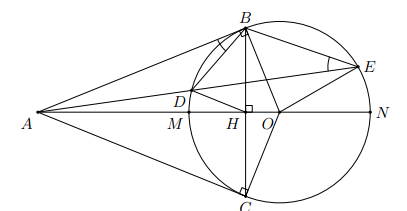
   Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB, AO).a) Chứng minh rằng A, B, O, C cùng thuộc một đường tròn và xác định tâm của đường tròn này.b) Chứng minh rằng ${\mathrm{AB}}^2=\mathrm{AD}.\mathrm{AE}$c) Gọi H là giao điểm của OA và BC. Chứng minh rằng $∆\mathrm{ADH}~∆\mathrm{AEO}$ và tứ giác DEOH nội tiếp.d) Đường thẳng AO cắt đường tròn (O) tại M, N (M nằm giữa A và O). Chứng minh rằng $\frac{\mathrm{EH}}{\mathrm{AN}}=\frac{\mathrm{MH}}{\mathrm{AD}}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E. Hai tiếp tuyến EM và Bx của (O) cắt nhau tại D (M thuộc (O))a) Chứng minh rằng 4 điểm O, M, D, B cùng thuộc một đường tròn.b) Chứng minh ∆EMA~∆EBM, suy ra EM2=EO2-R2c) Trên đoạn ME lấy điểm C sao cho hai góc CAM^, EDO^ bằng nhau. Chứng minh rằng OC // MB.d) Giả sử M là trung điểm đoạn ED. Tính EM theo R.
   
   

   Câu hỏi:
   

   Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E. Hai tiếp tuyến EM và Bx của (O) cắt nhau tại D (M thuộc (O))a) Chứng minh rằng 4 điểm O, M, D, B cùng thuộc một đường tròn.b) Chứng minh $∆\mathrm{EMA}~∆\mathrm{EBM}$, suy ra ${\mathrm{EM}}^2={\mathrm{EO}}^2–{\mathrm{R}}^2$c) Trên đoạn ME lấy điểm C sao cho hai góc $\widehat{\mathrm{CAM}}, \widehat{\mathrm{EDO}}$ bằng nhau. Chứng minh rằng OC // MB.d) Giả sử M là trung điểm đoạn ED. Tính EM theo R.

   Trả lời:

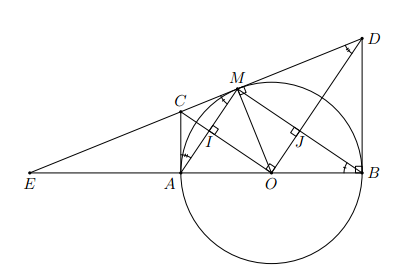   a) Vì EM và BD là tiếp tuyến với đường tròn (O) nênVậy tứ giác DMOB nội tiếp, suy ra 4 điểm O, M, D, B cùng thuộc một đường tròn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC nội tiếp đường tròn (O; R). Gọi đường tròn (I; r) đường tròn nội tiếp tam giác ABC, H là tiếp điểm của AB với đường tròn (I), D là giao điểm của AI với đường tròn (O), DK là đường kính của đường tròn (O). Gọi d là độ dài của OI. Chứng minh rằng:a) ∆AHI~∆KCDb) DI=DB=DCc) IA.ID=R2-d2d) d2=R2-2Rr
   
   

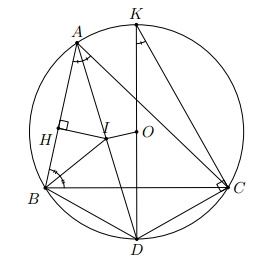
   Câu hỏi:
   

   Cho tam giác ABC nội tiếp đường tròn (O; R). Gọi đường tròn (I; r) đường tròn nội tiếp tam giác ABC, H là tiếp điểm của AB với đường tròn (I), D là giao điểm của AI với đường tròn (O), DK là đường kính của đường tròn (O). Gọi d là độ dài của OI. Chứng minh rằng:a) $∆\mathrm{AHI}~∆\mathrm{KCD}$b) $\mathrm{DI}=\mathrm{DB}=\mathrm{DC}$c) $\mathrm{IA}.\mathrm{ID}={\mathrm{R}}^2–{\mathrm{d}}^2$d) ${\mathrm{d}}^2={\mathrm{R}}^2–2\mathrm{Rr}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax của nửa đường tròn đó (Ax nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc Cax cắt nửa đường tròn tại D. kéo dài AD và BC cắt nhau tại E. kẻ EH vuông góc với Ax tại H.a) Chứng minh tứ giác AHEC nội tiếp đường tròn.b) Chứng minh ABD^=BDC^c) Chứng minh tam giác ABE cân.d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi.
   
   

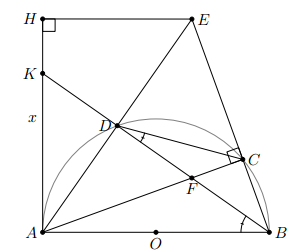
   Câu hỏi:
   

   Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax của nửa đường tròn đó (Ax nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc Cax cắt nửa đường tròn tại D. kéo dài AD và BC cắt nhau tại E. kẻ EH vuông góc với Ax tại H.a) Chứng minh tứ giác AHEC nội tiếp đường tròn.b) Chứng minh $\widehat{\mathrm{ABD}}=\widehat{\mathrm{BDC}}$c) Chứng minh tam giác ABE cân.d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====