Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z1 ; z2 ; z3 .Biết | z1| = | z2| = | z3| và z1+ z2= 0 . Khi đó tam giác ABC là tam giác gì?

Câu hỏi:

Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z₁ ; z₂ ; z₃ .Biết | z₁| = | z₂| = | z₃| và z₁+ z₂= 0 . Khi đó tam giác ABC là tam giác gì?

A. Tam giác ABC đều.

B. Tam giác ABC vuông tại C.

Đáp án chính xác

C. Tam giác ABC cân tại C.

D. Tam giác ABC vuông cân tại C.

Trả lời:

Chọn B.
Vì  z₁+ z₂= 0  nên z₁ ; z₂ là hai số phức đối nhau, do đó hai điểm A: B đối xứng qua gốc O ( tức O là trung điểm của đoạn thẳng AB).
Lại có | z₁| = | z₂| = | z₃|
Vậy tam giác ABC có độ dài đường trung tuyến bằng một nửa cạnh huyền nên vuông tại C.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z  thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
   
   

   Câu hỏi:
   

   Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z  thỏa mãn điều kiện |z – 2| + |z + 2| = 10.

   A. Đường tròn ( x – 2) ² + ( y + 2) ² = 100.

   B. Elip 

   C. Đường tròn  ( x -2) ² + ( y + 2) ² = 10.

   D. Elip 

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Gọi M(x; y)  là điểm biểu diễn số phức z = x + yi, x, y ∈ R
   Gọi A là điểm biểu diễn số phức 2
   Gọi B là điểm biểu diễn số phức -2
   Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
   Ta có AB = 4.
   Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0)  tiêu cự  AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
   Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho số phức z  thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z  là?
   
   

   Câu hỏi:
   

   Cho số phức z  thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z  là?

   

   Đáp án chính xác

   

   C. ( x + 2) ² + ( y – 2) ² = 64.

   D. ( x + 2) ² + ( y – 2) ² = 8.

   Trả lời:

   Chọn A.
    
   Gọi M(x; y) , F₁= ( -2; 0) và F₂( 2; 0).
   Ta có |z + 2| + |z – 2| = 8 
   $\iff \sqrt{{\left(x+2\right)}^2+y^2}+\sqrt{{\left(x–2\right)}^2+y^2}=8$
   Hay MF₁+ MF₂ = 8.
   Do đó điểm M(x; y)  nằm trên elip (E ) có 2a = 8 nên a = 4
   ta có F₁F₂ = 2c nên 4 = 2c  hay c = 2
   Ta có b² = a² – c² = 16 – 4 = 12
   Vậy tập hợp các điểm M là elip 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm nghiệm của phương trình:
   
   

   Câu hỏi:
   

   Tìm nghiệm của phương trình:

   

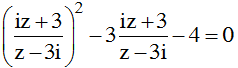
   B.  Không có z thỏa mãn

   Đáp án chính xác

   

   

   Trả lời:

   Chọn B.
   Điều kiện: z $\ne$ 3i
   Đặt . Phương trình đã cho trở thành: t² – 3t – 4 = 0
   Suy ra: t = 4 hoặc t = -1
   Với t = 4 thì 
   Hay iz + 3 = 4( z – 3i)
   $\iff \left(–4+i\right)z=–12i–3\iff z= \frac{–12i–3}{–4+i}=3i$
   Không thỏa mãn.
   Với t = -1 thì 
   Suy ra: iz + 3 =  -1 ( z – 3i)
   ( 1 + i) z = -3 + 3i hay z = 3i (không thỏa mãn)
   Vậy không có z thỏa mãn.
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm nghiệm của phương trình: ( z + 3 – i)2 – 6( z + 3 – i) + 13 = 0
   
   

   Câu hỏi:
   

   Tìm nghiệm của phương trình: ( z + 3 – i)² – 6( z + 3 – i) + 13 = 0

   A. z = 3i; z = 1 – 2i

   B. z = – i; z = 3i + 4

   C. z = 3i + 4; z = 3i

   D. z = 3i; z = -i

   Đáp án chính xác

   Trả lời:

   Chọn  D.
   Đặt t = z + 3 – i. Phương trình đã cho trở thành: t² – 6t + 13 = 0
   Suy ra :  t = 3 + 2i hoặc t = 3 – 2i
   Với t = 3+ 2i thì z + 3 – i = 3 + 2i hay z = 3i
   Với t = 3- 2i thì z + 3 – i = 3 -2i hay z = – i

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm nghịch đảo của số phức z, biết z thỏa mãn | z – 2i| =|z¯ + 2 + 4i| và z-iz¯+ i  là số thuần ảo.
   
   

   Câu hỏi:
   

   Tìm nghịch đảo của số phức z, biết z thỏa mãn | z – 2i| =|$\overline{z}$ + 2 + 4i| và $\frac{z–i}{\overline{z}+ i }$ là số thuần ảo.

   

   

   

   Đáp án chính xác

   

   Trả lời:

   Chọn C.
   Giả sử z = a+ bi thì  khi và chỉ khi a = b – 4  (1)
   Với a ≠ 0  hoặc b ≠ 1, ta có:
   
   Vì  là số thuần ảo nên a² – ( b – 1) ² = 0 khi và chỉ khi a = b – 1 hoặc a = 1 – b
   Kết hợp (1)  ta có a = -3/2 và b = 5/2.
   Nên số phức đó là
   Vậy $\frac{1}{z}=–\frac{3}{17}–\frac{5}{17}i$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====