Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trỉnh chính tắc là x2a2+y2b2=1, trong đó a > b > 0 (Hình 2). a) Tìm toạ độ hai tiêu điểm F1, F2 của (E). b) (E) cắt trục Ox tại các điểm A1, A2 và cắt trục Oy tại các điểm B1, B2. Tìm độ dài các đoạn thẳng OA2 và OB2.

Câu hỏi:

Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trỉnh chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, trong đó a > b > 0 (Hình 2).

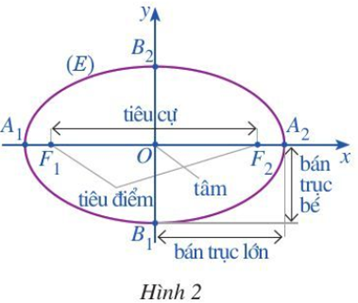
a) Tìm toạ độ hai tiêu điểm F₁, F₂ của (E).
b) (E) cắt trục Ox tại các điểm A₁, A₂ và cắt trục Oy tại các điểm B₁, B₂. Tìm độ dài các đoạn thẳng OA₂ và OB₂.

Trả lời:

a) Toạ độ hai tiêu điểm F₁, F₂ của (E) là F₁ $\left(-\sqrt{a^2-b^2};0\right),$ F₂ $\left(\sqrt{a^2-b^2};0\right).$
b)
+) Vì A₂ thuộc trục Ox nên toạ độ của A₂ có dạng $\left(x_{A_2};0\right).$
Mà A₂ thuộc (E) nên $\frac{x_{{}_{A_2}}^2}{a^2}+\frac{0^2}{b^2}=1\Rightarrow x_{{}_{A_2}}^2=a^2\Rightarrow \left[\begin{array}{l}{x}_{A_2}=a\\ x_{A_2}=-a\end{array}\right..$
Ta thấy A₂ nằm bên phải điểm O trên trục Ox nên  $x_{A_2}>0\Rightarrow x_{A_2}=a$ $\Rightarrow$ A₂(a; 0). Khi đó OA₂ = $\sqrt{{\left(a-0\right)}^2+{\left(0-0\right)}^2}=\sqrt{a^2}=a$(vì a > 0).
Vậy OA₂ = a.
+) Vì B₂ thuộc trục Oy nên toạ độ của B₂ có dạng $\left(0;y_{B_2}\right).$
Mà B₂ thuộc (E) nên $\frac{0^2}{a^2}+\frac{y_{{}_{B_2}}^2}{b^2}=1\Rightarrow y_{{}_{B_2}}^2=b^2\Rightarrow \left[\begin{array}{l}{y}_{B_2}=b\\ y_{B_2}=-b\end{array}\right..$
Ta thấy B₂ nằm bên trên điểm O trên trục Oy nên $y_{B_2}>0\Rightarrow y_{B_2}=b\Rightarrow$ B₂(0; b). Khi đó OB₂ = $\sqrt{{\left(0-0\right)}^2+{\left(b-0\right)}^2}=\sqrt{b^2}=b$ (vì b > 0).
Vậy OB₂ = b.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho elip có phương trình chính tắc x2a2+y2b2=1 (H.3.1). a) Tìm toạ độ các giao điểm của elip với các trục toạ độ. b) Hãy giải thích vì sao, nếu điểm M(x0; y0) thuộc elip thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc elip. c) Với điểm M(x0; y0) thuộc elip, hãy so sánh OM2 với a2, b2.
   
   

   Câu hỏi:
   

   Cho elip có phương trình chính tắc $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (H.3.1).
   
   a) Tìm toạ độ các giao điểm của elip với các trục toạ độ.
   b) Hãy giải thích vì sao, nếu điểm M(x₀; y₀) thuộc elip thì các điểm có toạ độ (x₀; –y₀), (–x₀; y₀), (–x₀; –y₀) cũng thuộc elip.
   c) Với điểm M(x₀; y₀) thuộc elip, hãy so sánh OM² với a², b².

   Trả lời:

   
   
   

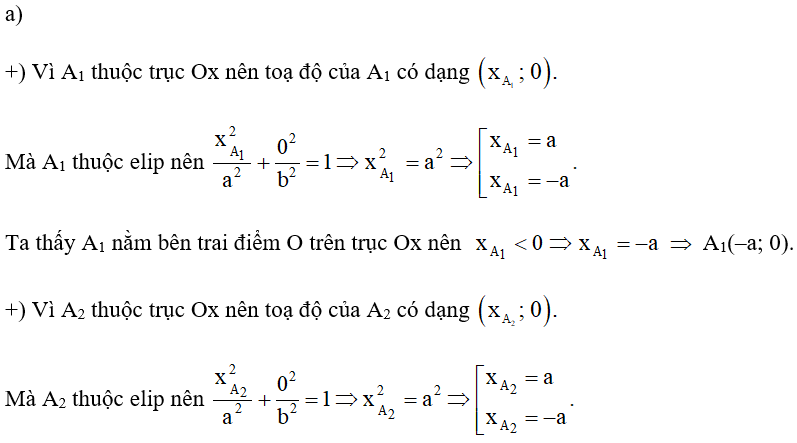
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.

   Trả lời:

   Gọi phương trình chính tắc của elip đã cho là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).
   Theo đề bài ta có:
   – Độ dài trục lớn bằng 10, suy ra 2a = 10, suy ra a = 5.
   – Elip có một tiêu cự bằng 6, suy ra 2c = 6 hay c = 3, suy ra b2 = a2 – c2 = 52 – 32 = 16.
   Vậy phương trình chính tắc của elip đã cho là $\frac{x^2}{25}+\frac{y^2}{16}=1.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. (Phép co đường tròn) Cho đường tròn có phuong trình x2 + y2 = a2 và số k (0 < k < 1). Với mỗi điểm M(x0; y0) thuộc đường tròn, gọi H(x0; 0) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho HN = kHM (H.3.5). a) Tính toạ độ của N theo x0; y0; k. b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên elip có phương trình chính tắc x2a2+y2(ka)2=1.
   
   

   Câu hỏi:
   

   (Phép co đường tròn) Cho đường tròn có phuong trình x² + y² = a² và số $k$ (0 < k < 1). Với mỗi điểm M(x₀; y₀) thuộc đường tròn, gọi H(x₀; 0) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho HN = kHM (H.3.5).
   a) Tính toạ độ của N theo x₀; y₀; k.
   b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên elip có phương trình chính tắc $\frac{x^2}{a^2}+\frac{y^2}{{\left(ka\right)}^2}=1$.

   Trả lời:

   a) Gọi toạ độ của N là (x_N; y_N­). Khi đó $\overrightarrow{HN}=\left(x_N-x_0;y_N-0\right)=\left(x_N-x_0;y_N\right).$
   Vì HN = kHM nên $\overrightarrow{HN}=k\overrightarrow{HM}.$ Mà $\overrightarrow{HM}=\left(x_0-x_0;y_0-0\right)=\left(0;y_0\right)$ nên $\left\{\begin{array}{l}{x}_N-x_0=k.0\\ y_N=k.y_0\end{array}\right.\Rightarrow \left\{\begin{array}{l}{x}_N=x_0\\ y_N=k{y}_0\end{array}\right..$
   b) Khi M thay đổi trên đường tròn ta luôn có $x_0^2+y_0^2=a^2.$
   Do đó $\frac{x_N^2}{a^2}+\frac{y_N^2}{{\left(ka\right)}^2}=\frac{x_0^2}{a^2}+\frac{{\left(k{y}_0\right)}^2}{{\left(ka\right)}^2}=\frac{x_0^2}{a^2}+\frac{y_0^2}{a^2}=\frac{x_0^2+y_0^2}{a^2}=\frac{a^2}{a^2}=1.$
   Vậy N luôn thay đổi trên elip có phương trình chính tắc $\frac{x^2}{a^2}+\frac{y^2}{{\left(ka\right)}^2}=1$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho elip có hai tiêu điểm F1(–c; 0), F2(c; 0) và độ dài trục lớn bằng 2a và điểm M(x; y). a) Tính MF12 – MF22. b) Khi điểm M thuộc elip (MF1 + MF2 = 2a), tính MF1 – MF2, MF1, MF2.
   
   

   Câu hỏi:
   

   Cho elip có hai tiêu điểm F₁(–c; 0), F₂(c; 0) và độ dài trục lớn bằng 2a và điểm M(x; y).
   a) Tính MF₁² – MF₂².
   b) Khi điểm M thuộc elip (MF₁ + MF₂ = 2a), tính MF₁ – MF₂, MF₁, MF₂.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho elip x236+y220=1, điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Cho elip $\frac{x^2}{36}+\frac{y^2}{20}=1$, điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?

   Trả lời:

   Có a² = 36, suy ra a = 6.
   $c=\sqrt{a^2-b^2}=\sqrt{36-20}=\sqrt{16}=4.$
   Gọi toạ độ của M là (x; y).
   Ta xét khoảng cách từ M đến F₁.
   Theo công thức độ dài bán kính qua tiêu ta có MF₁ = 6 + $\frac{4}{6}$x = 6 + $\frac{2}{3}$x.
   Mặt khác, vì M thuộc elip nên –6 ≤ x ≤ 6
    $\Rightarrow -\frac{2}{3}.6\le \frac{2}{3}x\le \frac{2}{3}.6\Rightarrow -4\le \frac{2}{3}x\le 4\Rightarrow 2\le 6+\frac{2}{3}x\le 10.$
   Vậy 2 ≤ MF₁ ≤ 10.
   Vậy độ dài MF₁ nhỏ nhất bằng 2 khi M có hoành độ bằng –6, lớn nhất bằng 10 khi M có hoành độ bằng 6.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====