Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức MF12 – MF22 = 4cx và |MF1 – MF2| = 2a, chứng minh: MF1=a+cax= |a+ex|;  MF2=a−cax= |a−ex|.

Câu hỏi:

Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức MF₁² – MF₂² = 4cx và |MF₁ – MF₂| = 2a, chứng minh:
$M{F}_1=\left|a+\frac{c}{a}x\right|=|a+ex|;M{F}_2=\left|a-\frac{c}{a}x\right|=|a-ex|.$

Trả lời:

+) Nếu điểm M thuộc nhánh bên phải trục Oy thì MF₁ > MF₂. Khi đó:
MF₁ – MF₂ = |MF₁ – MF₂| = 2a.
Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)2a = 4cx
$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = $\frac{2c}{a}$x. Khi đó:
(MF₁ + MF₂) + (MF₁ – MF₂) = $\frac{2c}{a}x$ + 2a $\Rightarrow$ 2MF₁ = $\frac{2c}{a}x$ + 2a
$\Rightarrow$ MF₁ = a + $\frac{c}{a}$x $=\left|a+\frac{c}{a}x\right|=|a+ex|.$
(MF₁ + MF₂) – (MF₁ – MF₂) = $\frac{2c}{a}x$ – 2a $\Rightarrow$2MF₂ = $\frac{2c}{a}x$ – 2a
$\Rightarrow$ MF₂ = $\frac{c}{a}$ x – a =  $=\left|a-\frac{c}{a}x\right|=|a-ex|.$

+) Nếu điểm M thuộc nhánh bên phải trái Oy thì MF₁ < MF₂. Khi đó:
MF₁ – MF₂ = –|MF₁ – MF₂| = –2a.
Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)(–2a) = 4cx
$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = – $\frac{2c}{a}x$. Khi đó:
(MF₁ + MF₂) + (MF₁ – MF₂) = – + (–2a) $\Rightarrow$ 2MF₁ = – $\frac{2c}{a}x$ – 2a
 
$\Rightarrow$ MF₁ = $-\left(\frac{c}{a}x+a\right)=\left|a+\frac{c}{a}x\right|=|a+ex|.$
(MF₁ + MF₂) – (MF₁ – MF₂) = – $\frac{2c}{a}x$ – (–2a) $\Rightarrow$ 2MF₂ = – $\frac{2c}{a}x$ + 2a
$\Rightarrow$ MF₂ =  a –$\frac{c}{a}$x $=\left|a-\frac{c}{a}x\right|=|a-ex|.$
Vậy trong cả hai trường hợp ta đều có
$M{F}_1=\left|a+\frac{c}{a}x\right|=|a+ex|;M{F}_2=\left|a-\frac{c}{a}x\right|=|a-ex|.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là x2a2−y2b2=1, trong đó a > 0, b > 0 (Hình 13). a) Tìm toạ độ hai tiêu điểm F1, F2 của hypebol (H). b) Hypebol (H) cắt trục Ox tại các điểm A1, A2. Tìm độ dài các đoạn thẳng OA1 và OA2.
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó a > 0, b > 0 (Hình 13).
   

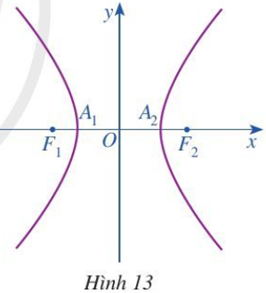
   a) Tìm toạ độ hai tiêu điểm F₁, F₂ của hypebol (H).
   b) Hypebol (H) cắt trục Ox tại các điểm A₁, A₂. Tìm độ dài các đoạn thẳng OA₁ và OA₂.

   Trả lời:

   a) Toạ độ hai tiêu điểm F₁, F₂ của hypebol (H) là: F₁(–c; 0) và F₂(c; 0) với $c=\sqrt{a^2+b^2}.$
   b)
   +) Vì A₁ thuộc trục Ox nên toạ độ của A₁ có dạng $\left(x_{A_1};0\right).$
   Mà A₁ thuộc (H) nên $\frac{x_{{}_{A_1}}^2}{a^2}+\frac{0^2}{b^2}=1\Rightarrow x_{{}_{A_1}}^2=a^2\Rightarrow \left[\begin{array}{l}{x}_{A_1}=a\\ x_{A_1}=-a\end{array}\right..$
   Ta thấy A₁ nằm bên trái điểm O trên trục Ox nên $x_{A_1}<0\Rightarrow x_{A_1}=-a\Rightarrow$A₁(–a; 0). Khi đó OA₁ = $\sqrt{{\left(-a-0\right)}^2+{\left(0-0\right)}^2}=\sqrt{{\left(-a\right)}^2}=a$(vì a > 0).
   Vậy OA₁ = a.
   +) Vì A₂ thuộc trục Ox nên toạ độ của A₂ có dạng $\left(x_{A_2};0\right).$
   Mà A₂ thuộc (H) nên $\frac{x_{{}_{A_2}}^2}{a^2}+\frac{0^2}{b^2}=1\Rightarrow x_{{}_{A_2}}^2=a^2\Rightarrow \left[\begin{array}{l}{x}_{A_2}=a\\ x_{A_2}=-a\end{array}\right..$
   Ta thấy A₂ nằm bên phải điểm O trên trục Ox nên $x_{A_2}>0\Rightarrow x_{A_2}=a\Rightarrow$A₂(a; 0). Khi đó OA₂ = $\sqrt{{\left(a-0\right)}^2+{\left(0-0\right)}^2}=\sqrt{a^2}=a$(vì a > 0).
   Vậy OA₂ = a.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là x2a2−y2b2=1, trong đó a > 0, b > 0 (Hình 14). Cho điểm M(x; y) nằm trên hypebol (H). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Các điểm M1, M2, M3 có nằm trên hypebol (H) hay không? Tại sao?
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó a > 0, b > 0 (Hình 14).
   

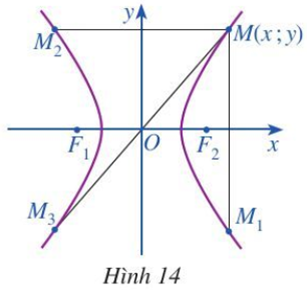
   Cho điểm M(x; y) nằm trên hypebol (H). Gọi M₁, M₂, M₃ lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Các điểm M₁, M₂, M₃ có nằm trên hypebol (H) hay không? Tại sao?

   Trả lời:

   Theo đề bài, M(x; y) nằm trên (H) nên ta có: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$
   +) M₁ là điểm đối xứng của M qua trục Ox, suy ra M₁ có toạ độ là (x; –y).
   Ta có $\frac{x^2}{a^2}-\frac{{\left(-y\right)}^2}{b^2}=\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$ Do đó M₁ cũng thuộc (H).
   +) M₂ là điểm đối xứng của M qua trục Oy, suy ra M₂ có toạ độ là (–x; y).
   Ta có $\frac{{\left(-x\right)}^2}{a^2}-\frac{y^2}{b^2}=\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$ Do đó M₂ cũng thuộc (H).
   +) M₃ là điểm đối xứng của M qua gốc O, suy ra M₃ có toạ độ là (–x; –y).
   Ta có $\frac{{\left(-x\right)}^2}{a^2}-\frac{{\left(-y\right)}^2}{b^2}=\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$ Do đó M₃ cũng thuộc (H).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và chứng tỏ rằng x ≤ –a hoặc x ≥ a. b) Viết phương trình hai đường thẳng PR và QS.
   
   

   Câu hỏi:
   

   a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và chứng tỏ rằng x ≤ –a hoặc x ≥ a.
   b) Viết phương trình hai đường thẳng PR và QS.
   

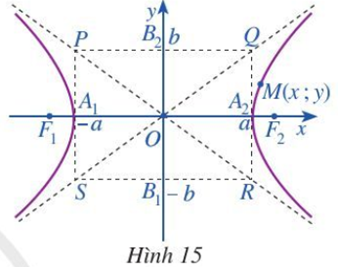
   Trả lời:

   a) Nếu điểm M(x; y) thuộc (H) thì $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$
   Vì $\frac{y^2}{b^2}\ge 0$ nên $\frac{x^2}{a^2}\ge 1\Rightarrow x^2\ge a^2\Rightarrow$ x ≤ –a hoặc x ≥ a.
   b)
   +) Có P(–a; b), R(a; –b) $\Rightarrow \overrightarrow{PR}=\left(a-\left(-a\right);-b-b\right)=\left(2a;-2b\right).$
   Do đó ta chọn (b; a) là một vectơ pháp tuyến của PR.
   Khi đó phương trình đường thẳng PR là: b(x + a) + a(y – b) = 0 hay bx + ay = 0 hay $y=-\frac{b}{a}x.$
   +) Có Q(a; b), S(–a; –b) $\Rightarrow \overrightarrow{QS}=\left(-a-a;-b-b\right)=\left(-2a;-2b\right).$
   Do đó ta chọn (–b; a) là một vectơ pháp tuyến của QS.
   Khi đó phương trình đường thẳng QS là: –b(x – a) + a(y – b) = 0 hay –bx + ay = 0 hay $y=\frac{b}{a}x.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm cận là y = –3x.
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của hypebol có một đỉnh là A₂(5; 0) và một đường tiệm cận là y = –3x.

   Trả lời:

   Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).
   +) Hypebol có một đỉnh là A₂(5; 0) $\Rightarrow$ a = 5.
   +) Hypebol có một đường tiệm cận là y = –3x $\Rightarrow \frac{b}{a}=3\Rightarrow$b = 3a = 15.
   Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{5^2}-\frac{y^2}{{15}^2}=1$ hay $\frac{x^2}{25}-\frac{y^2}{225}=1.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Nêu định nghĩa tâm sai của elip có phương trình chính tắc là x2a2+y2b2=1 với a > b > 0.
   
   

   Câu hỏi:
   

   Nêu định nghĩa tâm sai của elip có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với a > b > 0.

   Trả lời:

   Tâm sai e của elip có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với a > b > 0 là tỉ số giữa tiêu cự và độ dài trục lớn của elip, tức là $e=\frac{c}{a}=\frac{\sqrt{a^2-b^2}}{a}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====