Câu hỏi:
Cho hai bất phương trình 2x + y < 3 (1) và – x + 3y > 5 (2) và điểm A(0; 1). Kết luận nào sau đây là đúng?
A. Điểm A thuộc miền nghiệm của bất phương trình (1) và (2);
B. Điểm A thuộc miền nghiệm của bất phương trình (1) nhưng không thuộc miền nghiệm của (2);
Đáp án chính xác
C. Điểm A không thuộc miền nghiệm của bất phương trình (1) nhưng thuộc miền nghiệm của (2);
D. Điểm A không thuộc miền nghiệm của cả hai bất phương trình (1) và (2).
Trả lời:
Đáp án đúng là: B
Với cặp số (x; y) = (0; 1)
Vì 2.0 + 1 = 1 < 3 nên cặp số (0; 1) là nghiệm của bất phương trình 2x + y < 3 (1).
Do đó điểm A(0; 1) thuộc miền nghiệm của bất phương trình (1).
Vì –0 + 3.1 = 3 < 5 nên cặp số (0; 1) không phải là nghiệm của bất phương trình – x + 3y > 5 (2).
Do đó điểm A(0; 1) không thuộc miền nghiệm của bất phương trình (2).
Vậy điểm A(0 ; 1) thuộc miền nghiệm của bất phương trình (1) nhưng không thuộc miền nghiệm của (2).
Vậy ta chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bạn Lan để dành được 300 nghìn đồng. Trong một đợt ủng hộ học sinh khó khăn, bạn Lan đã ủng hộ x tờ tiền loại 10 nghìn đồng, y tờ tiền loại 20 nghìn đồng từ tiền để dành của mình. Trong các bất phương trình sau, bất phương trình nào diễn tả giới hạn về tổng số tiền mà bạn Lan đã ủng hộ.
Câu hỏi:
Bạn Lan để dành được 300 nghìn đồng. Trong một đợt ủng hộ học sinh khó khăn, bạn Lan đã ủng hộ x tờ tiền loại 10 nghìn đồng, y tờ tiền loại 20 nghìn đồng từ tiền để dành của mình. Trong các bất phương trình sau, bất phương trình nào diễn tả giới hạn về tổng số tiền mà bạn Lan đã ủng hộ.
A. x + y < 300 ;>
B. 10x + y < 300 ;>
C. 10x + 20y > 300;
D. 10x + 20y ≤ 300.
Đáp án chính xác
Trả lời:
Đáp án đúng là: DSố tiền mệnh giá 10 nghìn đồng là: 10x (nghìn đồng)Số tiền mệnh giá 20 nghìn đồng là: 20y (nghìn đồng) Tổng số tiền bạn Lan đã ủng hộ là: 10x + 20y (nghìn đồng).Vì tổng số tiền Lan ủng hộ không vượt quá số tiền Lan để dành được là 300 nghìn đồng nên ta có bất phương trình: 10x + 20y ≤ 300.Vậy ta chọn đáp án D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Câu hỏi:
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x2 < 3x – 7y;>
B. x + 3y2 ≥0;
C. –22x + y ≤4;
Đáp án chính xác
D. 0x – 0y ≤ 5.
Trả lời:
Đáp án đúng là: Cx2 < 3x – 7y và x + 3y2> ≥ 0 là bất phương trình hai ẩn bậc hai; 0x – 0y ≤ 5 có hệ số của x và y đồng thời bằng 0. Vì vậy, A, B, D không phải là bất phương trình bậc nhất hai ẩn.Ta có: –22x + y ≤ 4 ⇔ –4x + y ≤ 4.Vì –4x + y ≤ 4 có dạng bất phương trình bậc nhất hai ẩn với a = –4; b = 1; c = 4 nên đáp án C đúng.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bất phương trình nào tương đương với bất phương trình 3x – y > 7(x – 4y) + 1?
Câu hỏi:
Bất phương trình nào tương đương với bất phương trình 3x – y > 7(x – 4y) + 1?
A. 4x – 27y + 1 > 0;
B. 4x – 27y + 1 ≥ 0;
C. 4x – 27y < –1;>
Đáp án chính xác
D. 4x – 27y + 1 ≤ 0.
Trả lời:
Đáp án đúng là: CTa có : 3x – y > 7(x – 4y) + 1 ⇔ 3x – y > 7x – 28y + 1 ⇔ 0 > 7x – 3x – 28y + y + 1 ⇔ 4x – 27y + 1 < 0 ⇔ 4x – 27y < –1.Vậy ta chọn phương án C.>>
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Câu hỏi:
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x2 + y > 0;
B. x2 + 3y2 = 2;
C. –x + y3 ≤ 0;
D. x – y < 1.>
Đáp án chính xác
Trả lời:
Đáp án đúng là: Dx2 + y > 0 là bất phương trình bậc hai. Do đó đáp án A sai.x2 + 3y2 = 2 là phương trình bậc hai. Do đó đáp án B sai.–x + y3 ≤ 0 là bất phương trình bậc ba. Do đó đáp án C sai.x – y < 1 có dạng bất phương trình bậc nhất hai ẩn (ẩn x và ẩn y) với: a = 1; b = –1; c = 1. Do đó đáp án D đúng.>
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giá trị nhỏ nhất Fmin của biểu thức F= –x + y trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{ – 2x + y \ge 2}\\{y – x \le 4}\\{x + 2y \ge 5}\end{array}} \right.\) là:
Câu hỏi:
Giá trị nhỏ nhất Fmin của biểu thức F= –x + y trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{ – 2x + y \ge 2}\\{y – x \le 4}\\{x + 2y \ge 5}\end{array}} \right.\) là:
A. Fmin = \(\frac{{11}}{5}\);
Đáp án chính xác
B. Fmin = 0;
C. Fmin = 2;
D. Fmin = 4.
Trả lời:
Đáp án đúng là: A \(\left\{ {\begin{array}{*{20}{c}}{ – 2x + y \ge 2}\\{y – x \le 4}\\{x + 2y \ge 5}\end{array}} \right.\)Ta biểu diễn miền nghiệm của hệ đã cho trên mặt phẳng tọa độ, ta được hình ảnh sau:
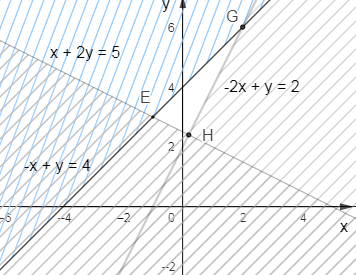Khi đó miền tam giác EGH (bao gồm cả biên) là miền nghiệm của hệ bất phương trình đã cho.Các đỉnh E, H, G có tọa độ: E(–1; 3); H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)); G(2; 6).Ta tính giá trị của F = –x + y tại các đỉnh của tam giác EGH.Tại E(–1; 3) ta có F = –(–1) + 3 = 4;Tại H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)) ta có F = – \(\frac{1}{5}\)+\(\frac{{12}}{5}\)= \(\frac{{11}}{5}\);Tại G(2; 6) ta có F = –2 + 6 = 4.Suy ra F nhỏ nhất bằng \(\frac{{11}}{5}\) tại H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)), tức là Fmin = \(\frac{{11}}{5}\).Ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====