Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.

Câu hỏi:

Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.

A. \(\sqrt {43} \);

Đáp án chính xác

B. \(2\sqrt {13} \);

C. 8;

D. \(8\sqrt 3 \).

Trả lời:

Đáp án đúng là: A

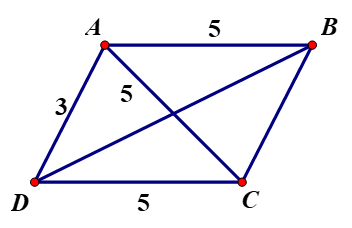
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: \(\cos \alpha = \frac{{{3^2} + {5^2} – {5^2}}}{{2.3.5}} = \frac{3}{{10}}\)
⇒ α là góc nhọn
⇒\(\alpha = \widehat {ADC}\)
⇒ AC = 5
⇒\(B{D^2} = A{D^2} + A{B^2} – 2.AD.AB.\cos \widehat {BAD} = A{D^2} + A{B^2} + 2.AD.AB.\cos \widehat {ADC}\)
(vì \(\widehat {BAD}\) và \(\widehat {ADC}\) bù nhau\( \Rightarrow \cos \widehat {BAD} = – \cos \widehat {ADC}\))
⇒ BD² = 3² + 5² + 2.3.5.\(\frac{3}{{10}}\) = 43
⇒ BD = \(\sqrt {43} \).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
   
   

   Câu hỏi:
   

   Tam giác ABC có A = 120° khẳng định nào sau đây đúng?

   A. a² = b² + c² – 3bc;

   B. a² = b² + c² + bc;

   Đáp án chính xác

   C. a² = b² + c² + 3bc;

   D. a² = b² + c² – bc.

   Trả lời:

   Đáp án đúng là: B
   Áp dụng định lí Côsin tại đỉnh A ta có: a² = b² + c² – 2bc.cosA
   \( \Rightarrow \)a² = b² + c² – 2bc.cos120° = b² + c² + bc.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Giá trị của tan(180°) bằng
   
   

   Câu hỏi:
   

   Giá trị của tan(180°) bằng

   A. 1;

   B. 0;

   Đáp án chính xác

   C. – 1;

   D. Không xác định.

   Trả lời:

   Đáp án đúng là: B
   Ta có tan(180°) = \(\frac{{\sin (180^\circ )}}{{\cos (180^\circ )}} = \frac{0}{{ – 1}} = 0\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho 0° < α < 90°. Kết luận nào sau đây đúng
   
   

   Câu hỏi:
   

   Cho 0° < α < 90°. Kết luận nào sau đây đúng

   A. tan(α) > 0; cot(α) > 0;

   B. tan(α) < 0; cot(α) < 0;

   Đáp án chính xác

   C. tan(α) > 0; cot(α) < 0;

   D. tan(α) < 0; cot(α) > 0.

   Trả lời:

   Đáp án đúng là: B
   Vì 0° < α < 90° (Góc phần tư thứ 1) nên tan(α) > 0; cot(α) > 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trong các đẳng thức sau, đẳng thức nào đúng?
   
   

   Câu hỏi:
   

   Trong các đẳng thức sau, đẳng thức nào đúng?

   A. sin(180° – α) = – cos α;

   B. sin(180° – α) = – sin α;

   C. sin(180° – α) = sin α;

   Đáp án chính xác

   D. sin(180° – α) = cos α.

   Trả lời:

   Đáp án đúng là: C
   Đối với 2 góc bù nhau α và 180° – α ta có
   sin(180° – α) = sin α; cos(180° – α) = – cos α;
   tan(180° – α) = – tan α (α ≠ 90°); cot(180° – α) = – cot α (0 < α < 180°);

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho \(\cos \alpha = – \frac{4}{5}\) và góc α thỏa mãn 90° < α < 180°. Khi đó.
   
   

   Câu hỏi:
   

   Cho \(\cos \alpha = – \frac{4}{5}\) và góc α thỏa mãn 90° < α < 180°. Khi đó.

   A. \(\cot \alpha = \frac{4}{3}\);

   B. \(\sin \alpha = \frac{3}{5}\);

   Đáp án chính xác

   C. \(\tan \alpha = \frac{4}{5}\).

   D. \(\sin \alpha = – \frac{3}{5}\).

   Trả lời:

   Đáp án đúng là: B
   Ta có sin²α + cos²α = 1
   ⇔ sin²α = 1 – cos²α = 1 – \({\left( { – \frac{4}{5}} \right)^2}\)= 1 – \(\frac{{16}}{{25}}\)= \(\frac{9}{{25}}.\)
   ⇔ \(\left[ \begin{array}{l}\sin \alpha = \frac{3}{5}\\\sin \alpha = – \frac{3}{5}\end{array} \right.\)
   Vì 90° < α < 180° nên sinα > 0. Do đó \(\sin \alpha = \frac{3}{5}\)
   ⇒ tanα = \(\frac{{\sin \alpha }}{{cos\alpha }} = – \frac{3}{4}\), cotα = \(\frac{{co{\mathop{\rm s}\nolimits} \alpha }}{{\sin \alpha }} = – \frac{4}{3}\).
   Vậy đáp án đúng là B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====