Câu hỏi:
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?
A. \(2\overrightarrow a + \overrightarrow b \) và \(\frac{1}{3}\overrightarrow a – \frac{1}{2}\overrightarrow b \);
B. \( – \overrightarrow a + \overrightarrow b \) và \( – 2\overrightarrow a + 3\overrightarrow b \);
C. \(\frac{1}{6}\overrightarrow a – \overrightarrow b \) và \( – \overrightarrow a + 6\overrightarrow b \);
Đáp án chính xác
D. \(\overrightarrow a + \overrightarrow b \) và \(\overrightarrow a – \overrightarrow b \).
Trả lời:
Đáp án đúng là C
Ta có: \( – 6\left( {\frac{1}{6}\overrightarrow a – \overrightarrow b } \right) = – \overrightarrow a + \overrightarrow b \). Do đó vectơ \(\frac{1}{6}\overrightarrow a – \overrightarrow b \) và \( – \overrightarrow a + 6\overrightarrow b \) cùng phương.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \) với số thực k như thế nào thì vectơ \(k\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow a \).
Câu hỏi:
Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \) với số thực k như thế nào thì vectơ \(k\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow a \).
A. k = 1;
B. k = 0;
C. k < 0;
Đáp án chính xác
D. k > 0.
Trả lời:
Đáp án đúng là C
Tích của một vectơ \(\overrightarrow a \ne \overrightarrow 0 \)với số thực k < 0 là một vec tơ kí hiệu \(k\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow a \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho vectơ \(\overrightarrow a \), \(\overrightarrow b \) và hai số thực k, t. Khẳng định nào sau đây là sai?
Câu hỏi:
Cho vectơ \(\overrightarrow a \), \(\overrightarrow b \) và hai số thực k, t. Khẳng định nào sau đây là sai?
A. k(t\(\overrightarrow a \)) = (kt)\(\overrightarrow a \);
B. (k + t)\(\overrightarrow a \) = k\(\overrightarrow a \) + t\(\overrightarrow b \);
Đáp án chính xác
C. k\(\left( {\overrightarrow a + \overrightarrow b } \right)\) = k\(\overrightarrow a \) + k\(\overrightarrow b \);
D. (-1)\(\overrightarrow a \) = -\(\overrightarrow a \).
Trả lời:
Đáp án đúng là B
Ta có (k + t)\(\overrightarrow a \) = k\(\overrightarrow a \) + t\(\overrightarrow a \). Do đó B sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \).Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
Câu hỏi:
Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \).Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
A. k < 0
B. k = 1
C. 0 < k < 1
D. k > 1
Đáp án chính xác
Trả lời:
Đáp án đúng là D
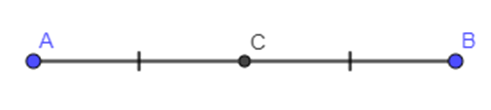
Vì C là trung điểm của đoạn thẳng AB nên AC = 2AB.
Ta có \(\overrightarrow {AC} ,\overrightarrow {AB} \) là hai vectơ cùng hướng nên \(\overrightarrow {AC} = 2\overrightarrow {AB} \). Suy ra k = 2 > 1.
Vậy k thỏa mãn điều kiện k > 1.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
Câu hỏi:
Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
A. K là trung điểm của AB
B. K là điểm nằm giữa I và A thỏa mãn IK = \(\frac{1}{3}\) IB với I là trung điểm của AB.
C. K là điểm nằm giữa I và B thỏa mãn IK = \(\frac{1}{3}\) IB với I là trung điểm của AB.
Đáp án chính xác
D. K là điểm nằm giữa I và A thỏa mãn IK = \(\frac{1}{3}\) IA với I là trung điểm của AB.
Trả lời:
Đáp án đúng là C
Gọi I là trung điểm của đoạn thẳng AB. Khi đó \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
Xét đẳng thức: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {KI} + \overrightarrow {IA} + 2\left( {\overrightarrow {KI} + \overrightarrow {IB} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 3\overrightarrow {KI} + \overrightarrow {IA} + 2\overrightarrow {IB} = \overrightarrow 0 \)
\( \Leftrightarrow 3\overrightarrow {KI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + \overrightarrow {IB} = \overrightarrow 0 \)
\( \Leftrightarrow 3\overrightarrow {KI} + \overrightarrow 0 + \overrightarrow {IB} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {KI} = – \frac{1}{3}\overrightarrow {IB} \) hay \(\overrightarrow {IK} = \frac{1}{3}\overrightarrow {IB} \)
Vì vậy điểm K là điểm nằm giữa I và B thỏa mãn \(IK = \frac{1}{3}IB\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có đường trung tuyến AM. Khi đó \(\overrightarrow {AM} = a\overrightarrow {AB} + b\overrightarrow {AC} \). Tính S = a + 2b.
Câu hỏi:
Cho tam giác ABC có đường trung tuyến AM. Khi đó \(\overrightarrow {AM} = a\overrightarrow {AB} + b\overrightarrow {AC} \). Tính S = a + 2b.
A. 1;
B. 2;
C. \(\frac{1}{2}\);
D. \(\frac{3}{2}.\)
Đáp án chính xác
Trả lời:
Đáp án đúng là D
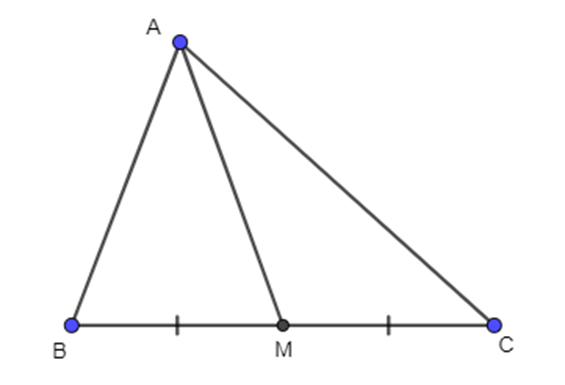
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
⇔ \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
⇒ a = \(\frac{1}{2}\), b = \(\frac{1}{2}\).
⇒ S = a + 2b = \(\frac{1}{2}\) + 2.\(\frac{1}{2}\) = \(\frac{1}{2}\) + 1 = \(\frac{3}{2}\).
Vậy S = \(\frac{3}{2}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====