Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp

Câu hỏi:

Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp

A. 1

B. 2

C. 3

Đáp án chính xác

D. 4

Trả lời:

Đáp án CĐường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp của tam giácVới một tam giác có ba đường tròn bàng tiếp

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tâm đường tròn nội tiếp của tam giác là 
   
   

   Câu hỏi:
   

   Tâm đường tròn nội tiếp của tam giác là 

   A. giao của ba đường phân giác góc trong tam giác

   Đáp án chính xác

   B. giao ba đường trung trực của tam giác

   C. trọng tâm tam giác

   D. trực tâm của tam giác

   Trả lời:

   Đáp án ATâm đường tròn nội tiếp của tam giác là giao của ba đường phân giác góc trong tam giác

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai? 
   
   

   Câu hỏi:
   

   Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai? 

   A. Khoảng cách từ điểm đó đến hai tiếp điểm là bằng nhau

   B. Tia nối từ hai tiếp điểm là tia phân giác của góc tạo bởi bán kính và đường tiếp tuyến

   Đáp án chính xác

   C. Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính

   D. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai tiếp tuyến

   Trả lời:

   Đáp án BNếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:+ Điểm đó cách đều hai tiếp điểm+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Vẽ đường kính CD của (O). Khi đó:
   
   

   Câu hỏi:
   

   Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Vẽ đường kính CD của (O). Khi đó:

   A. BD // OA

   Đáp án chính xác

   B. BD // AC

   C. BD ⊥ OA

   D. BD cắt OA

   Trả lời:

   Đáp án A
   
   *Xét tam giác BOC có OB = OC = R nên tam giác OBC cân tại O có OH là đường phân giác của góc  ( tính chất hai tiếp tuyến cắt nhau).
   Do đó, OH đồng thời là đường cao: 
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai? 
   
   

   Câu hỏi:
   

   Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai? 

   A. AC + BD = CD

   B. AC . BD = $R^2$

   C. $O{D}^2$ = DB. (AC + DB)

   D. Có 2 khẳng định sai

   Đáp án chính xác

   Trả lời:

   Đáp án D
   
   * Do AC và CI là 2 tiếp tuyến cắt nhau tại C nên: CA = CI ( tính chất 2 tiếp tuyến cắt nhau)
   * Do BD và DI là 2 tiếp tuyến cắt nhau tại D nên: DB = DI ( tính chất 2 tiếp tuyến cắt nhau).
   Suy ra: AC + BD = CI + DI = CD. – A đúng
   +) AC.BD = CI.DI (1)
   Xét tam giác COD vuông tại O có đường cao OI nên:
   CI.ID = $I{O}^2$ = $R^2$ (2) 
   Từ (1) và (2) suy ra: AC.BD = $R^2$     – B đúng
   Và $O{D}^2$ = DI.DC = DB . (AC + BD) – C đúng
   Vậy không có khẳng định nào là sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho đường tròn (O; 6cm) . Gọi A là điểm nằm ngoài đường tròn sao cho OA = 10cm.Qua A dựng hai tiếp tuyến AM và AN đến (O), với M và N là tiếp điểm. Gọi giao điểm của AO và MN là H. Tìm khẳng định đúng?
   
   

   Câu hỏi:
   

   Cho đường tròn (O; 6cm) . Gọi A là điểm nằm ngoài đường tròn sao cho OA = 10cm.Qua A dựng hai tiếp tuyến AM và AN đến (O), với M và N là tiếp điểm. Gọi giao điểm của AO và MN là H. Tìm khẳng định đúng?

   A. OH = 3,6cm

   Đáp án chính xác

   B. AH = 4,8cm

   C. MH = 6,4 cm

   D.Tất cả sai

   Trả lời:

   Đáp án A
   
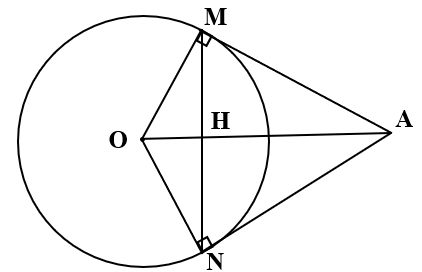
   Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là đường phân giác của góc MON
   Tam giác MON có OM = ON (= R) nên đây là tam giác cân tại O có OH là đường phân giác nên đồng thời là đường cao.
   Xét tam giác AMO vuông tại M có MH là đường cao.Áp dụng hệ thức cạnh và góc trong tam giác vuông ta có:
   
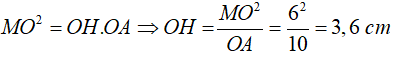
   +) AH = AO – OH = 10 – 3,6 = 6,4 cm
   +) $M{H}^2$ = OH.AH = 3,6.6,4 = 23,04 ⇒ MH = 4,8cm

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====