Tập nghiệm của bất phương trình 2×2 – 7x – 15 ≥ 0 là:

Câu hỏi:

Tập nghiệm của bất phương trình 2x² – 7x – 15 ≥ 0 là:

A.\(\left( {–\infty ; – \frac{3}{2}} \right] \cup [5; + \infty )\);

Đáp án chính xác

B.\(\left[ { – \frac{3}{2};5} \right]\);

C.\(\left( {–\infty ; – 5} \right] \cup \left[ {\frac{3}{2}; + \infty } \right)\);

D.\(\left[ { – 5;\frac{3}{2}} \right]\).

Trả lời:

Đáp án đúng là: A
Xét tam thức f(x) = 2x² – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = \( – \frac{3}{2}\) và a = 2 > 0.
Ta có bảng xét dấu :

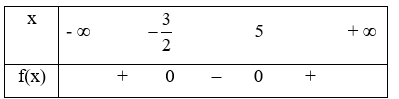
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là \(\left( {–\infty ; – \frac{3}{2}}

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tập nghiệm của bất phương trình x2 + 4x + 4 > 0 là:
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình x² + 4x + 4 > 0 là:

   A. (– 2; + ∞) ;

   B. (– ∞; – 2);

   C. (– ∞; – 2)\( \cup \)(– 2; + ∞) ;

   Đáp án chính xác

   D. (– ∞; + ∞)

   Trả lời:

   Đáp án đúng là: C
   Tam thức bậc hai f(x) = x² + 4x + 4 có ∆ = 0; nghiệm là x = – 2 và a = 1 > 0
   Ta có bảng xét dấu
   

   Từ bảng xét dấu ta có x² + 4x + 4 > 0 với mọi x \( \in \) (– ∞; – 2)\( \cup \)(– 2; + ∞).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tập nghiệm của bất phương trình x2 – 1 > 0 là:
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình x² – 1 > 0 là:

   A. (1; + ∞);

   B. (– 1; + ∞);

   C. (– 1; 1);

   D. (– ∞; – 1)\( \cup \)(1; + ∞) ;

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Tam thức bậc hai f(x) = x² – 1 có ∆ = 4 > 0; hai nghiệm phân biệt là x = – 1; x = 1 và a = 1 > 0
   Ta có bảng xét dấu
   

   Từ bảng xét dấu ta có x² – 1 > 0 với mọi x \( \in \) (–∞; –1)\( \cup \)(1; +∞).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tập nghiệm của bất phương trình x2 – x – 6 ≤ 0 là:
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình x² – x – 6 ≤ 0 là:

   A. (–∞; – 3]\( \cup \)[2; + ∞);

   B. [– 3; 2];

   C. [– 2; 3];

   Đáp án chính xác

   D. (– ∞; – 2]\( \cup \)[3; + ∞) ;

   Trả lời:

   Đáp án đúng là: C
   Tam thức bậc hai f(x) = x² – x – 6 có ∆ = 25 > 0; hai nghiệm phân biệt là x = – 2; x = 3 và a = 1 > 0
   Ta có bảng xét dấu

   x

   –∞              –2                  3                  + ∞

   f(x)

              +        0         –       0         +

   Từ bảng xét dấu ta có x² – x – 6 ≤ 0 với mọi x \( \in \) [– 2; 3].

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tập ngiệm của bất phương trình x(x + 5) ≤ 2(x2 + 2) là
   
   

   Câu hỏi:
   

   Tập ngiệm của bất phương trình x(x + 5) ≤ 2(x² + 2) là

   A. (– ∞; 1]\( \cup \)[4; + ∞)

   Đáp án chính xác

   B. [1; 4];

   C. (– ∞; 1)\( \cup \)(4; + ∞);

   D. (1; 4).

   Trả lời:

   Đáp án đúng là: A
   Ta có: x(x + 5) ≤ 2(x² + 2) \( \Leftrightarrow \) x² – 5x + 4 ≥ 0.
   Xét tam thức f(x) = x² – 5x + 4 có ∆ = 9 > 0, hai nghiệm phân biệt là x = 1; x = 4 và a = 1 > 0.
   Ta có bảng xét dấu :

   x

   – ∞                1                 4                  + ∞

   f(x)

              +        0        –       0         +

   Từ bảng xét dấu ta có  tập nghiệm của bất phương trình là (– ∞; 1]\( \cup \)[4; + ∞).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm tất cả các giá trị của m để bất phương trình mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị của m để bất phương trình mx² – x + m ≥ 0 với mọi x \( \in \) ℝ

   A. m = 0;

   B. m < 0;

   C. 0 < m ≤ \(\frac{1}{2}\);

   D. m ≥ \(\frac{1}{2}\);

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Đặt f(x) = mx² – x + m là tam thức bậc hai với a = m, b = – 1 và c = m
   Với m = 0 thì f(x) = – x , f(x) ≥ 0 ⇔ – x ≥ 0 ⇔ x ≤ 0. Vậy m = 0 không thỏa mãn.
   Với m ≠ 0 thì f(x) = mx² – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta = {1^2} – 4.m.m \le 0\end{array} \right.\)
   \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\1 – 4{m^2} \le 0\end{array} \right.\)
   Xét f(m) = 1 – 4m² có ∆ = 16 > 0, hai nghiệm phân biệt là x = \( – \frac{1}{2}\); x = \(\frac{1}{2}\) và a = – 4 < 0. Ta có bảng xét dấu
   

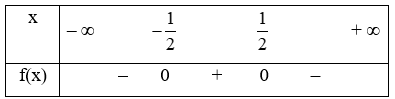
   Từ bảng xét dấu ta có để 1 – 4m² ≤ 0 thì m\( \in \left( { – \infty ; – \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\)
   Vậy để mx² – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m \le  – \frac{1}{2}\\m \ge \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \ge \frac{1}{2}\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====