Câu hỏi:
Tính giá trị \(M = A_{n – 15}^2 + 3A_{n – 14}^3\), biết rằng \(C_n^4 = 20C_n^2\)
A. M = 78;
Đáp án chính xác
B. M = 18;
C. M = 96;
D. M = 84.
Trả lời:
Đáp án đúng là: A
Điều kiện n ≥ 17; n \( \in \) ℕ, ta có \(C_n^4 = 20C_n^2\)\( \Leftrightarrow \frac{{n!}}{{4!\left( {n – 4} \right)!}} = 20\frac{{n!}}{{2!\left( {n – 2} \right)!}}\)
\( \Leftrightarrow \) (n – 2)(n – 3) = 240\( \Rightarrow \left[ \begin{array}{l}n = 18\\n = – 13\end{array} \right.\)
Kết hợp với điều kiện n = 18 thoả mãn. Vậy \(M = A_3^2 + 3A_4^3\) = 78.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm số hạng chứa x4 trong khai triển \({\left( {{x^2} – \frac{1}{x}} \right)^n}\) biết \(A_n^2 – C_n^2 = 10\)
Câu hỏi:
Tìm số hạng chứa x4 trong khai triển \({\left( {{x^2} – \frac{1}{x}} \right)^n}\) biết \(A_n^2 – C_n^2 = 10\)
A. – 20;
B. 10;
Đáp án chính xác
C. – 10;
D. 20.
Trả lời:
Đáp án đúng là: B
Ta có: \(A_n^2 – C_n^2 = 10\)\( \Leftrightarrow \frac{{n!}}{{\left( {n – 2} \right)!}} – \frac{{n!}}{{2!\left( {n – 2} \right)!}} = 10\)
\( \Leftrightarrow \frac{{n(n – 1)(n – 2)…1}}{{(n – 2)…1}} – \frac{{n(n – 1)(n – 2)…1}}{{2.(n – 2)…1}} = 10\)
\( \Leftrightarrow \) n(n – 1) – \(\frac{1}{2}\) n(n – 1) = 10
\( \Leftrightarrow \) \(\frac{1}{2}\)n(n – 1) = 10 \( \Leftrightarrow \) n2 – n – 20 = 0\( \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = – 4\,\end{array} \right.\).
Kết hợp với điều kiện n = 5 thoả mãn
Nhị thức \({\left( {{x^2} – \frac{1}{x}} \right)^n}\)
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = x2, b = \( – \frac{1}{x}\) vào trong công thức ta có
\(C_5^k\)(x2)5 – k .\({\left( { – \frac{1}{x}} \right)^k}\) = ( –1)k\(C_5^k\)(x)10 – 3k
Số hạng cần tìm chứa x4 nên ta có 10 – 3k = 4
Vậy k = 2 thoả mãn bài toán
Vậy hệ số của số hạng không chứa x trong khai triển là: ( –1)2\(C_5^2\) = 10====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
Câu hỏi:
Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
A. 6;
B. 12;
Đáp án chính xác
C. 18;
D. 36.
Trả lời:
Đáp án đúng là: B
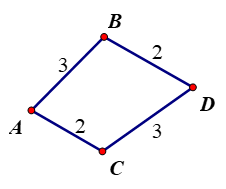
Đi từ thành phố A đến thành phố D ta có các trường hợp sau:
Trường hợp 1. Đi từ thành phố A đến thành phố B rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố B có 3 cách, đi là từ thành phố B đến thành phố D có 2 cách
Vậy trường hợp 1 có 3.2 = 6 cách
Trường hợp 2. Đi từ thành phố A đến thành phố C rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố C có 2 cách ,đi là từ thành phố C đến thành phố D có 3 cách
Vậy trường hợp 2 có 2.3 = 6 cách
Để đi từ thành phố A đến thành phố D ta có 6 + 6 = 12 cách.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3.
Câu hỏi:
Cho các số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3.
A. 5120;
B. 3523;
C. 2520;
Đáp án chính xác
D. 3145.
Trả lời:
Đáp án đúng là: C
Gọi số cần lập \(\overline {abc} \), a ≠ 0.
Trường hợp 1: c = 1
Số a, b được lập từ các cặp số sau: {2; 3}; {3; 5}. Mỗi cặp lập được 2 số nên có 2.2 = 4 số
Trường hợp 2: c = 3
Số a, b được lập từ các cặp số sau: {1; 2}; {1; 5}; {2; 4}; {4; 5}. Mỗi cặp số lập được 2 số nên có 4.2 = 8 số
Trường hợp 3: c = 5
Số a, b được lập từ các cặp số sau: {1; 3}; {3; 4}. Mỗi cặp số lập được 2 số nên có 2.2 = 4 số
Số các số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3 là: 3 + 8 + 4 = 15 (số)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
Câu hỏi:
Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
A. 392;
Đáp án chính xác
B. 1023;
C. 3014;
D. 391.
Trả lời:
Đáp án đúng là: A
Ta chọn các quả cầu theo trình tự sau:
Công đoạn 1, Chọn quả cầu xanh: 7 cách chọn (Vì cầu xanh được chọn tuỳ ý từ 1 đến 7)
Công đoạn 2, Chọn quả cầu vàng: có 7 cách chọn (Vì số đánh trên cầu vàng không được chọn lại số đã đánh trên quả cầu xanh đã chọn)
Công đoạn 3, Chọn quả cầu đỏ: có 8 cách chọn (Vì số trên quả cầu đỏ chọn không được chọn lại các số mà quả cầu xanh và quả cầu vàng đã chọn)
Tổng kết, số cách lấy ra 3 quả cầu khác màu và khác số là 7.7.8 = 392 cách chọn====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lớp 10A có 15 học sinh nam và 25 học sinh nữ. Thầy giáo có bao nhiêu cách chọn ra một học sinh nam và một học sinh nữ để thi đấu cầu lông đôi nam nữ.
Câu hỏi:
Lớp 10A có 15 học sinh nam và 25 học sinh nữ. Thầy giáo có bao nhiêu cách chọn ra một học sinh nam và một học sinh nữ để thi đấu cầu lông đôi nam nữ.
A. 15;
B. 25;
C. 40;
D. 375.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
chọn học sinh nam có 15 cách
chọn học sinh nữ có 25 cách
Tổng kết, áp dụng quy tắc nhân có 15.25 = 375 (cách chọn)====== **** mời các bạn xem câu tiếp bên dưới **** =====