50 Bài tập về phương trình (có đáp án)- Toán 8

Bài tập Toán 8 Chương 3 Bài 1: Mở đầu về phương trình 

A. Bài tập Mở đầu về phương trình

I. Bài tập trắc nghiệm

Bài 1: Trong các phương trình sau, phương trình nào là phương trình một ẩn?

A. 2x = x + 1.

B. x + y = 3x.

C. 2a + b = 1.

D. xyz = xy.

Lời giải:

+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.

+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.

Nhận xét:

+ Đáp án A: là phương trình một ẩn là x

+ Đáp án B: là phương trình hai ẩn là x,y

+ Đáp án C: là phương trình hai ẩn là a,b

+ Đáp án D: là phương trình ba ẩn là x,y,z

Chọn đáp án A.

Bài 2: Nghiệm x = – 4 là nghiệm của phương trình ?

A. – 2,5x + 1 = 11.

B. – 2,5x = – 10

C. 3x – 8 = 0

D. 3x – 1 = x + 7

Lời giải:

+ Đáp án A: – 2,5x + 1 = 11 ⇔ – 2,5x = 10 ⇔ x = $\frac{10}{(–2,5)}$ = – 4 → Đáp án A đúng.

+ Đáp án B: – 2,5x = – 10 ⇔ x = $\frac{\left(–10\right)}{\left(–0,25\right)}$ = 4 → Đáp án B sai.

+ Đáp án C: 3x – 8 = 0 ⇔ 3x = 8 ⇔ x = $\frac{8}{3}$ → Đáp án C sai.

+ Đáp án D: 3x – 1 = x + 7 ⇔ 3x – x = 7 + 1 ⇔ 2x = 8 ⇔ x = 4 → Đáp án D sai.

Chọn đáp án A.

Bài 3: Trong các phương trình sau, cặp phương trình nào tương đương?

A. x = 1 và x( x – 1 ) = 0

B. x – 2 = 0 và 2x – 4 = 0

C. 5x = 0 và 2x – 1 = 0

D. x² – 4 = 0 và 2x – 2 = 0

Lời giải:

Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.

Đáp án A:

+ Phương trình x = 1 có tập nghiệm S = { 1 }

+ Phương trình x( x – 1 ) = 0 ⇔ có tập nghiệm là S = { 0;1 }

→ Hai phương trình không tương đương.

Đáp án B:

+ Phương trình x – 2 = 0 có tập nghiệm S = { 2 }

+ Phương trình 2x – 4 = 0 có tập nghiệm là S = { 2 }

→ Hai phương trình tương đương.

Đáp án C:

+ Phương trình 5x = 0 có tập nghiệm là S = { 0 }

+ Phương trình 2x – 1 = 0 có tập nghiệm là S = { $\frac{1}{2}$ }

→ Hai phương trình không tương đương.

Đáp án D:

+ Phương trình x² – 4 = 0 ⇔ x = ± 2 có tập nghiệm là S = { ± 2 }

+ Phương trình 2x – 2 = 0 có tập nghiệm là S = { 1 }

→ Hai phương trình không tương đương.

Chọn đáp án B.

Bài 4: Tập nghiệm của phương trình 3x – 6 = 0 là ?

A. S = { 1 }

B. S = { 2 }

C. S = { – 2 }

D. S = { 1 }

Lời giải:

Ta có: 3x – 6 = 0 ⇔ 3x = 6 ⇔ x = 2

→ Phương trình có tập nghiệm là S = { 2 }

Chọn đáp án B.

Bài 5: Phương trình $–\frac{1}{2x}$ = – 2 có nghiệm là ?

A. x = – 2.   

B. x = – 4.

C. x = 4.   

D. x = 2.

Lời giải:

Ta có:

Vậy phương trình có tập nghiệm là x = 4.

Chọn đáp án C.

Bài 6: Giải phương trình: (2x + 4).(4 – x) = 0

A. S = {-2; 4}    

B. S = {2; 4}

C. S = {2; – 4}    

D. S = {-2; – 4}

Lời giải:

Ta có: (2x + 4).(4 – x) = 0 khi và chỉ khi:

(2x + 4) = 0 hoặc 4 – x = 0

* 2x + 4 = 0 khi x = -2

* 4 – x = 0 khi x = 4

Vậy tập nghiệm của phương trình là: S = {-2; 4}.

Chọn đáp án A

Bài 7: Hỏi x = 3 là nghiệm của phương trình nào?

A. 2x + 6 = 0    

B. 6 – 2x = 0

C. 3 + x = 0    

D. 3x + 1 = 0

Lời giải:

Xét phương án B: Với x = 3 thì

VT = 6 – 2x = 6 – 2.3 = 0 = VP

Do đó, x = 3 là nghiệm của phương trình 6 – 2x = 0

Chọn đáp án B

Bài 8: Phương trình 2x + 4 = x – 3 + 2x tương đương với phương trình nào sau đây ?

A. –x = 7    

B. 2x + 4 = 0

C. –x = – 7    

D. 2x – 4 = 0

Lời giải:

Chọn đáp án A

Bài 9: Phương trình x² + 2x + 2 = (x – 2)² có mấy nghiệm

A. 0    

B. 1

C. 2    

D. 3

Lời giải:

Chọn đáp án B

Bài 10: Tìm tập nghiệm của phương trình:

A. S = {11}     

B. S = {-11}

C. S = ∅    

D. S = {0}

Lời giải:

Chọn đáp án

II. Bài tập tự luận có lời giải

Bài 1: Có bao nhiêu nghiệm của phương trình |x + 3| = 7?

A. 2                

B. 1                

C. 0                

D. 4

Lời giải

Ta có: 

Vậy phương trình có hai nghiệm x = 4; x = -10

Đáp án cần chọn là: A

Bài 2 Số nghiệm của phương trình 5 – |2x + 3| = 0 là

A. 2                

B. 1                

C. 0                

D. 4

Lời giải

Vậy phương trình có hai nghiệm x = 1; x = -4

Đáp án cần chọn là: A

Bài 3 Hai phương trình nào sau đây là hai phương trình tương đương?

A. x – 2 =4 và x + 1 = 2                     

B. x = 5 và x² = 25

C. 2x² – 8 = 0 và |x| = 2                     

D. 4 + x = 5 và x³ – 2x = 0

Hướng dẫn giải

Lời giải

+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương

+) Xét phương trình x² = 25 ⇔ x = ±5 nên phương trình x² = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x² = 25 không tương đương.

+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x³ – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x³ – 2x = 0 không tương đương.

+) Xét phương trình 2x² – 8 = 0 ⇔ 2x² = 8 ⇔ x² = 4 ⇔  

Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.

Bài 4 Số cặp phương trình tương đương trong các cặp phương trình sau là:

(I) x – 2 =4 và x + 1 = 2                                 

(II) x = 5 và x² = 25

(III) 2x² – 8 = 0 và |x| = 2                              

(IV) 4 + x = 5 và x³ – 2x = 0

Hướng dẫn giải

Lời giải

+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương

+) Xét phương trình x² = 25 ⇔ x = ±5 nên phương trình x² = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x² = 25 không tương đương.

+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x³ – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x³ – 2x = 0 không tương đương.

+) Xét phương trình 2x² – 8 = 0 ⇔ 2x² = 8 ⇔ x² = 4 ⇔  

Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.

Vậy chỉ có 1 cặp phương trình tương đương trong các cặp đã cho

Bài 5 Phương trình nào nhận x = a (a là hằng số khác 0 và 1) làm nghiệm

Lời giải

Thay x = a vào từng phương trình ta được

+) 5.a – 3a = 2 ⇔ 2a = 2 ⇔ a = 1 (loại) nên x = a không là nghiệm của phương trình 5x – 3a = 2

+) a² = a ⇔  (loại) nên x = a không là nghiệm của phương trình x² = a

+)  (loại) nên x = a không là nghiệm của phương trình 

+) a² – a.a = a² – a² = 0 nên x = a là nghiệm của phương trình x² – a.x = 0

III. Bài tập vận dụng

Bài 1 Hãy cho ví dụ về:

a) Phương trình với ẩn y.

b) Phương trình với ẩn u.

Bài 2 Khi x = 6, tính giá trị mỗi vế của phương trình: 2x + 5 = 3(x – 1) + 2.

Bài 3 Cho phương trình 2(x + 2) – 7 = 3 – x

a) x = – 2 có thỏa mãn phương trình không ?

b) x = 2 có là một nghiệm của phương trình không ?

Bài 4 Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không:

a) 4x – 1 = 3x – 2;

b) x + 1 = 2(x – 3);

c) 2(x + 1) + 3 = 2 – x

Bài 5 Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)² = 3t + 4?

Bài 6 Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.

Bài 7 Nối mỗi phương trình sau với các nghiệm của nó (theo mẫu):

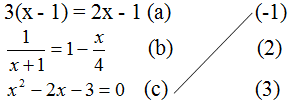
Bài 8 Hai phương trình x = 0 và x(x – 1) = 0 có tương đương không? Vì sao?

B. Lý thuyết Mở đầu về phương trình

1. Khái niệm phương trình một ẩn

– Phương trình một ẩn $x$ là phương trình có dạng:

                             A(x) = B(x)

trong đó A(x) và B(x) là các biểu thức của biến x.

– Ví dụ:

+ Phương trình $3x^2-2=5x+\frac{1}{x}$ là phương trình ẩn x.

+ Phương trình $3\left(t^2-t\right)=\sqrt{t}-\frac{5}{t}$ là phương trình ẩn t.

2. Các khái niệm khác liên quan

– Giá trị $x_0$ được gọi là nghiệm của phương trình A(x) = B(x) nếu đẳng thức $A\left(x_0\right)=B\left(x_0\right)$  đúng.

– Giải phương trình là đi tìm tất cả các nghiệm của phương trình đó.

– Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

Chú ý: Hai phương trình cùng vô nghiệm tương đương nhau.