Lý thuyết Toán 10 Chương 6 (Chân trời sáng tạo 2023): Thống kê hay, chi tiết

Lý thuyết Toán lớp 10 Chương 6: Thống kê

A. Lý thuyết Chương 6: Thống kê

1. Số gần đúng

Trong thực tế cuộc sống cũng như trong khoa học kĩ thuật, có nhiều đại lượng mà ta không thể xác định được giá trị chính xác. Mỗi dụng cụ hay phương pháp đo khác nhau có thể sẽ cho ra các kết quả khác nhau. Vì vậy kết quả thu được thường chỉ là những số gần đúng.

2. Sai số tuyệt đối và sai số tương đối

2.1. Sai số tuyệt đối

Nếu a là số gần đúng của số đúng $\overline{a}$ thì ${\Delta }_a=\left|\overline{a}-a\right|$  được gọi là sai số tuyệt đối của số gần đúng a.

* Độ chính xác:

Trên thực tế ta thường không biết số đúng $\overline{a}$ nên không thể tính được chính xác ∆_a. Khi đó, ta thường tìm cách khống chế sai số tuyệt đối ∆_a không vượt quá mức d > 0 cho trước:

${\Delta }_a=\left|\overline{a}-a\right|\le d$ hay a – d ≤ $\overline{a}$  ≤ a + d.

Khi đó, ta nói a là số gần đúng của số đúng $\overline{a}$  với độ chính xác d.

Quy ước viết gọn: $\overline{a}=a\pm d$ .

2.2. Sai số tương đối

Sai số tương đối của số gần đúng a, kí hiệu là δ_a, là tỉ số giữa sai số tuyệt đối ∆_a và |a|, tức là ${\delta }_a=\frac{{\Delta }_a}{\left|a\right|}$ .

Nếu  thì ∆_a ≤ d. Do đó ${\delta }_a=\frac{{\Delta }_a}{\left|a\right|}$. Nếu δ_a hay $\frac{d}{\left|a\right|}$ càng nhỏ thì chất lượng của phép đo đạc hay tính toán càng cao.

Chú ý: Người ta thường viết sai số tương đối dưới dạng phần trăm.

3. Số quy tròn

3.1. Quy tắc làm tròn số

Quy tắc làm tròn số đến một hàng nào đó (gọi là hàng quy tròn):

+ Nếu chữ số sau hàng quy tròn nhỏ hơn 5 thì ta thay nó và các chữ số bên phải nó bởi chữ số 0.

+ Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên nhưng cộng thêm 1 đơn vị vào chữ số hàng quy tròn.

Chú ý:

+ Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Ta có thể nói độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn.

+ Khi quy tròn số đúng $\overline{a}$ đến một hàng nào đó thì ta nói số gần đúng a nhận được là chính xác đến hàng đó. Ví dụ số gần đúng của π chính xác đến hàng phần trăm là 3,14.

3.2. Xác định số quy tròn của số gần đúng với độ chính xác cho trước

Các bước xác định số quy tròn của số gần đúng a với độ chính xác d cho trước:

Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.

Bước 2: Quy tròn số a ở hàng gấp 10 lần hàng tìm được ở Bước 1.

3.3. Xác định số gần đúng của một số với độ chính xác cho trước

Để tìm số gần đúng a của số đúng $\overline{a}$ với độ chính xác d, ta thực hiện các bước sau:

Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.

Bước 2: Quy tròn $\overline{a}$ đến hàng tìm được ở trên.

4. Bảng số liệu

Dựa vào các thông tin đã biết và sử dụng mối liên hệ toán học giữa các số liệu, ta có thể phát hiện ra được số liệu không chính xác trong một số trường hợp.

5. Biểu đồ

Ta có thể biểu diễn số liệu thống kê dưới dạng biểu đồ.

Một số dạng biểu đồ thường gặp: biểu đồ cột, biểu đồ cột kép, biểu đồ quạt, biểu đồ tranh,…

Quan sát các biểu đồ ta có thể đưa ra các nhận xét về số liệu thống kê.

6. Số trung bình

6.1. Công thức tính số trung bình

• Giả sử ta có một mẫu số liệu là x₁, x­₂, …, x_n.

Số trung bình (hay số trung bình cộng) của mẫu số liệu này, kí hiệu là $\overline{x}$ , được tính bởi công thức

$\overline{x}=\frac{x_1+x_2+\mathrm{\dots }+x_n}{n}$.

• Giả sử mẫu số liệu được cho dưới dạng bảng tần số

Giá trị	x1	x2	…	xk
Tần số	n1	n2	…	nk

Khi đó, công thức tính số trung bình trở thành

$\overline{x}=\frac{n_1{x}_1+n_2{x}_2+\mathrm{\dots }+n_k{x}_k}{n}$.

Trong đó n = n₁ + n₂ + … + n_k. Ta gọi n là cỡ mẫu.

Chú ý: Nếu kí hiệu $f_k=\frac{n_k}{n}$ là tần số tương đối (hay còn gọi là tần suất) của x_k­ trong mẫu số liệu thì số trung bình còn có thể biểu diễn là: $\overline{x}=f_1{x}_1+f_2{x}_2+\mathrm{\dots }+f_k{x}_k$.

6.2.Ý nghĩa của số trung bình

Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.

7. Trung vị và tứ phân vị

7.1. Trung vị

7.1.1 Định nghĩa và cách tính số trung vị

Khi các số liệu trong mẫu số liệu chênh lệch nhau quá lớn, ta dùng một đặc trưng khác của mẫu số liệu, gọi là trung vị để so sánh các mẫu số liệu với nhau.

Trung vị được định nghĩa như sau:

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

Trung vị của mẫu, kí hiệu là M_e, là giá trị ở chính giữa dãy x₁, x­­₂, …, x_n. Cụ thể:

– Nếu n = 2k + 1, (tức n là số tự nhiên lẻ), thì trung vị của mẫu M_e = x_{k + 1}.

– Nếu n = 2k,  (tức n là số tự nhiên chẵn), thì trung vị của mẫu M_e = $\frac{1}{2}\left(x_k+x_{k+1}\right)$ .

7.1.2 Ý nghĩa của số trung vị

Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu. Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị. Khi trong mẫu xuất hiện thêm một giá trị rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì ít thay đổi.

7.2. Tứ phân vị

• Trung vị chia mẫu thành hai phần. Trong thực tế người ta cũng quan tâm đến trung vị của mỗi phần đó. Ba trung vị này được gọi là tứ phân vị của mẫu.

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

Tứ phân vị của một mẫu số liệu gồm ba giá trị, gọi là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là Q₁, Q₂, Q­₃). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:

– Giá trị tứ phân vị thứ hai, Q₂, chính là số trung vị của mẫu.

– Giá trị tứ phân vị thứ nhất, Q₁, là trung vị của nửa số liệu đã sắp xếp bên trái Q₂ (không bao gồm Q₂ nếu n lẻ).

– Giá trị tứ phân vị thứ ba, Q₃, là trung vị của nửa số liệu đã sắp xếp bên phải Q₂ (không bao gồm Q₂ nếu n lẻ).

• Ý nghĩa của tứ phân vị

Các điểm tứ phân vị Q₁, Q₂, Q₃ chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần chia khoảng 25% tổng số liệu đã thu thập được.

Tứ phân vị thứ nhất Q₁ còn được gọi là tứ phân vị dưới và đại diện cho nửa mẫu số liệu phía dưới. Tứ phân vị thứ ba Q₃, còn được gọi là tứ phân vị trên và đại diện cho nửa mẫu số liệu ở phía trên.

8. Mốt

Cho mẫu số liệu dưới dạng bảng tần số. Giá trị có tần số lớn nhất được gọi là mốt của mẫu số liệu và kí hiệu là M_o.

Ý nghĩa của mốt: Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.

Chú ý: Một mẫu số liệu có thể có rất nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.

9. Khoảng biến thiên và khoảng tứ phân vị

9.1. Khoảng biến thiên và khoảng tứ phân vị

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

• Khoảng biến thiên của một mẫu số liệu, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là:

R = x_n – x₁.

• Khoảng tứ phân vị, kí hiệu là ∆_Q, là hiệu giữa Q_3­ và Q₁, tức là:

∆_Q = Q₃ – Q₁.

9.2. Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị

Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.

Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ Q₁ đến Q₃ trong mẫu.

Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.

9.3. Giá trị ngoại lệ 

Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu, đó là các giá trị quá nhỏ hay quá lớn so với đa số các giá trị của mẫu. Cụ thể, phần tử x trong mẫu là giá trị ngoại lệ nếu x > Q₃ + 1,5∆_Q hoặc x < Q₁ – 1,5∆_Q.

Sự xuất hiện của các giá trị ngoại lệ làm cho số trung bình và phạm vi của mẫu thay đổi lớn. Do đó, khi mẫu có giá trị ngoại lệ, người ta thường sử dụng trung vị và khoảng tứ phân vị để đo mức độ tập trung và mức độ phân tán của đa số các phần tử trong mẫu số liệu.

10. Phương sai và độ lệch chuẩn

10.1. Công thức tính phương sai và độ lệch chuẩn

* Giả sử ta có một mẫu số liệu là x₁, x₂, …, x_n.

• Phương sai của mẫu số liệu này, kí hiệu là S², được tính bởi công thức:$S^2=\frac{1}{n}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{\dots }+{\left(x_n-\overline{x}\right)}^2\right],$

 

trong đó $\overline{x}$ là số trung bình của mẫu số liệu.

• Căn bậc hai của phương sai được gọi là độ lệch chuẩn, kí hiệu là S.

Chú ý: Có thể biến đổi công thức tính phương sai ở trên thành:

$S^2=\frac{1}{n}\left(x_1^2+x_2^2+\mathrm{\dots }+x_n^2\right)-{\overline{x}}^2$.

Trong thống kê, người ta cũng quan tâm đến phương sai hiệu chỉnh, kí hiệu là , được tính bởi công thức:

${\widehat{s}}^2=\frac{1}{n-1}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{\dots }+{\left(x_n-\overline{x}\right)}^2\right]$.

* Giả sử mẫu số liệu được cho dưới dạng bảng tần số:

Giá trị	x1	x2	…	xk
Tần số	n1	n2	…	nk

Khi đó, công thức tính phương sai trở thành:

$S^2=\frac{1}{n}\left[n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{\dots }+n_k{\left(x_k-\overline{x}\right)}^2\right],$

trong đó n = n₁ + n₂ + … + n_k.

Có thể biến đổi công thức tính phương sai trên thành

$S^2=\frac{1}{n}\left(n_1{x}_1^2+n_2{x}_2^2+\mathrm{\dots }+n_k{x}_k^2\right)-\overline{x}$.

10.2. Ý nghĩa của phương sai và độ lệch chuẩn

Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.

Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình. Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau (có độ phân tán lớn).

B. Bài tập tự luyện

Bài 1. Cho số $\sqrt{5}=2,\mathrm{236067977\dots }$.

a) Hãy quy tròn $\sqrt{5}$ đến hàng phần trăm.

b) Hãy tìm số gần đúng của $\sqrt{5}$ với độ chính xác 0,005.

Hướng dẫn giải

a) Quy tròn số $\sqrt{5}$ đến hàng phần trăm ta được số gần đúng là 2,24.

Vậy $\sqrt{5}\approx 2,24$ (quy tròn đến hàng phần trăm).

b) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác 0,005 là hàng phần nghìn. Quy tròn $\sqrt{5}$ đến hàng phần nghìn ta được số gần đúng là 2,236.

Vậy $\sqrt{5}\approx 2,24$ với độ chính xác 0,005.

Bài 2. Làm tròn số 4372,8 đến hàng chục và 8,125 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

Hướng dẫn giải

+ Số quy tròn của số 4372,8 đến hàng chục là 4370. Sai số tuyệt đối là

∆ = |4370 − 4372,8| = 2,8.

+ Số quy tròn của số 8,125 đến hàng phần trăm là 8,13. Sai số tuyệt đối là

∆’ = |8,13 – 8,125| = 0,005.

Bài 3. Hãy viết số quy tròn của số gần đúng trong những trường hợp sau:

a) 3678008 ± 1000;

b) 21,02345 ± 0,001.

Hướng dẫn giải

a) 3678008 ± 1000

Hàng lớn nhất của độ chính xác d = 1000 là hàng nghìn, nên ta quy tròn đến hàng phần chục nghìn.

Vậy số quy tròn trong trường hợp này là 3680000.

b) 21,02345 ± 0,001

Hàng lớn nhất của độ chính xác d = 0,001 là hàng phần nghìn, nên ta quy tròn đến hàng phần trăm.

Vậy số quy tròn cần tìm là 21,02.

Bài 4. Một tam giác có ba cạnh đo được như sau: a = 5,4 cm ± 0,2 cm; b = 7,2 cm ± 0,2 cm và c = 9,7 cm ± 0,1 cm. Tính chu vi của tam giác đó.

Hướng dẫn giải

Chu vi của tam giác là:

P = a + b + c = (5,4 ± 0,2) + (7,2 ± 0,2) + (9,7 ± 0,1)

= (5,4 + 7,2 + 9,7) ± (0,2 + 0,2 + 0,1)

= 22,3 ± 0,5  (cm).

Vậy chu vi của tam giác đã cho là P = 22,3 cm ± 0,5 cm.

Bài 5. Một đội gồm 15 thợ điêu khắc được chia đều vào 3 tổ. Trong một ngày, mỗi người thợ làm được 2 hoặc 3 sản phẩm. Cuối ngày, đội trưởng thống kê lại số sản phẩm mà mỗi tổ làm được ở bảng sau:

Tổ	1	2	3
Số sản phẩm	10	15	17

Đội trưởng đã thống kê đúng chưa? Tại sao?

Hướng dẫn giải

Mỗi tổ có 15 : 3 = 5 người thợ.

Trong một ngày, mỗi người thợ làm được 2 hoặc 3 sản phẩm nên mỗi tổ làm được từ 10 đến 15 sản phẩm. Do đó, bảng trên ghi Tổ 4 làm được 17 sản phẩm là không chính xác.

Vậy đội trưởng thống kê chưa đúng.

Bài 6. Sản lượng nuôi tôm phân theo địa phương của các tỉnh Cà Mau và Tiền Giang được thể hiện ở hai biểu đồ sau (đơn vị: tấn):

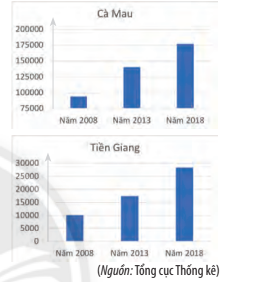
a) Hãy cho biết các phát biểu sau là đúng hay sai:

i. Sản lượng nuôi tôm mỗi năm của tỉnh Tiền Giang đều cao hơn tỉnh Cà Mau.

ii. Ở tỉnh Cà Mau, sản lượng nuôi tôm năm 2018 tăng gấp hơn 4 lần so với năm 2008.

iii. Ở tỉnh Tiền Giang, sản lượng nuôi tôm năm 2018 tăng gấp hơn 2,5 lần so với năm 2008.

b) Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ nào?

Hướng dẫn giải

a)

i. Quan sát biểu đồ ta thấy:

Sản lượng nuôi tôm mỗi năm ở Tiền Giang đều thấp hơn 30 000 tấn, sản lượng nuôi tôm mỗi năm ở Cà Mau đều cao hơn 75 000 tấn. 

Do đó sản lượng nuôi tôm mỗi năm của tỉnh Cà Mau đều cao hơn rất nhiều so với tỉnh Tiền Giang.

Vậy phát biểu i. là sai.

ii. Ở tỉnh Cà Mau:

– Sản lượng nuôi tôm năm 2018 là 175 000 tấn.

– Sản lượng nuôi tôm năm 2008 khoảng hơn 90 000 tấn.

Vì $\frac{175000}{90000}\approx 2$ .

Do đó sản lượng nuôi tôm năm 2018 ở tỉnh Cà Mau tăng khoảng gần 2 lần so với năm 2008.

Vậy phát biểu ii. là sai.

iii. Ở tỉnh Tiền Giang:

– Sản lượng nuôi tôm năm 2018 khoảng 29 000 tấn.

– Sản lượng nuôi tôm năm 2008 là 10 000 tấn.

Vì $\frac{29000}{10000}=2,9$ .

Do đó sản lượng nuôi tôm năm 2018 ở tỉnh Tiền Giang tăng gấp khoảng 2,9 (> 2,5) lần so với năm 2008.

Vậy phát biểu iii. là đúng.

b) Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ cột ghép.

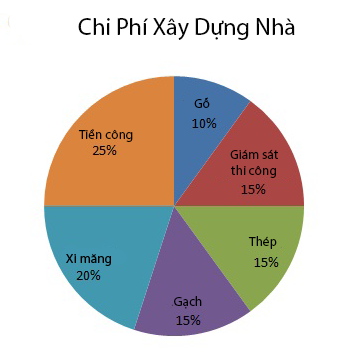
Bài 7. Hoa vẽ biểu đồ biểu thị tỉ lệ chi phí xây dựng nhà ở của gia đình theo bảng thống kê dưới đây:

Loại chi phí	Số tiền (triệu đồng)
Tiền công	250
Gỗ	100
Giám sát thi công	150
Thép	150
Gạch	200
Xi măng	150

Bạn hãy cho biết biểu đồ Hoa vẽ đã chính xác chưa. Nếu chưa thì cần điều chỉnh lại như thế nào cho đúng?

Hướng dẫn giải

Theo bảng thống kê thì các loại chi phí giám sát thi công, thép và xi măng bằng nhau nên trên biểu đồ quạt, hình quạt biểu diễn tỉ lệ giám sát thi công, thép và xi măng phải bằng nhau. Do đó biểu đồ bạn Hoa vẽ chưa chính xác.

Ta cần đổi chỗ phần chữ chú thích trên biểu đồ của xi măng cho gạch thì biểu đồ chính xác.

Bài 8. Hãy tìm số trung bình, tứ phân vị và mốt của mẫu số liệu sau:

56; 45; 65; 45; 56; 78; 100; 78; 78.

Hướng dẫn giải

Cỡ mẫu: n = 9.

Số trung bình: $\overline{x}=\frac{1}{9}\left(56+45+65+45+56+78+100+78+78\right)\approx 66,78$ .

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

45; 45; 56; 56; 65; 78; 78; 78; 100.

Vì cỡ mẫu là 9, là số lẻ nên tứ phân vị thứ hai là Q₂ = 65.

Tứ phân vị thứ nhất là trung vị của mẫu: 45; 45; 56; 56. Do đó Q₁ = $\frac{1}{2}\left(45+56\right)$ = 50,5.

Tứ phân vị thứ ba là trung vị của mẫu: 78; 78; 78; 100. Do đó Q₃ = $\frac{1}{2}\left(78+78\right)$ = 78.

Giá trị 78 có tần số lớn nhất nên mốt của mẫu số liệu là M_o = 78.

Bài 9. Hãy tìm số trung bình, trung vị và mốt của mẫu số liệu sau:

Giá trị	20	25	30	35
Tần số	2	3	5	7

Hướng dẫn giải

Cỡ mẫu n = 2 + 3 + 5 + 7 = 17.

Số trung bình: $\overline{x}=\frac{1}{17}\left(2.20+3.25+5.30+7.35\right)=30$ .

Sắp xếp các số liệu đã cho theo thứ tự không giảm, ta được:

20; 20; 25; 25; 25; 30; 30; 30; 30; 30; 35; 35; 35; 35; 35; 35; 35.

Vì cỡ mẫu là 17 là số lẻ nên trung vị là M_e = 30.

Giá trị 35 có tần số lớn nhất nên mốt của mẫu số liệu là M_o = 35.

Bài 10. Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của một số thí sinh ở bảng sau: 

Thời gian (đơn vị: phút)	5	6	7	8	35
Số thí sinh	1	3	5	2	1

a) Hãy tìm số trung bình, tứ phân vị và mốt của thời gian thi nghề của các thí sinh trên.

b) Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng 7. Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.

Hướng dẫn giải

a) Cỡ mẫu là n = 1 + 3 + 5 + 2 + 1 = 12.

Số trung bình là: $\overline{x}=\frac{1.5+3.6+5.7+2.8+1.35}{12}\approx 9,08$ .

Số thí sinh là trong thời gian 7 phút là nhiều nhất nên mốt của mẫu là M_o = 7.

Sắp xếp các giá trị của mẫu theo thứ tự không giảm, ta được:

5; 6; 6; 6; 7; 7; 7; 7; 7; 8; 8; 35.

Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là Q₂ = $\frac{1}{2}\left(7+7\right)=7$ .

Tứ phân vị thứ nhất là trung vị của mẫu: 5; 6; 6; 6; 7; 7. Do đó Q₁ = 6.

Tứ phân vị thứ ba là trung vị của mẫu: 7; 7; 7; 8; 8; 35. Do đó Q₃ = 7,5.

b) Dựa theo số trung bình, vì 9,08 > 7 nên thời gian thi của các thí sinh năm nay nhiều hơn năm ngoái.

Dựa theo trung vị, thì cả hai năm trung vị đều bằng nhau và bằng 7 nên thời gian của các thí sinh trong hai năm là ngang nhau.

Vì trong mẫu số liệu của năm nay có số liệu 35 lớn hơn so với các số liệu còn lại rất nhiều, do đó ta dùng trung vị để so sánh sẽ phù hợp hơn.

Vậy thời gian thi nói chung của các thí sinh trong hai năm là ngang nhau. 

Bài 11. Người ta đã tiến hành thăm dò ý kiến của khách hàng về các mẫu 1, 2, 3, 4 của một loại sản phẩm mới được sản xuất ở nhà máy. Dưới đây là bảng phân bố tần số theo số phiếu bình chọn tín nhiệm cho các mẫu kể trên.

Mẫu	1	2	3	4	Cộng
Tần số	195	300	356	149	1000

 a) Tìm mốt của mẫu số liệu.

b) Trong sản xuất, nhà máy nên ưu tiên cho mẫu nào?

Hướng dẫn giải

a) Quan sát bảng tần số ta thấy mẫu 3 có tần số lớn nhất nên mốt của mẫu số liệu đã cho là M_o = 3.

b) Vì M_o = 3 nên trong sản xuất, nhà máy nên ưu tiên cho mẫu 3.

Bài 12. Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và các giá trị ngoại lệ (nếu có) của mẫu số liệu sau: 6; 8; 3; 4; 5; 6; 7; 2; 4. 

Hướng dẫn giải

Số trung bình: $\overline{x}=\frac{6+8+3+4+5+6+7+2+4}{9}=5$ .

Phương sai mẫu số liệu là:

$S^2=\frac{1}{9}$(6² + 8² + 3² + 4² + 5² + 6² + 7² + 2² + 4²) – 5² = $\frac{10}{3}$ .

Độ lệch chuẩn mẫu số liệu là: $S=\sqrt{S^2}=\sqrt{\frac{10}{3}}=\frac{\sqrt{30}}{3}$ .

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

2; 3; 4; 4; 5; 6; 6; 7; 8.

Khoảng biến thiên của mẫu là: R = 8 – 2 = 6.

Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q₂ = 5.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 3; 4; 4. Do đó Q₁ = 3,5.

Tứ phân vị thứ ba là trung vị của mẫu: 6; 6; 7; 8. Do đó Q₃ = 6,5.

Khoảng tứ phân vị của mẫu là: ∆_Q = 6,5 – 3,5 = 3.

Ta có: Q₃ + 1,5∆_Q = 6,5 + 1,5 . 3 = 11 và Q₁ – 1,5∆_Q = 3,5 – 1,5 . 3 = – 1.

Do đó mẫu số liệu không có giá trị ngoại lệ.

Bài 13. Hai lớp 10A, 10B của một trường Trung học phổ thông đồng thời làm bài thi môn Toán theo cùng một đề thi. Kết quả thi được trình bày ở hai bảng phân bố tần số sau đây:

Điểm thi Toán của lớp 10A

Điểm thi	5	6	7	8	9	10	Cộng
Tần số	3	7	12	14	3	1	40

 Điểm thi Toán của lớp 10B

Điểm thi	6	7	8	9	Cộng
Tần số	8	18	10	4	40

a) Tính các số trung bình cộng, phương sai, độ lệch chuẩn của các mẫu số liệu đã cho.

b) Xét xem kết quả làm bài thi môn Toán ở lớp nào đồng đều hơn?

Hướng dẫn giải

a)

* Lớp 10A:

Số trung bình: $\overline{x_A}=\frac{1}{40}$ (3 . 5 + 7 . 6 + 12 . 7 + 14 . 8 + 3 . 9 + 1 . 10) = 7,25.

Phương sai mẫu số liệu:

$S_A^2=\frac{1}{40}$(3 . 5² + 7 . 6² + 12 . 7² + 14 . 8² + 3 . 9² + 1 . 10²) – 7,25² = 1,2875.

Độ lệch chuẩn: S_A = $\sqrt{S_A^2}=\sqrt{1,2875}\approx 1,135$ .

* Lớp 10B:

Số trung bình: $\overline{x_B}=\frac{1}{40}$ (8 . 6 + 18 . 7 + 10 . 8 + 4 . 9) = 7,25.

Phương sai mẫu số liệu:

$S_B^2=\frac{1}{40}$(8 . 6² + 18 . 7² + 10 . 8² + 4 . 9²) – 7,25² = 0,7875.

Độ lệch chuẩn: S_B = $\sqrt{S_B^2}=\sqrt{0,7875}\approx 0,887$ .

b) Vì 0,887 < 1,135 nên S_B < S_A hay độ lệch chuẩn của mẫu số liệu lớp 10B nhỏ hơn lớp 10A.

Vậy kết quả làm bài thi của học sinh lớp 10B đồng đều hơn.

Bài 14. Kết quả điều tra mức lương hằng tháng của một số công nhân của hai nhà máy A và B được cho ở bảng sau (đơn vị: triệu đồng):

a) Hãy tìm số trung bình, mốt, tứ phân vị và độ lệch chuẩn của hai mẫu số liệu lấy từ nhà máy A và nhà máy B.

b) Hãy tìm các giá trị ngoại lệ trong mỗi mẫu số liệu trên. Công nhân nhà máy nào có mức lương cao hơn? Tại sao?

Hướng dẫn giải

a)

* Nhà máy A:

+ Số trung bình mức lương hàng tháng: $\overline{x_A}=\frac{4+5+5+47+5+6+4+4}{8}=10$.

+ Giá trị 4 và 5 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy A là 4 và 5.

+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:

4; 4; 4; 5; 5; 5; 6; 47.

Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q_2A = 5.

Tứ phân vị thứ nhất là trung vị của mẫu: 4; 4; 4; 5. Do đó Q_1A = 4.

Tứ phân vị thứ ba là trung vị của mẫu: 5; 5; 6; 47. Do đó Q_3A = 5,5.

+ Phương sai mẫu:

$S_A^2=\frac{1}{8}$(4² + 5² + 5² + 47² + 5² + 6² + 4² + 4²) – 10² = 196.

+ Độ lệch chuẩn: S_A = $\sqrt{S_A^2}=\sqrt{196}=14$ .

* Nhà máy B:

+ Số trung bình mức lương hàng tháng: $\overline{x_B}=\frac{2+9+9+8+10+9+9+11+9}{9}\approx 8,4$ .

+ Giá trị 9 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy B là 9.

+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:

2; 8; 9; 9; 9; 9; 9; 10; 11.

Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q_2B = 9.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 8; 9; 9. Do đó Q_1B = 8,5.

Tứ phân vị thứ ba là trung vị của mẫu: 9; 9; 10; 11. Do đó Q_3B = 9,5.

+ Phương sai mẫu:

$S_B^2=\frac{1}{9}$(2² + 8² + 9² + 9² + 9² + 9² + 9² + 10² + 11²) – 8,4² = 6,55.

+ Độ lệch chuẩn: S_B = $\sqrt{S_B^2}=\sqrt{6,55}\approx 2,6$ .

b)

+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy A là: ∆_QA = 5,5 – 4 = 1,5.

Ta có: Q_3A + 1,5∆_QA = 5,5 + 1,5 . 1,5 = 7,75 và Q_1A – 1,5∆_QA = 4 – 1,5 . 1,5 = 1,75.

Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy A là 47.

+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy B là: ∆_QB = 9,5 – 8,5 = 1.

Ta có: Q_3B + 1,5∆_QB = 9,5 + 1,5 . 1 = 11 và Q_1B – 1,5∆_QB = 8,5 – 1,5 . 1 = 7.

Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy B là 2.

+ Quan sát các số liệu tính được ở câu a), ta thấy

– Số trung bình mức lương hàng tháng của công nhân ở nhà máy A cao hơn nhà máy B.

– Phương sai mẫu và độ lệch chuẩn mẫu số liệu ở nhà máy A cao hơn nhà máy B nên mức lương hằng tháng của công nhân nhà máy A có độ phân tán cao hơn nhà máy B, do đó mức lương của công nhân nhà máy B ổn định hơn nhà máy A.

– Mức lương xuất hiện nhiều nhất trong mẫu A là 4 và 5 triệu đồng, nhà máy B là 9 triệu đồng.

Do đó, ta có thể khẳng định công nhân nhà máy A có mức lương cao hơn (đều và ổn định hơn).

Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Toán 10 Chương 5: Vectơ

Lý thuyết Toán 10 Chương 6: Thống kê

Lý thuyết Toán 10 Chương 7: Bất phương tình bậc hai một ẩn

Lý thuyết Toán 10 Chương 8: Đại số tổ hợp

Lý thuyết Toán 10 Chương 9: Tọa độ của vectơ