Tài liệu Bài tập Khoảng cách từ chân đường cao đến mặt phẳng bên có đáp án gồm các nội dung chính sau:
A. Phương phương giải
– Gồm phương pháp giải Bài tập Khoảng cách từ chân đường cao đến mặt phẳng bên.
B. Bài tập minh họa
– Gồm 13 bài tập có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Khoảng cách từ chân đường cao đến mặt phẳng bên.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

KHOẢNG CÁCH TỪ CHÂN ĐƯỜNG CAO ĐẾN MẶT PHẲNG BÊN.
A. PHƯƠNG PHÁP GIẢI
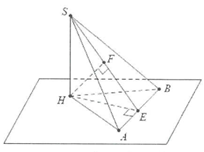
Xét bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ điểm H đến mặt bên .
Dựng ta có:
.
Dựng . Từ
Do đó .
Cách tính: Xét tam giác SHE vuông tại H có đường cao HF ta có:
Hay .
B. BÀI TẬP MINH HỌA
|
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có . Biết và . a) Tính khoảng cách từ A đến mặt phẳng . b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng . |
Lời giải
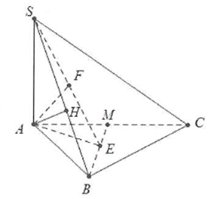
a) Ta có : , mặt khác .
Dựng .
Khi đó .
b) Dựng ta có:
.
Khi đó: .
Ta có: . Do BM là đường trung tuyến ứng với cạnh huyền nên đều cạnh .
Khi đó .
|
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh , . Đường thẳng SB tạo với đáy một góc . a) Tính khoảng cách từ A đến mặt phẳng . b) Tính khoảng cách từ A đến mặt phẳng , với M là trung điểm của cạnh AB. |
Lời giải
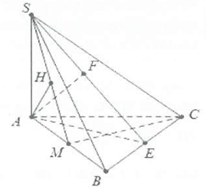
a) Do .
Do đó .
Dựng đều nên .
Dựng , mặt khác .
b) Do M là trung điểm của AB nên .
Mặt khác . Dựng .
Khi đó .
|
Ví dụ 3: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết . Tính khoảng cách d từ O đến mặt phẳng . |
Xem thêm