Bộ 15 Đề thi học kì 2 Toán 12 có đáp án năm 2024

Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 12 bản word có lời giải chi tiết:

B1:   –

B2:   – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi học kì 2 Toán lớp 12 có đáp án năm 2024 (15 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 

Năm học 2023 – 2024

Môn: Toán lớp 12

Thời gian làm bài: 90 phút

(Đề 1)

Câu 1[TH]. Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện \[\left| {z – (3 + 2i)} \right| = 2\] là

  A. Đường tròn tâm I(3;2), bán kính R = 2.   

   B. Đường tròn tâm I(-3;2), bán kính R = 2.

  C. Đường tròn tâm I(3;2), bán kính\[R = \sqrt 2 \].                         

   D. Đường tròn tâm I(3;- 2), bán kính R = 2.

Câu 2[TH]. Cho \[{\rm{w}} = \frac{{z_{}^2 – \left( {\overline z } \right)_{}^2}}{{1 + z.\overline z }}\]với z là số phức tùy ý cho trước. Mệnh đề nào dưới đây đúng?

  A. w là số ảo.             B. w = -1                  

 C. w = 1.                     D. w là số thực.

Câu 3[TH]. Gọi z1, z2, z3, z4 là các nghiệm phức của phương trình

\[(z_{}^2 + z)_{}^2 + 4(z_{}^2 + z) – 12 = 0\]. Tính \[S = \left| {z_1^{}} \right|_{}^2 + \left| {z_2^{}} \right|_{}^2 + \left| {z_3^{}} \right|_{}^2 + \left| {z_4^{}} \right|_{}^2\]

A. \[S = 18\]                 B. \[S = 16\]

C. \[S = 17\]                 D. \[S = 15\]

Câu 4[NB]. Trong không gian với hệ tọa độ Oxyz,

 cho đường thẳng d: \[\left\{ \begin{array}{l}x = 1 – t\\y = 3\\z =  – 1 + 2t\end{array} \right.\], vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?

A. \[\overrightarrow {u_4^{}}  = ( – 1;3;2)\]

B. \[\overrightarrow {u_1^{}}  = (1;0; – 2)\] 

C. \[\overrightarrow {u_2^{}}  = (1;3; – 1)\] 

D. \[\overrightarrow {u_1^{}}  = (1;0;2)\]

Câu 5[NB]. Cho số phức z = 3+ 4i. Mệnh đề nào dưới đây là sai

A. z là số thực.            

B. \[\overline z  = 3 – 4i\]                               

C. Phần ảo của số phức z bằng 4

D. \[\left| z \right| = 5\]

Câu 6[TH]. Trong không gian với hệ tọa độ Oxyz, cho điểm \[A(3; – 2; – 2),B(3;2;0)\]. Phương trình mặt cầu đường kính AB là:

A. \[(x – 3)_{}^2 + y_{}^2 + (z + 1)_{}^2 = 20\]

B. \[(x – 3)_{}^2 + y_{}^2 + (z + 1)_{}^2 = 5\]                               

C. \[(x + 3)_{}^2 + y_{}^2 + (z – 1)_{}^2 = 5\]

D. \[(x + 3)_{}^2 + y_{}^2 + (z – 1)_{}^2 = 20\]                             

Câu 7[VD]. Cửa lớn của một trung tâm giải trí có dạng Parabol (như hình vẽ).

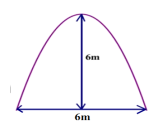
Người ta dự định lắp cửa kính cường lực 12 ly với đơn giá 800.000 đồng/m2.

Tính chi phí để lắp cửa.

A. 9.600.000 đồng

B. 19.200.000 đồng     

C. 33.600.000 đồng

D. 7.200.000 đồng

Câu 8[VD]. Trong không gian với hệ tọa độ Oxyz, cho điểm \[A(2; – 1;1)\] và hai mặt phẳng \[(P):2x – z + 1 = 0,(Q):y – 2 = 0.\]Viết phương trình mặt phẳng \[\left( \alpha  \right)\] đi qua A và vuông góc với hai mặt phẳng (P), (Q).

A. \[(\alpha ):2x – y + z – 4 = 0\]

B. \[(\alpha ):x + 2z – 4 = 0\]

C. \[(\alpha ):2x + y – 4 = 0\]

D. \[(\alpha ):x + 2y + z = 0\]

Câu 9[VD]. Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[A(0;0;1),B( – 1; – 2;0),C(2;0; – 1).\] Tập hợp các điểm M các đều ba điểm A, B, C là đường thẳng \[\Delta \]. Viết phương trình \[\Delta \].

  A. \[\Delta :\left\{ \begin{array}{l}x = \frac{1}{3} + t\\y =  – \frac{2}{3} + t\\z = t\end{array} \right.\]

B. \[\Delta :\left\{ \begin{array}{l}x = \frac{1}{3} + t\\y =  – \frac{2}{3} – t\\z = t\end{array} \right.\]                        

 C. \[\Delta :\left\{ \begin{array}{l}x = 1 + t\\y =  – \frac{3}{2} + t\\z = t\end{array} \right.\]

D. \[\Delta :\left\{ \begin{array}{l}x = \frac{1}{2} + t\\y =  – 1 – t\\z =  – \frac{1}{2} + t\end{array} \right.\]

Câu 10[NB]. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[(P):\frac{x}{2} + \frac{y}{1} + \frac{z}{3} = 1\], vecto nào dưới đây là một vecto pháp tuyến của mặt phẳng (P)?

A. \[\overrightarrow {n_1^{}} (3;6;2)\]

B. \[\overrightarrow {n_3^{}} ( – 3;6;2)\]  

C. \[\overrightarrow {n_2^{}} (2;1;3)\]

D. \[\overrightarrow {n_4^{}} ( – 3;6; – 2)\]

Câu 11[TH]. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng \[\left( \alpha  \right)\]chứa trục Ox và đi qua điểm \[M(2; – 1;3)\]

A. \[(\alpha ): – y + 3z = 0\]                               

B. \[(\alpha ):2x – z + 1 = 0\]

C. \[(\alpha ):x + 2y + z – 3 = 0\]

D. \[(\alpha ):3y + z = 0\]

Câu 12[NB]. Hàm số f(x) nào dưới đây thỏa mãn \[\int {f(x)dx = \ln \left| {x + 3} \right| + C} \]?

A. \[f(x) = (x + 3)\ln (x + 3) – x\]

B. \[f(x) = \frac{1}{{x + 3}}\]                       

C. \[f(x) = \frac{1}{{x + 2}}\]                       

D. \[f(x) = \ln (\ln (x + 3))\]

Câu 13[VD]. Cho hình phẳng (H) giới hạn bởi đường cong \[y_{}^2 – 2y + x = 0\]và đường thẳng \[x + y – 2 = 0\] Tính diện tích S của hình (H)?

A.S = 6     

B.S = 14

C. \[S = \frac{{17}}{6}\]  

D. \[S = \frac{1}{6}\]

Câu 14[TH]. Cho số phức \[z = a + bi(a,b \in R)\]thỏa mãn \[(1 + i)z – \frac{{3 + 4i}}{{2 – i}} = (1 + i)_{}^2\]. Tính \[P = 10a + 10b.\]

A.- 42 

B.20

C.4     

D. 2

Câu 15[TH]. Tìm phần thực a của số phức \[z = i_{}^2 + … + i_{}^{2019}\]

A. a = 1     

B. \[a =  – 2_{}^{1009}\]

C. \[a = 2_{}^{1009}\]

D.  a= -1

Câu 16[VD]. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \[d_1^{}:\left\{ \begin{array}{l}x = 1 + t\\y = 0\\z =  – 5 + t\end{array} \right.\]và \[d_2^{}:\left\{ \begin{array}{l}x = 0\\y = 4 – 2t’\\z = 5 + 3t’\end{array} \right.\]. Viết phương trình đường vuông góc chung \[\Delta \]của d1, d2.

A. \[\Delta :\frac{x}{2} = \frac{{y – 4}}{{ – 3}} = \frac{{z – 5}}{{ – 2}}\]

B. \[\Delta :\frac{{x – 4}}{2} = \frac{y}{{ – 3}} = \frac{{z – 2}}{2}\]

C. \[\Delta :\frac{{x – 1}}{{22}} = \frac{y}{3} = \frac{{z + 5}}{2}\]

D. \[\Delta :\frac{{x – 4}}{{ – 2}} = \frac{y}{3} = \frac{{z + 2}}{2}\]

Câu 17[VD]. Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[A( – 3;5; – 5),B(5; – 3;7)\] và  mặt phẳng \[(P):x + y + z = 0\]. Tìm tọa độ của điểm M trên mặt phẳng (P) sao cho \[MA_{}^2 – 2MB_{}^2\]đạt giá trị lớn nhất.

  A. \[M( – 2;1;1)\]        B. \[M(2; – 1;1)\]       

  C. \[M(6; – 18;12)\]    D. \[M( – 6;18;12)\]

Câu 18[TH]. Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[M(3;0;0),N(2;2;2)\]. Mặt phẳng (P) thay đổi qua M, N cắt các trục Oy, Oz lần lượt tại B(0;b;0), C(0;0;c) (\[b,c \ne 0\])

A. b + c =6

B. bc = 3(b + c)

C. bc = b + c     

D. \[\frac{1}{b} + \frac{1}{c} = \frac{1}{6}\]

Câu 19[NB]. Cho \[I = \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{{\cot _{}^3x}}{{\sin _{}^2x}}dx} \] và u = cotx. Mệnh đê nào dưới đây đúng?

A. \[I = \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {u_{}^3du} \] 

B. \[I = \int\limits_0^1 {u_{}^3du} \]

C. \[I =  – \int\limits_0^1 {u_{}^3du} \]   

D. \[I = \int\limits_0^1 {udu} \]

Câu 20[TH]. Giả sử hàm số y = f(x) có đạo hàm liện tục trên [0;2] biết \[\int\limits_0^2 {f(x)dx = 8} \]. Tính \[\int\limits_0^3 {{\rm{[}}f(2 – x) + 1]dx} \].

A. -9       

B. 9

C. 10       

D. -6

Câu 21[TH]. Tìm các số thực x, y thỏa mãn \[(1 – 3i)x – 2y + (1 + 2y)i =  – 3 – 6i\]

A. \[x =  – 5,y =  – 4\] 

B. \[x = 5,y = 4\]       

C. \[x = 5,y =  – 4\]     

D. \[x =  – 5,y = 4\]

Câu 22[TH]. Gọi z1, z2 là hai nghiệm của phức của phương trình \[z_{}^2 + bz + c = 0(c \ne 0).\]Tính \[P = \frac{1}{{z_1^2}} + \frac{1}{{z_2^2}}\] theo b,c.

A. \[P = \frac{{b_{}^2 – 2c}}{c}\]. 

B. \[P = \frac{{b_{}^2 + 2c}}{{c_{}^2}}\] 

C. \[P = \frac{{b_{}^2 + 2c}}{c}\] 

D. \[P = \frac{{b_{}^2 – 2c}}{{c_{}^2}}\]

Câu 23[TH]. Tìm các giá trị thực của tham số m để số phức \[z = m_{}^3 + 3m_{}^2 – 4 + (m – 1)i\] là số thuần ảo.

A. \[\left[ \begin{array}{l}m = 1\\m =  – 2\end{array} \right.\] 

B. m = 1

C. m = – 2   

D.  m = 0

Câu 24[TH]. Trong mặt phẳng tọa độ, tập hợp điểm M(x,y) biểu diễn của số phức z = x+ yi  thỏa mãn \[\left| {z – 1 + 3i} \right| = \left| {z – 2 – i} \right|\] là

  A. Đường tròn đường kính AB với A(1;-3), B(2;1)

  B. Đường thẳng trung trực của đoạn thẳng AB với A(1;-3), B(2;1)

  C. Trung điểm của đoạn thẳng AB với A(1;-3), B(2;1)

  D. Đường thẳng trung trực của đoạn thẳng AB với A(-1;-3), B(-2;-1)

Câu 25[TH]. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[(S):(x + 3)_{}^2 + y_{}^2 + (z – 2)_{}^2 = m_{}^2 + 4\]. Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với (Oyz)

 A. m = 0     

B. m = 2; m = -2       

C. \[m = \sqrt 5 \] 

D. \[m = \sqrt 5 ,m =  – \sqrt 5 \]

Câu 26[TH]. Cho \[\int\limits_0^{\frac{\pi }{8}} {\cos _{}^22xdx}  = \frac{\pi }{a} + \frac{b}{c}\] với a, b, c là số nguyên dương, \[\frac{b}{c}\] tối giản. Tính P = a + b + c

A. P = 15                      B. P = 23

C. P = 24                      D. P = 25

Câu 27[TH]. Cho \[I = \int\limits_0^1 {\frac{{dx}}{{\sqrt {2x + a} }}} \], với a> 0 . Tìm a nguyên để \[I \ge 1\]

A. a = 1

B. a = 0                        

C. Vô số giá trị của a.  

D. Không có giá trị nào của a

Câu 28[TH]. Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm A’ đối xứng với điểm \[A( – 1;0;3)\]qua mặt phẳng \[(P):x + 3y – 2z – 7 = 0\]

A. \[A'( – 1; – 6;1)\]     B. \[A'(0;3;1)\]          

C. \[A'(1;6; – 1)\]        D. \[A'(11;0; – 5)\]

Câu 29[NB]. Tìm nguyên hàm của hàm số \[f(x) = 3_{}^x\]

A. \[\int {f(x)dx = \frac{{3_{}^x}}{{\ln 3}} + C} \]                            

B. \[\int {f(x)dx = \frac{{3_{}^{x + 1}}}{{x + 1}} + C} \]              

C. \[\int {f(x)dx = 3_{}^x + C} \]                  

D. \[\int {f(x)dx = 3_{}^x\ln 3 + C} \]

Câu 30[NB]. Số phức z = 4 – 3icó điểm biểu diễn là

A. M(4; 3)                    B. M(3; 4)

C. M(4; -3)                   D. M(-3; 4)

Câu 31[TH]. Tính \[I = \int\limits_{ – 1}^1 {\frac{{x_{}^3}}{{x_{}^2 + 2}}} dx\]

A. I = 1                        B. I = 0

C. I = 3                        D. I = -3

Câu 32[TH]. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[\Delta :\frac{{x – 3}}{2} = \frac{{y – 2}}{1} = \frac{z}{1}\] và mặt phẳng \[(\alpha ):3x + 4y + 5z + 8 = 0\]. Góc giữa đường thẳng \[\Delta \] và mặt phẳng \[(\alpha )\] có số đo là:

A. 450                          B. 900.

C. 300                          D. 600

Câu 33[NB]. Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu?

A. \[x_{}^2 + y_{}^2 + 2x – 4y + 10 = 0\]      

B. \[x_{}^2 + y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\]                     

C. \[x_{}^2 + 2y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\]                   

D. \[x_{}^2 – y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\]

Câu 34[VD]. Trong không gian với hệ tọa độ Oxyz, cho vật thế nằm giữa hai mặt phẳng x = 0 và x = 3. Biết rằng thiết diện của vật thế cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x\[(0 \le x \le 3)\]là một hình vuông cạnh là\[\sqrt {9 – x_{}^2} \]. Tính thể tích V của vật thể

A.V = 171                    B. \[V = 171\pi \]

C.  V = 18                    D. \[V = 18\pi \]

Câu 35[TH].Tìm số phức z thỏa mãn \[z + 2\overline z  = 2 – 4i\]

  A. \[z = \frac{2}{3} – 4i\] 

B. \[z =  – \frac{2}{3} + 4i\]  

C. \[z = \frac{2}{3} + 4i\] 

D. \[z =  – \frac{2}{3} – 4i\]

Câu 36[VD]. Biết \[\int {\frac{{(x – 1)_{}^{2016}}}{{(x + 2)_{}^{2018}}}} dx = \frac{1}{a}\left( {\frac{{x – 1}}{{x + 2}}} \right)_{}^b + C,x \ne  – 2\], với a, b nguyên dương. Mệnh đề nào dưới đây đúng?

A. a <  b   

B. a = b

C. a = 3b

D. b – a = 4034.

Câu 37[NB]. Trong không gian với hệ tọa độ Oxyz, cho \[\overrightarrow u  = 2\overrightarrow i  – 3\overrightarrow j  – \overrightarrow k \], tọa độ của \[\overrightarrow u \] là

  A. \[\overrightarrow u  = (2;3; – 1)\]   

B. \[\overrightarrow u  = (2; – 1;3)\] 

C. \[\overrightarrow u  = (2;3;1)\] 

D. \[\overrightarrow u  = (2; – 3; – 1)\]

Câu 38[NB]. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[\left\{ \begin{array}{l}x = t\\y = 1 – t\\z =  – 1 + 2t\end{array} \right.\] với mặt phẳng \[(\alpha ):x + 3y + z – 2 = 0\].Khẳng định nào sau đây là đúng?

  A. Đường thẳng d cắt mặt phẳng \[(\alpha )\]

  B. Đường thẳng d cắt mặt phẳng \[(\alpha )\]

  C. Đường thẳng d vuông góc với  mặt phẳng \[(\alpha )\]               

  D. Đường thẳng d song song với mặt phẳng \[(\alpha )\]

Câu 39[TH]. Cho hai hàm số\[F(x) = (x_{}^2 + ax + b)e_{}^x,f(x) = (x_{}^2 + 3x + 4)e_{}^x\]. Biết a, b là các số thực để F(x) là một nguyên hàm của f(x). Tính S = a+ b

A. S = – 6                     B. S = 12

C. S = 6                       D. S = 4

Câu 40[TH]. Cho hàm số f(x) xác định trên \[(e; + \infty )\]thỏa mãn \[f'(x) = \frac{1}{{x.\ln x}}\] và \[f(e_{}^2) = 0\]. Tính \[f(e_{}^4)\]

A. \[f(e_{}^4) = \ln 2\] 

B. \[f(e_{}^4) =  – \ln 2\]

C. \[f(e_{}^4) = 3\ln 2\]   

D. \[f(e_{}^4) = 2\]

Câu 41[VD]. Cho hình phẳng (H) (phần gạch chép trong hình vẽ). Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành

 

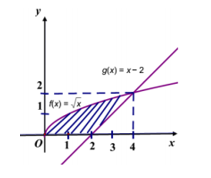
  A. \[V = 8\pi \]           B. \[V = 10\pi \]         

  C. \[V = \frac{{8\pi }}{3}\]                         D. \[V = \frac{{16\pi }}{3}\]

 

Câu 42[NB]. Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần tô đen trong hình vẽ) được tính theo công thức nào dưới đây?

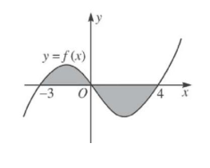
  A. \[S = \int\limits_{ – 3}^0 {f(x)dx}  – \int\limits_0^4 {f(x)dx} \]  

  B. \[S = \int\limits_{ – 3}^4 {f(x)dx} \]        

  C. \[S =  – \int\limits_{ – 3}^0 {f(x)dx}  + \int\limits_0^4 {f(x)dx} \]

  D. \[S = \int\limits_{ – 3}^1 {f(x)dx}  + \int\limits_1^4 {f(x)dx} \]

Câu 43[VD]. Tìm số thực m > 1 thỏa mãn \[\int\limits_1^m {x(2\ln x + 1)dx}  = 2m_{}^2\]

A. m = e                       B. m = 2

C. m = 0                       D. m = e2

Câu 44[NB]. Tập hợp các điểm biểu diễn của số phức z trên mặt phẳng tọa độ là đường tròn tâm I(0;1), bán kính R =3. Mệnh đề nào dưới đây là đúng?

A. \[\left| {z – 1} \right| = 3\] 

B. \[\left| {z – i} \right| = 3\]

C. \[\left| {z – i} \right| = \sqrt 3 \]   

D. \[\left| {z + i} \right| = 3\]

Câu 45[NB]. Phương trình nào dưới đây nhận được hai số phức  \[ – \sqrt 3 i\] và \[\sqrt 3 i\] là nghiệm?

A. \[z_{}^2 + 5 = 0\]    B. \[z_{}^2 + 3 = 0\] 

C. \[z_{}^2 + 9 = 0\]    D. \[z_{}^2 + \sqrt 3  = 0\]

Câu 46[VDC]. Cho hai số phức z1, z2 thỏa mãn \[\left| {z_1^{} – 1 + i} \right| = 1\] và \[z_2^{} = 2iz_1^{}\]. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = \left| {2z_1^{} – z_2^{}} \right|\]

A. \[P_{\min }^{} = 2 – \sqrt 2 \]   

B. \[P_{\min }^{} = 8 – \sqrt 2 \]     

C. \[P_{\min }^{} = 2 – 2\sqrt 2 \]       

D. \[P_{\min }^{} = 4 – 2\sqrt 2 \]

Câu 47[VD]. Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[A(3;2;1),M(3;0;0)\]và mặt phẳng \[(P):x + y + z – 3 = 0.\] Đường thẳng \[\Delta \] đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ điểm A đến đường thẳng \[\Delta \] là nhỏ nhất. Gọi vectơ \[\overrightarrow u (a,b,c)\]là một vectơ chỉ phương của \[\Delta \] (a, b, c là các số nguyên với ước chung lớn nhất là 1).

 Tính P = a + b + c

A. -1                            B. 1

C. 2                             D. 0

Câu 48[VD]. Cho hai số phức z1, z2 thỏa mãn \[\left| {z_1^{}} \right| = \sqrt 2 ,\left| {z_2^{}} \right| = 2.\]Gọi M, N lần lượt là các điểm biểu diễn của số phức z1, z2. Biết góc tạo bởi \[\overrightarrow {OM} ,\overrightarrow {ON} \]bằng 450. Tính giá trị biểu thức \[P = \left| {\frac{{z_1^{} + z_2^{}}}{{z_1^{} – z_2^{}}}} \right|\]

  A. \[P = \sqrt 5 \]   

B. \[P = \frac{1}{{\sqrt 5 }}\]                      

C. \[P = \frac{{2 + \sqrt 2 }}{{2 – \sqrt 2 }}\]

D. \[P = \frac{{2 + \sqrt 2 }}{{\sqrt 2  – 2}}\]

Câu 49[VDC]. Trong không gian với hệ tọa độ Oxyz,cho hai điểm \[M(1;0;2),N(1; – 1; – 1)\] và mặt phẳng \[(P):x + 2y – z + 2 = 0.\]Một mặt cầu đi qua M, N, tiếp xúc mặt phẳng (P) tại điểm E. Biết E luôn thuộc một đường tròn cố định, tìm bán kính của đường tròn đó.

A. \[R = \frac{{\sqrt {10} }}{2}\]     

B. \[R = \sqrt {10} \]

C.R= 10   

D. \[R = 2\sqrt 5 \]

Câu 50[VD]. Cho hàm số \[f(x)\]có đạo hàm liên tục trên R và thỏa mãn \[f(x) > 0,\forall x \in R\]. Biết f(0) =1 và \[f'(x) = (6x – 3x_{}^2)f(x)\].Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.

A. \[\left[ \begin{array}{l}m > e_{}^4\\0 < m < 1\end{array} \right.\] B. \[1 < m < e_{}^4\]

C. \[\left[ \begin{array}{l}m > e_{}^4\\m < 1\end{array} \right.\]     D. \[1 \le m \le e_{}^4\]

HƯỚNG DẪN GIẢI CHI TIẾT

1. A	2. A	3. C	4. B	5. A	6. B	7. B	8. B	9. D	10. A
11. D	12. B	13. D	14. D	15. D	16. D	17. C	18. D	19. B	20. C
21. B	22. D	23. A	24. B	25. D	26. D	27. D	28. C	29. A	30. C
31. B	32. D	33. B	34. C	35. C	36. C	37. D	38. B	39. D	40. A
41. D	42. A	43. D	44. B	45. B	46. D	47. D	48. A	49. D	50. A

Câu 1.

Giả sử \[z = a + bi,(a,b \in R)\]có điểm biểu diễn là M(a;b),

thỏa mãn điều kiện: \[\left| {z – (3 + 2i)} \right| = 2\]

Khi đó, \[\sqrt {(a – 3)_{}^2 + (b – 2)_{}^2}  = 2 \Leftrightarrow (a – 3)_{}^2 + (b – 2)_{}^2 = 2_{}^2\]                     

Vậy, tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(3;2), bán kính R = 2.

Chọn: A

Câu 2.

Phương pháp:

Đặt \[z = a + bi,(a,b \in R) \Rightarrow \overline z  = a – bi\]. Thay vào biểu thức và rút gọn.

Cách giải:

Giả sử \[z = a + bi,(a,b \in R)\]

Ta có

 \[\begin{array}{l}{\rm{w}} = \frac{{z_{}^2 – (\overline z )_{}^2}}{{1 + z.\overline z }}\\ = \frac{{(a_{}^2 – b_{}^2 + 2bi) – (a_{}^2 – b_{}^2 – 2bi)}}{{1 + a_{}^2 + b_{}^2}}\end{array}\]

\[ = \frac{{4bi}}{{1 + a_{}^2 + b_{}^2}}\] là số ảo

Chọn: A

Câu 3.

Phương pháp:

+ Giải phương trình bậc hai trên tập số phức.

+ \[z = a + bi,(a,b \in R) \Rightarrow \left| z \right| = \sqrt {a_{}^2 + b_{}^2} \]

Cách giải:

Ta có:

 \[\begin{array}{l}(z_{}^2 + z)_{}^2 + 4(z_{}^2 + z) – 12 = 0\\ \Leftrightarrow \left[ \begin{array}{l}z_{}^2 + z = 2\\z_{}^2 + z =  – 6\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}z_{}^2 + z – 2 = 0\\z_{}^2 + z + 6 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}z = 1\\z =  – 2\\z = \frac{{ – 1 + \sqrt {23} i}}{2}\\z = \frac{{ – 1 – \sqrt {23} i}}{2}\end{array} \right.\end{array}\]

\[\begin{array}{l}S = \left| {z_1^{}} \right|_{}^2 + \left| {z_2^{}} \right|_{}^2 + \left| {z_3^{}} \right|_{}^2 + \left| {z_4^{}} \right|_{}^2\\ = 1_{}^2 + 2_{}^2 + \frac{{1 + 23}}{4}.2 = 17\end{array}\]

Chọn: C

Câu 4.

Phương pháp:

Đường thẳng \[d:\left\{ \begin{array}{l}x = x_0^{} + at\\y = y_0^{} + bt\\z = z_0^{} + ct\end{array} \right.\] có một vectơ chỉ phương \[\overrightarrow u  = (a,b,c)\].

Cách giải:

Đường thẳng \[\left\{ \begin{array}{l}x = 1 – t\\y = 3\\z =  – 1 + 2t\end{array} \right.\] có một vectơ chỉ phương \[\overrightarrow u  = (1;0; – 2)\].

Chọn: B

Câu 5.

Mệnh đề sai: z là số thực.

Chọn: A

Câu 6.

Phương pháp:

Phương trình mặt cầu có tâm \[I(x_0^{};y_0^{},z_0^{})\], bán kính R:

\[(x – x_0^{})_{}^2 + (y – y_0^{})_{}^2 + (z – z_0^{})_{}^2 = R_{}^2\]

Cách giải:

Mặt cầu đường kính AB có tâm I(3;0;-1) là trung điểm của đoạn thẳng AB và bán kính \[R = \frac{{AB}}{2} = \frac{{\sqrt {0_{}^2 + 4_{}^2 + 2_{}^2} }}{2} = \sqrt 5 \], có phương trình \[(x – 3)_{}^2 + y_{}^2 + (z + 1)_{}^2 = 5\]

Chọn: B

Câu 7.

Phương pháp:

+) Gắn hệ trục tọa độ, lập phương trình đường parabol.

+) Tính diện tích của tấm cửa

Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), y = g(x), trục hoành và hai đường thẳng x =a; x = b được tính theo công thức \[S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx} \]

+) Tính chi phí làm cửa.

Cách giải:

Gắn hệ trục tọa độ như hình vẽ.

Giả sử phương trình đường Parabol là: \[y = ax_{}^2 + bx + c,a \ne 0(P)\]

Ta có:

 \[\begin{array}{l}\left\{ \begin{array}{l}0 = a( – 3)_{}^2 + b( – 3) + c\\0 = a.3_{}^2 + b.3 + c\\6 = c\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}9a – 3b + 6 = 0\\9a + 3b + 6 = 0\\c = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a =  – \frac{2}{3}\\b = 0\\c = 6\end{array} \right.\end{array}\]

\[ \Rightarrow (P);y =  – \frac{2}{3}x_{}^2 + 6\]

Diện tích làm cửa là:

 \[\begin{array}{l}S = \int\limits_{ – 3}^3 {\left( { – \frac{2}{3}x_{}^2 + 6} \right)dx} \\ = \left. {\left( { – \frac{2}{9}x_{}^3 + 6x} \right)} \right|_{ – 3}^3\\ = ( – 6 + 18) – (6 – 18) = 24(m_{}^2)\end{array}\]

Chi phí làm cửa là: \[24 \times 800{\rm{ 000  =  19 200 000}}\](đồng)

Chọn: B

Câu 8.

Phương pháp:

Phương trình mặt phẳng đi qua M0(x0; y0; z0) có 1 VTPT \[\overrightarrow n  = (a,b,c) \ne \overrightarrow 0 \]

                                    \[a(x – x_0^{}) + b(y – y_0^{}) + c(z – z_0^{}) = 0\]

Cách giải:

\[(P):2x – z + 1 = 0\] có 1 VTPT \[\overrightarrow {n_1^{}}  = (2;0; – 1)\]

\[(Q):y – 2 = 0.\] có 1 VTPT \[\overrightarrow {n_2^{}}  = (0;1;0)\]

Do \[(\alpha )\] vuông góc với hai mặt phẳng (P), (Q) nên \[(\alpha )\] có 1 VTPT \[\overrightarrow n  = \left[ {\overrightarrow {n_1^{}} ,\overrightarrow {n_2^{}} } \right] = (1;0;2)\]

Phương trình mặt phẳng \[(\alpha )\] là: \[1(x – 2) + 0 + 2(z – 1) = 0 \Leftrightarrow x + 2z – 4 = 0\]

Chọn: B

Câu 9.

Phương pháp:

Tập hợp các điểm M cách đều ba điểm A, B, C (A, B, C không thẳng hàng) là đường thẳng vuông góc với (ABC)tại tâm đường tròn ngoại tiếp \[\Delta ABC\]

Cách giải:

Ta có: \[A(0;0;1),B( – 1; – 2;0),C(2;0; – 1) \Rightarrow \overrightarrow {AB}  = ( – 1; – 2; – 1),\overrightarrow {AC}  = (2;0; – 2)\]

\[ \Rightarrow A,B,C\] không thẳng hàng.

Nhận xét: Tập hợp các điểm M cách đều ba điểm A, B, C (A, B, C không thẳng hàng) là đường thẳng vuông góc với (ABC) tại tâm đường tròn ngoại tiếp \[\Delta ABC\]

Mặt phẳng (ABC) có 1 VTPT là \[\overrightarrow n  = \frac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (1; – 1;1)\]có phương trình là:

\[1(x – 0) – 1(y – 0) + 1(z – 1) = 0 \Leftrightarrow x – y + z – 1 = 0\]

Gọi I(a,b,c) là tâm đường tròn ngoại tiếp \[\Delta ABC\]

\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}a – b + c – 1 = 0\\IA_{}^2 = IB_{}^2\\IA_{}^2 = IC_{}^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a – b + c – 1 = 0\\a_{}^2 + b_{}^2 + (c – 1)_{}^2 = (a – 1)_{}^2 + (b + 2)_{}^2 + c_{}^2\\a_{}^2 + b_{}^2 + (c – 1)_{}^2 = (a – 2)_{}^2 + b_{}^2 + (c + 1)_{}^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a – b + c – 1 = 0\\a + 2b + c + 2 = 0\\a – c = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b =  – 1\\c =  – \frac{1}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{1}{2}; – 1; – \frac{1}{2}} \right)\end{array}\]

\[\Delta \] đi qua \[I\left( {\frac{1}{2}; – 1; – \frac{1}{2}} \right)\] và có 1 VTCP \[(1; – 1;1)\], có phương trình \[\Delta :\left\{ \begin{array}{l}x = \frac{1}{2} + t\\y =  – 1 – t\\z =  – \frac{1}{2} + t\end{array} \right.\]

Chọn: D

Câu 10.

\[(P):\frac{x}{2} + \frac{y}{1} + \frac{z}{3} = 1 \Leftrightarrow 3x + 6y + 2z – 6 = 0\] có 1 VTPT \[\overrightarrow {n_1^{}}  = (3;6;2)\]

Chọn: A

Câu 11.

Phương pháp:

Phương trình mặt phẳng đi qua M0(x0; y0; z0) có 1 VTPT \[\overrightarrow n  = (a,b,c) \ne \overrightarrow 0 \]

                                    \[a(x – x_0^{}) + b(y – y_0^{}) + c(z – z_0^{}) = 0\]

Cách giải:

Mặt phẳng \[(\alpha )\] có 1 VTPT \[\overrightarrow n  = \left[ {\overrightarrow i ;\overrightarrow {OM} } \right] = (0; – 3; – 1)\] có phương trình là

                                    \[0 – 3(y – 0) – 1(z – 0) = 0 \Leftrightarrow 3y + z = 0\]

Chọn: D

Câu 12.

Phương pháp:

\[\int {f(x)dx = F(x) \Rightarrow f(x) = F'(x)} \]

Cách giải:

\[\begin{array}{l}\int {f(x)dx = \ln \left| {x + 3} \right|}  + C\\ \Rightarrow f(x) = \left( {\ln \left| {x + 3} \right| + C} \right)’ = \frac{1}{{x + 3}}\end{array}\]

Chọn: B

Câu 13.

Phương pháp:

Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), y = g(x), trục hoành và hai đường thẳng x =a; x = b được tính theo công thức \[S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx} \]

Cách giải:

Ta có:

 \[\begin{array}{l}y_{}^2 – 2y + x = 0 \Leftrightarrow x =  – y_{}^2 + 2y;\\x + y – 2 = 0 \Leftrightarrow x = 2 – y\end{array}\]

Giải phương trình \[ – y_{}^2 + 2y = 2 – y \Leftrightarrow \left[ \begin{array}{l}y = 1\\y = 2\end{array} \right.\]

Diện tích cần tìm là:

\[\begin{array}{l}S = \int\limits_1^2 {\left| {( – y_{}^2 + 2y) – (2 – y)} \right|dy}  = \int\limits_1^2 {\left| {( – y_{}^2 + 3y – 2)} \right|dy} \\{\rm{    = }}\int\limits_1^2 {( – y_{}^2 + 3y – 2)dy}  = \left. {\left( { – \frac{1}{3}y_{}^3 + \frac{3}{2}y_{}^2 – 2y} \right)} \right|_1^2\\{\rm{    = }}\left( { – \frac{8}{3} + 6 – 4} \right) – \left( { – \frac{1}{3} + \frac{3}{2} – 2} \right) = \frac{1}{6}\end{array}\]

Chọn: D

Câu 14.

Phương pháp:

Áp dụng quy tắc nhân, chia số phức.

Cách giải:

Ta có:

\[\begin{array}{l}(1 + i)z – \frac{{3 + 4i}}{{2 – i}} = (1 – i)_{}^2\\ \Leftrightarrow (1 + i)z – \frac{{(3 + 4i)(2 + i)}}{5} =  – 2i\\ \Leftrightarrow (1 + i)z – \frac{{2 + 11i}}{5} =  – 2i\\ \Leftrightarrow (1 + i)z =  – 2i + \frac{{2 + 11i}}{5}\\ \Leftrightarrow (1 + i)z = \frac{{2 + i}}{5}\\ \Leftrightarrow z = \frac{{2 + i}}{{5(1 + i)}}\\ \Leftrightarrow z = \frac{{(2 + i)(1 – i)}}{{5.2}}\\ \Leftrightarrow z = \frac{3}{{10}} – \frac{1}{{10}}i\\ \Rightarrow \left\{ \begin{array}{l}a = \frac{3}{{10}}\\b =  – \frac{1}{{10}}\end{array} \right.\\ \Rightarrow P = 10a + 10b = 2\end{array}\]

Chọn: D

Câu 15.

Phương pháp:

\[i_{}^n = \left\{ \begin{array}{l}1,n = 4k,k \in N\\i,n = 4k + 1,k \in N\\ – 1,n = 4k + 2,k \in N\\ – i,n = 4k + 3,k \in N\end{array} \right.\]

Cách giải:

Nhận xét: Tổng của 4 số hạng liên tiếp trong biểu thức đều bằng 0.

Tổng \[z = i_{}^2 + … + i_{}^{2019}\] có 2018 số hạng (2018 = 4.504 +2)

nên \[z = i_{}^2 + … + i_{}^{2019} = i_{}^2 + i_{}^3 + (i_{}^4 + … + i_{}^{2019}) = i_{}^2 + i_{}^3 + 0 =  – 1 – i\]

Phần thực của số phức z là: -1

Chọn: D

Câu 16.

Phương pháp:

Tham số hóa hai giao điểm của Dvới d1, d2. Tìm tọa độ 2 giao điểm này

Viết phương trình đường thẳng D

Cách giải:

Gọi A, B lần lượt là giao điểm của Dvới d1, d2.

Giả sử \[A(1 + t;0; – 5 + t),B(0;4 – 2t’;5 + 3t’)\]

\[ \Rightarrow \overrightarrow {AB}  = ( – 1 – t;4 – 2t’;10 + 3t’ – t)\]

Do Dlà đường vuông góc chung của d1, d2 nên

\[\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {u_{d_1^{}}^{}}  = 0\\.\overrightarrow {AB} .\overrightarrow {u_{d_2^{}}^{}}  = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}( – 1 – t).1 + 0 + (10 + 3t’ – t).1 = 0\\0 – 2(4 – 2t’) + 3(10 + 3t’ – t) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}t’ =  – 1\\t = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A(4;0; – 4)\\\overrightarrow {AB}  = ( – 4;6;4)\end{array} \right.\end{array}\]

Đường thẳng D đi qua \[A(4;0; – 4)\] và có 1 VTCP \[\overrightarrow u  = \frac{1}{2}\overrightarrow {AB}  = ( – 2;3;2)\], có phương trình

  \[\Delta :\frac{{x – 4}}{{ – 2}} = \frac{y}{3} = \frac{{z + 2}}{2}\]

Chọn: D

Câu 17.

Phương pháp:

Xác định điểm I thỏa mãn \[\overrightarrow {IA}  – 2\overrightarrow {IB}  = \overrightarrow 0 \]

Cách giải:

Lấy I(a,b,c) thỏa mãn \[\overrightarrow {IA}  – 2\overrightarrow {IB}  = \overrightarrow 0 \]

\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} – 3 – a = 2(5 – a)\\5 – b = 2( – 3 – b)\\ – 5 – c = 2(7 – c)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 13\\b =  – 11\\c = 19\end{array} \right.\end{array}\]

Khi đó,

\[\begin{array}{l}MA_{}^2 – 2MB_{}^2 = \overrightarrow {MA} _{}^2 – \overrightarrow {MB} _{}^2\\ = (\overrightarrow {MI}  + \overrightarrow {IA} )_{}^2 – 2(\overrightarrow {MI}  + \overrightarrow {IB} )_{}^2\\ =  – \overrightarrow {MI} _{}^2 + 2\overrightarrow {MI} (\overrightarrow {IA}  – 2\overrightarrow {IB} ) + IA_{}^2 – 2IB_{}^2\\ =  – MI_{}^2 + IA_{}^2 – 2IB_{}^2\end{array}\]

\[(MA_{}^2 – 2MB_{}^2)_{\max }^{} \Leftrightarrow MI_{\min }^{} \Leftrightarrow \]M là hình chiếu của I lên (P)

Phương trình đường thẳng d đi qua I vuông góc với (P) là: \[\left\{ \begin{array}{l}x = 13 + t\\y =  – 11 + t\\z = 19 + t\end{array} \right.\]

Giả sử \[M(13 + t; – 11 + t;19 + t)\].

 Mà \[M \in (P) \Rightarrow 13 + t + ( – 11 + t) + 19 + t = 0 \Leftrightarrow t =  – 7 \Rightarrow M(6; – 18;12)\]

Chọn: C

Câu 18.

Phương pháp:

Phương trình mặt phẳng (P) cắt Ox, Oy, Oz lần lượt tại các điểm \[A(a;0;0),B(0;b;0),C(0;0;c),(a,b,c \ne 0)\] là: \[\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\]

Cách giải:

 (P) đi qua các điểm \[M(3;0;0),{\rm{ }}B(0;b;0),{\rm{ }}C(0;0;c),{\rm{ }}(b,c \ne 0)\]

 Phương trình mặt phẳng (P) là: \[\frac{x}{3} + \frac{y}{b} + \frac{z}{c} = 1\]

Do N(2;2;2) \[ \in (P)\]

\[\begin{array}{l} \Rightarrow \frac{2}{3} + \frac{2}{b} + \frac{2}{c} = 1\\ \Leftrightarrow \frac{2}{b} + \frac{2}{c} = \frac{1}{3} \Leftrightarrow \frac{1}{b} + \frac{1}{c} = \frac{1}{6}\end{array}\]

Chọn: D

Câu 19.

Phương pháp:

Đặt u = cot x

Cách giải:

 Đặt \[u = \cot x \Rightarrow du = \frac{{ – 1}}{{\sin _{}^2x}}dx\]

Đổi cận: \[x = \frac{\pi }{4} \to t = 1;x = \frac{\pi }{2} \to t = 0\]

\[I = \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{{\cot _{}^3x}}{{\sin _{}^2x}}dx}  =  – \int\limits_1^0 {u_{}^3du}  = \int\limits_0^1 {u_{}^3du} \]

Chọn: B

Câu 20.

Phương pháp:

Đặt t = 2- x

Cách giải:

 Đặt \[t = 2 – x \Rightarrow dt =  – dx\]

Đổi cận: \[x = 0 \to t = 2;x = 2 \to t = 0\]

Khi đó

 \[\begin{array}{l}I = \int\limits_0^2 {f(x)dx} \\ = \int\limits_2^0 {f(2 – t)( – dt)} \\ = \int\limits_0^2 {f(2 – t)dt = 8} \\ \Rightarrow \int\limits_0^2 {f(2 – x)dx = 8} \end{array}\]

\[\int\limits_0^2 {\left[ {f(2 – x) + 1} \right]dx = \int\limits_0^2 {f(2 – x)dx + \int\limits_0^2 {1dx = 8 + \left. x \right|_0^2 = 8 + 2 = 10} } } \]

Chọn: C

Câu 21.

Phương pháp:

Hai số phức \[z = z’ \Leftrightarrow \left\{ \begin{array}{l}a = a’\\b = b’\end{array} \right.,\]với \[z = a + bi,z’ = a’ + b’i,(a,a’,b,b’ \in R)\]

Cách giải:

 Ta có

\[\begin{array}{l}(1 – 3i)x – 2y + (1 + 2y)i =  – 3 – 6i\\ \Leftrightarrow (x – 2y) + ( – 3x + 1 + 2y)i =  – 3 – 6i\\ \Leftrightarrow \left\{ \begin{array}{l}x – 2y =  – 3\\ – 3x + 1 + 2y =  – 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x – 2y =  – 3\\ – 3x + 2y =  – 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 4\end{array} \right.\end{array}\]

Chọn: B

Câu 22.

Phương pháp:

Sử dụng định lí Vi – ét:

Nếu z1, z2 là hai nghiệm phức của phương trình \[az_{}^2 + bz + c = 0,(a \ne 0)\]thì

\[z_1^{} + z_2^{} =  – \frac{b}{a}\& z_1^{}z_2^{} = \frac{c}{a}\]

Cách giải:

z1, z2 là hai nghiệm phức của phương trình \[z_{}^2 + bz + c = 0,(c \ne 0) \Rightarrow \left\{ \begin{array}{l}z_1^{} + z_2^{} =  – b\\z_1^{}z_2^{} = c\end{array} \right.\]

\[\begin{array}{l}P = \frac{1}{{z_1^2}} + \frac{1}{{z_2^2}} = \frac{{z_1^2 + z_2^2}}{{z_1^2z_2^2}}\\ = \frac{{(z_1^2 + z_2^2)_{}^2 – 2z_1^{}z_2^{}}}{{z_1^2z_2^2}}\\ = \frac{{b_{}^2 – 2c}}{{c_{}^2}}\end{array}\]

Chọn: D

Câu 23.

Phương pháp:

Số phức z = a+ bi \[(a,b \in R)\]là số thuần ảo \[ \Leftrightarrow a = 0\]

Cách giải:

Số phức \[z = m_{}^3 + 3m_{}^2 – 4 + (m – 1)i\] là số thuần ảo

 \[ \Leftrightarrow m_{}^3 + 3m_{}^2 – 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  – 2\end{array} \right.\]

Chọn: A

Câu 24.

Phương pháp:

Tập hợp các điểm biểu diễn số phức z thỏa mãn

\[\left| {z – (a + bi)} \right| = \left| {z – (a’ + b’i)} \right|,(a,b,a’,b’ \in R)\]là đường trung trực của đoạn thẳng AA’ với A(a,b), A’(a’,b’).

Cách giải:

Ta có

 \[\begin{array}{l}\left| {z – 1 + 3i} \right| = \left| {z – 2 – i} \right|\\ \Leftrightarrow \sqrt {(x – 1)_{}^2 + (y + 3)_{}^2}  = \sqrt {(x – 2)_{}^2 + (y – 1)_{}^2} \end{array}\]

\[ \Rightarrow \] Tập hợp điểm M biểu diễn số phức z= x +yi \[(x,y \in R)\] là đường trung trực của đoạn thẳng AB với A(1;-3), B(2;1).

Chọn: B

Câu 25.

Phương pháp:

Mặt cầu (S)tâm I, bán kính R tiếp xúc với mặt phẳng (P) khi và chỉ khi d(I;(P)) = R

Cách giải:

Mặt cầu (S):  \[(x + 3)_{}^2 + y_{}^2 + (z – 2)_{}^2 = m_{}^2 + 4\]có tâm \[I( – 3;0;2)\], bán kính \[R = \sqrt {m_{}^2 + 4} \]

Mặt cầu (S) tiếp xúc với (Oyz)

\[\begin{array}{l} \Leftrightarrow d(I;(Oyz)) = R \Leftrightarrow 3 = \sqrt {m_{}^2 + 4} \\ \Leftrightarrow m_{}^2 + 4 = 9 \Leftrightarrow m_{}^2 = 5 \Leftrightarrow m =  \pm \sqrt 5 \end{array}\]

Chọn: D

Câu 26.

Phương pháp:

Sử dụng công thức hạ bậc \[\cos _{}^2x = \frac{{1 + \cos 2x}}{2}\]sau đó sử dụng các công thức tính nguyên hàm cơ bản

Cách giải:

Ta có:

\[\begin{array}{l}\int\limits_0^{\frac{\pi }{8}} {\cos _{}^22xdx}  = \frac{1}{2}\int\limits_0^{\frac{\pi }{8}} {(1 + \cos 4x)dx} \\ = \left. {\frac{1}{2}\left( {x + \frac{1}{4}\sin 4x} \right)} \right|_0^{\frac{\pi }{8}}\\{\rm{ = }}\frac{1}{2}.\frac{\pi }{8} + \frac{1}{8}\sin \frac{\pi }{2}\\ = \frac{\pi }{{16}} + \frac{1}{8} = \frac{\pi }{a} + \frac{b}{c}\\ \Rightarrow a = 16,b = 1,c = 8\\ \Rightarrow P = a + b + c = 25.\end{array}\]

Chọn: D

Câu 27.

Phương pháp:

Sử dụng công thức nguyên hàm \[I = \int {\frac{{dx}}{{\sqrt x }} = 2\sqrt x  + C} \]

Cách giải:

Ta có

\[\begin{array}{l}I = \int\limits_0^1 {\frac{{dx}}{{\sqrt {2x + a} }}}  = \frac{1}{2}\int\limits_0^1 {\frac{{d(2x + a)}}{{\sqrt {2x + a} }}} \\ = \left. {\frac{1}{2}2\sqrt {2x + a} } \right|_0^1 = \left. {\sqrt {2x + a} } \right|_0^1\\ = \sqrt {2 + a}  – \sqrt a \end{array}\]

Để \[I \ge 1\] thì \[\sqrt {2 + a}  – \sqrt a  \ge 1\]

\[\begin{array}{l} \Leftrightarrow \sqrt {2 + a}  \ge \sqrt a  + 1\\ \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\2 + a \ge a + 2\sqrt a \end{array} \right.\end{array}\]

\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\1 \ge 2\sqrt a \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\\sqrt a  \le \frac{1}{2}\end{array} \right.\\ \Leftrightarrow 0 \le a \le \frac{1}{4}\end{array}\]

Mà \[a \in \mathbb{Z},a > 0 \Rightarrow a \in \emptyset \]

Chọn: D

Câu 28.

Phương pháp:

Giả sử A’(a,b,c) là điểm đối xứng với điểm A qua mặt phẳng (P). Khi đó, ta có: \[\left\{ \begin{array}{l}\overrightarrow {{\rm{AA}}’} //\overrightarrow {n_{(P)}^{}} \\I \in (P)\end{array} \right.\], với I là trung điểm của AA’

Cách giải:

Giả sử A’(a,b,c) là điểm đối xứng với điểm A(-1;0;3) qua mặt phẳng (P): x + 3y – 2z – 7 = 0

Khi đó, ta có: \[\left\{ \begin{array}{l}\overrightarrow {{\rm{AA}}’} //\overrightarrow {n_{(P)}^{}} \\I \in (P)\end{array} \right.\], với I là trung điểm AA’

\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\frac{{a + 1}}{1} = \frac{{b – 0}}{3} = \frac{{c – 3}}{{ – 2}}\\\left( {\frac{{a – 1}}{2}} \right) + 3.\frac{b}{2} – 2.\frac{{c + 3}}{2} – 7 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{{a + 1}}{1} = \frac{b}{3} = \frac{{c – 3}}{{ – 2}}\\a + 3b – 2c = 21\end{array} \right.\\ \Rightarrow \frac{{a + 1}}{1} = \frac{b}{3} = \frac{{c – 3}}{{ – 2}}\\ = \frac{{a + 1 + 3b – 2c + 6}}{{1 + 9 + 4}}\\ = \frac{{21 + 1 + 6}}{{14}} = 2\\ \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 6\\c =  – 1\end{array} \right. \Rightarrow A'(1;6; – 1)\end{array}\]

Chọn: C

Câu 29.

f(x) = 3x \[ \Rightarrow \int {f(x)dx = \frac{{3_{}^x}}{{\ln 3}} + C} \]

Chọn: A

Câu 30.

Phương pháp:

 Số phức z = a + bi có điểm biểu diễn là: M(a;b)

Cách giải:

Số phức z = 4 – 3i có điểm biểu diễn là: M(-3; 4)

Chọn: D

Câu 31.

Phương pháp:

f(x) là hàm số lẻ \[ \Rightarrow I = \int\limits_{ – a}^a {f(x)dx = 0} \]

Cách giải:

Đặt t = – x \[ \Rightarrow dt =  – dx\]. Đổi cận \[\left\{ \begin{array}{l}x = 1 \to t =  – 1\\x =  – 1 \to t = 1\end{array} \right.\]

\[\begin{array}{l}I = \int\limits_1^{ – 1} {\frac{{ – t_{}^3}}{{t_{}^2 + 2}}( – dt) = } \int\limits_{ – 1}^1 {\frac{{ – t_{}^3}}{{t_{}^2 + 2}}dt} \\ – \int\limits_{ – 1}^1 {\frac{{t_{}^3}}{{t_{}^2 + 2}}dt = }  – I \Leftrightarrow I = 0\end{array}\]

Chọn: B

Câu 32.

Đường thẳng \[\Delta \] có t VTCP là \[\overrightarrow u (2;1;1)\], mặt phẳng \[(\alpha )\]có 1 VTPT là \[\overrightarrow n (3,4,5)\]

Gọi \[\varphi \] là góc giữa đường thẳng \[\Delta \] và mặt phẳng \[(\alpha )\], khi đó

  \[\begin{array}{l}\sin \varphi  = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow n } \right|}}\\ = \frac{{\left| {2.3 + 1.4 + 1.5} \right|}}{{\sqrt {2_{}^2 + 1_{}^2 + 1_{}^2} .\sqrt {3_{}^2 + 4_{}^2 + 5_{}^2} }}\\ = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi  = 60_{}^0\end{array}\]

Chọn: D

Câu 33.

Phương pháp:

Phương trình mặt cầu có dạng \[x_{}^2 + y_{}^2 + z_{}^2 – 2ax – 2by – 2cz + d = 0\]với

\[a_{}^2 + b_{}^2 + c_{}^2 – d > 0\]

Cách giải:

Nhận xét \[x_{}^2 + y_{}^2 + 2x – 4y + 10 = 0\], \[x_{}^2 + 2y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\],

vaf \[x_{}^2 – y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\] không phải là phương trình mặt cầu. 

\[x_{}^2 + y_{}^2 + z_{}^2 + 2x – 2y – 2z – 2 = 0\] có: \[a_{}^2 + b_{}^2 + c_{}^2 – d = 1 + 1 + 1 – ( – 2) > 0\]

=> Đây là phương trình mặt cầu.

Chọn: B

Câu 34.

Thể tích cần tìm là:

 \[\begin{array}{l}V = \int\limits_0^3 {S(x)dx} \\ = \int\limits_0^3 {(9 – x_{}^2)dx}  = \left. {\left( {9x – \frac{1}{3}{x^3}} \right)} \right|_0^3\\ = (27 – 9) – 0 = 18\end{array}\].

Chọn: C

Câu 35.

Đặt \[z = a + bi,(a,b \in R) \Rightarrow \overline z  = a – bi\].

Ta có

 \[\begin{array}{l}z + 2\overline z  = 2 – 4i\\ \Leftrightarrow a + bi + 2(a – bi) = 2 – 4i\\ \Leftrightarrow 3a – bi = 2 – 4i\\ \Leftrightarrow \left\{ \begin{array}{l}3a = 2\\ – b =  – 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{2}{3}\\b = 4\end{array} \right. \Rightarrow z = \frac{2}{3} + 4i\end{array}\]

Chọn: C

Câu 36.

Phương pháp:

Đặt \[t = \frac{{x – 1}}{{x + 2}}\].

Cách giải:

Ta có : . \[\left( {\frac{{x – 1}}{{x + 2}}} \right)’ = \frac{3}{{(x + 2)_{}^2}}\]

Khi đó:\[\int {\frac{{(x + 1)_{}^{2016}}}{{(x + 2)_{}^{2018}}}} dx = \int {\left( {\frac{{x – 1}}{{x + 2}}} \right)_{}^{2016}.\frac{1}{{(x + 2)_{}^2}}dx} \]

Đặt \[t = \frac{{x – 1}}{{x + 2}}\]

\[\begin{array}{l} \Rightarrow dt = \frac{3}{{(x + 2)_{}^2}}dx\\ \Leftrightarrow \frac{{dx}}{{(x + 2)_{}^2}} = \frac{{dt}}{3}\end{array}\]

\[\begin{array}{l} \Rightarrow \int {\frac{{(x + 1)_{}^{2016}}}{{(x + 2)_{}^{2018}}}} dx = \int {t_{}^{2016}} \frac{{dt}}{3}\\ = \frac{1}{3}\frac{{t_{}^{2017}}}{{2017}} + C\\ = \frac{1}{{6051}}\left( {\frac{{x – 1}}{{x + 2}}} \right)_{}^{2017} + C\\ \Rightarrow a = 6051,b = 2017\\ \Rightarrow a = 3b\end{array}\]

Chọn: C

Câu 37.

\[\overrightarrow u  = 2\overrightarrow i  – 3\overrightarrow {\rm{j}}  – \overrightarrow k  \Leftrightarrow \overrightarrow u  = (2, – 3, – 1)\]

Chọn: D

Câu 38.

Phương pháp:

Kiểm tra mối quan hệ giữa VTCP của d và VTPT của (P).

Cách giải:

Đường thẳng \[\left\{ \begin{array}{l}x = t\\y = 1 – t\\z =  – 1 + 2t\end{array} \right.\]có 1 VTCP là \[\overrightarrow u  = (1, – 1,2)\]

Mặt phẳng \[(\alpha ):x + 3y + z – 2 = 0\] có 1 VTPT là \[\overrightarrow n  = (1,3,1)\]

Ta có: \[\overrightarrow u .\overrightarrow n  = 1 – 3 + 2 = 0 \Rightarrow \overrightarrow u  \bot \overrightarrow n  \Rightarrow \left\{ \begin{array}{l}d//(\alpha )\\d \subset (\alpha )\end{array} \right.\]

Lấy \[A(0;1; – 1) \in d,\]ta có \[(\alpha ):0 + 3.1 + ( – 1) – 2 = 0\]: đúng\[ \Rightarrow A \in (\alpha ) \Rightarrow \]Đường thẳng d nằm trên mặt phẳng (a)

Chọn: B

Câu 39.

Phương pháp:

\[F(x) = \int {f(x)dx \Rightarrow F'(x) = f(x)} \]

Cách giải:

F(x) là một nguyên hàm của f(x) \[ \Rightarrow F'(x) = f(x)\]

\[\begin{array}{l}\left( {(x_{}^2 + ax + b)e_{}^x} \right)’ = (x_{}^2 + 3x + 4)e_{}^x\\ \Leftrightarrow (2x + a)e_{}^x + (x_{}^2 + ax + b)e_{}^x = (x_{}^2 + 3x + 4)e_{}^x\end{array}\]

\[\begin{array}{l} \Leftrightarrow (x_{}^2 + (a + 2)x + a + b)e_{}^x = (x_{}^2 + 3x + 4)e_{}^x,\forall x\\ \Rightarrow \left\{ \begin{array}{l}a + 2 = 3\\a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 3\end{array} \right. \Rightarrow S = a + b = 4\end{array}\]

Chọn: D

Câu 40.

Phương pháp:

Tích phân hai vế \[f'(x) = \frac{1}{{x.\ln x}}\], lấy cận e2, e4.

Cách giải:

\[\begin{array}{l}f'(x) = \frac{1}{{x.\ln x}}\\ \Rightarrow \int\limits_{e_{}^2}^{e_{}^4} {f'(x)dx = \int\limits_{e_{}^2}^{e_{}^4} {\frac{1}{{x.\ln x}}dx \Leftrightarrow f(e_{}^4) – f(e_{}^2) = } } \int\limits_{e_{}^2}^{e_{}^4} {\frac{1}{{\ln x}}dx} (\ln x)\\ \Leftrightarrow f(e_{}^4) – 0 = \ln \left. {\left| {\ln x} \right|} \right|_{e_{}^2}^{e_{}^4}\\ \Leftrightarrow f(e_{}^4) = \ln 4 – \ln 2\\ \Leftrightarrow f(e_{}^4) = \ln 2\end{array}\]

Chọn: A

Câu 41.

Phương pháp:

Cho hai hàm số y=f(x) và y = g(x)  liên tục trên [a; b]. Khi đó thể tích vật thể tròn xoay giới hạn bởi hai đồ thị hàm số y=f(x) và y = g(x)  và hai đường thẳng x = a; y = b khi quay quanh trục Ox là:

  \[V = \pi \int\limits_a^b {\left| {f_{}^2(x) – g_{}^2(x)} \right|dx} \]

Cách giải:

Thể tích cần tìm là:

\[\begin{array}{l}V = \pi \int\limits_0^2 {(\sqrt x )_{}^2dx + \pi \int\limits_2^4 {\left[ {(\sqrt x )_{}^2 – (x – 2)_{}^2} \right]} } \\ = \pi \int\limits_0^2 {xdx}  + \pi \int\limits_2^4 {\left[ { – x_{}^2 + 5x – 4} \right]dx} \\ = \left. {\frac{1}{2}\pi x_{}^2} \right|_0^2 + \pi \left. {\left( { – \frac{1}{3}x_{}^3 + \frac{5}{2}x_{}^2 – 4x} \right)} \right|_2^4\\ = 2\pi  + \pi \left[ {\left( { – \frac{{64}}{3} + 40 – 16} \right) – \left( { – \frac{8}{3} + 10 – 8} \right)} \right]\\ = \frac{{16}}{3}\pi \end{array}\]

Chọn: D

Câu 42.

\[S = \int\limits_{ – 3}^0 {\left| {f(x)} \right|dx = } \int\limits_{ – 3}^0 {f(x)dx – \int\limits_0^4 {f(x)dx} } \]

Chọn: A

Câu 43.

Phương pháp:

Sử dụng công thức tích phân từng phần \[\int\limits_a^b {udv}  = \left. {uv} \right|_a^b – \int\limits_a^b {vdu} \]

Cách giải:

\[\begin{array}{l}\int\limits_1^m {x(2\ln x + 1)dx}  = \frac{1}{2}\int\limits_1^m {(2\ln x + 1)d(x_{}^2)} \\ = \left. {\frac{1}{2}(2\ln x + 1)x_{}^2} \right|_1^m – \frac{1}{2}\int\limits_1^m {(x_{}^2)d(2\ln x + 1)} \\ = \frac{1}{2}\left( {(2\ln m + 1)m_{}^2 – 1} \right) – \frac{1}{2}\int\limits_1^m {x_{}^2\frac{2}{x}dx} \\ = \frac{1}{2}(2m_{}^2\ln m + m_{}^2 – 1) – \int\limits_1^m {xdx} \\ = \frac{1}{2}(2m_{}^2\ln m + m_{}^2 – 1) – \left. {\frac{1}{2}x_{}^2} \right|_1^m\\ = \frac{1}{2}(2m_{}^2\ln m + m_{}^2 – 1) – \frac{{m_{}^2}}{2} + \frac{1}{2}\\ = m_{}^2\ln m\end{array}\]

Mà \[\int\limits_1^m {x(2\ln x + 1)dx}  = 2m_{}^2 \Rightarrow m_{}^2\ln m = 2m_{}^2\]

\[ \Leftrightarrow m_{}^2(\ln m – 2) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0(L)\\\ln m = 2\end{array} \right. \Leftrightarrow m = e_{}^2(tm)\]

Chọn: D

Câu 44.

Tập hợp các điểm biểu diễn của số phức z trên mặt phẳng tọa độ là đường tròn tâm I(0;1) bán kính R =3. Khi đó \[\left| {z – i} \right| = 3\]

Chọn: B

Câu 45.

Phương pháp:

Phương trình nhận được hai số phức z1 và z2 là nghiệm là \[\left( {z – z_1^{}} \right)\left( {z – z_2^{}} \right) = 0\]

Cách giải:

Cách giải:

Phương trình \[\left( {z – \sqrt 3 i} \right)\left( {z + \sqrt 3 i} \right) = 0 \Leftrightarrow \]\[z_{}^2 + 3 = 0\] nhận được hai số phức \[ – \sqrt 3 i\] và \[\sqrt 3 i\] là nghiệm

Chọn: B

Câu 46.

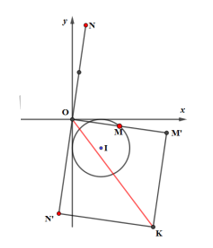
Phương pháp:

Sử dụng phương pháp hình học để tìm GTNN.

Cách giải:

Ta có \[\left| {z_1^{} – 1 + i} \right| = 1 \Leftrightarrow \]Điểm biểu diễn của z1 là

đường tròn (I(1;-1), R1 = 1)

Gọi M lần lượt là điểm biểu diễn của số phức z1, z2.

Giả sử

\[\begin{array}{l}z_1^{} = a + bi,z_2^{} = a’ + b’i(a,b,a’,b’ \in R)\\z_2^{} = 2iz_1^{} \Leftrightarrow a’ + b’i = 2( – b + ai)\end{array}\]

\[ \Rightarrow \]N là ảnh của M qua 2 phép biên hình: Phép quay tâm O một góc 900 và phép vị tự tâm O tỉ số 2

Gọi N’ là điểm đối xứng của N qua O. Dựng hình bình hành OM’KN’( như hình vẽ). Khi đó, điểm biểu diễn số phức 2z1-z2 là điểm K, \[P = \left| {2z_1^{} – z_2^{}} \right| = OK\].

Dễ dàng chứng minh được OM’KN’ là hình vuông, có cạnh OM’=2.OM\[ \Rightarrow OK = \sqrt 2 .OM’ = 2\sqrt 2 .OM\]

Nhận xét: OKmin khi và chỉ khi OMmin \[ \Leftrightarrow \]M là giao điểm của đoạn thẳng OI và đường tròn (I(1;-1),R1 =1)

Khi đó

 \[\begin{array}{l}OK = 2\sqrt 2 .OM\\ = 2\sqrt 2 (OI – R) = 2\sqrt 2 (\sqrt 2  – 1)\\ = 4 – 2\sqrt 2  \Rightarrow P_{\min }^{} = 4 – 2\sqrt 2 \end{array}\]

Chọn: D

Câu 47.

Phương pháp:

Gọi H, K lần lượt là hình chiếu của A lên (P) và D Khi đó, ta có:\[AH \le AK \Rightarrow \] Khoảng cách từ A đến Dnhỏ nhất bằng AH khi và chỉ khi K trùng H. Khi đó, D là đường thẳng đi qua M và H

Cách giải:

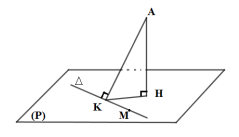
Gọi H, K lần lượt là hình chiếu của A lên (P) và D. Khi đó, ta có

\[AH \le AK \Rightarrow \] Khoảng cách từ A đến D nhỏ nhất bằng AH khi

và chỉ khi K trùng H.

Khi đó, D là đường thẳng đi qua M và H

Đường thẳng AH đi qua A và nhận  \[\overrightarrow {n_{(P)}^{}}  = (1;1;1)\] làm VTCP,

Có phương trình là \[\left\{ \begin{array}{l}x = 3 + t\\y = 2 + t\\z = 1 + t\end{array} \right.\]

Giả sử

 \[\begin{array}{l}H(3 + 1;2 + t;1 + t),H \in (P)\\ \Rightarrow 3 + t + 2 + t + 1 + t – 3 = 0\\ \Rightarrow t =  – 1\end{array}\]

\[ \Rightarrow H(2;1;0) \Rightarrow \overrightarrow {HM}  = (1; – 1;0)\]

\[ \Rightarrow \overrightarrow u  = (1; – 1;0) \Rightarrow P = a + b + c = 0\]

Chọn: D

Câu 48.

Phương pháp:

Sử dụng phương pháp hình học để tính giá trị của P

Chú ý: \[\left| {\frac{{z_1^{}}}{{z_2^{}}}} \right| = \frac{{\left| {z_1^{}} \right|}}{{\left| {z_2^{}} \right|}},a_{}^2 = b_{}^2 + c_{}^2 – 2bc\cos A\]

Cách giải:

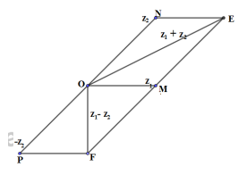
Ta có \[P = \left| {\frac{{z_1^{} + z_2^{}}}{{z_1^{} – z_2^{}}}} \right| = \frac{{\left| {z_1^{} + z_2^{}} \right|}}{{\left| {z_1^{} – z_2^{}} \right|}} = \frac{{OE}}{{OF}}\](quan sát hình vẽ)

\[\begin{array}{l}OE_{}^2 = OM_{}^2 + ME_{}^2 – 2.OM.ME.\cos 135_{}^0\\ = 2 + 4 – 2\sqrt 2 .2.\left( { – \frac{{\sqrt 2 }}{2}} \right) = 10\\ \Rightarrow OE = \sqrt {10} \\OF_{}^2 = OM_{}^2 + MF_{}^2 – 2.OM.MF.\cos 45_{}^0\\ = 2 + 4 – 2\sqrt 2 .2.\frac{{\sqrt 2 }}{2} = 2\\ \Rightarrow OE = \sqrt 2 \\ \Rightarrow P = \frac{{OE}}{{OF}} = \sqrt 5 \end{array}\]

Chọn: A

Câu 49.

Cách giải:

Gọi I là giao điểm của đường thẳng MN và mặt phẳng (P). Khi đó IE là tiếp tuyến của mặt cầu (S) đã cho và IM.IN=IE2

Ta có \[M(1;0;2),N(1; – 1; – 1) \Rightarrow \overrightarrow {MN}  = (0; – 1; – 3)\]

Phương trình đường thẳng MN là: \[\left\{ \begin{array}{l}x = 1\\y = t\\z = 2 + 3t\end{array} \right.\]

Giả sử

 \[\begin{array}{l}I(1;t;2 + 3t),I \in (P)\\ \Rightarrow 1 + 2t – 2 – 3t + 2 = 0\\ \Leftrightarrow t = 1 \Rightarrow I(1;1;5)\end{array}\]

\[\begin{array}{l} \Rightarrow IM = \sqrt {0 + 1 + 9}  = \sqrt {10} ,\\IN = \sqrt {0 + 4 + 36}  = 2\sqrt {10} ,\\IE_{}^2 = IM.IN = \sqrt {10} .2\sqrt {10}  = 20\\ \Rightarrow IE = 2\sqrt 5 \end{array}\]

Vậy, E luôn thuộc một đường tròn cố định có bán kính \[R = 2\sqrt 5 \]

Chọn: D

Câu 50

Phương pháp.

Nguyên hàm hai vế. Xác định hàm số f(x).

Từ đó khảo sát hàm số f(x), tìm điều kiện để f(x) = m có nghiệm duy nhất.

Cách giải:

Ta có \[f'(x) = (6x – 3x_{}^2)f(x)\],

\[\begin{array}{l}f(x) > 0,\forall x \in R\\ \Rightarrow \frac{{f'(x)}}{{f(x)}} = 6x – 3x_{}^2\\ \Rightarrow \int {\frac{{f'(x)}}{{f(x)}}dx = \int ( } 6x – 3x_{}^2)dx\end{array}\]

\[ \Leftrightarrow \ln (f(x)) = 3x_{}^2 – x_{}^3 + C \Leftrightarrow f(x) = e_{}^{3x_{}^2 – x_{}^3 + C}\]

Mà \[f(0) = 1 \Rightarrow e_{}^C = 1 \Rightarrow C = 0 \Rightarrow f(x) = e_{}^{3x_{}^2 – x_{}^3}\]

\[\begin{array}{l} \Rightarrow f'(x) = (6x – 3x_{}^2)e_{}^{3x_{}^2 – x_{}^3},\\f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\]

Bảng biến thiên:

 

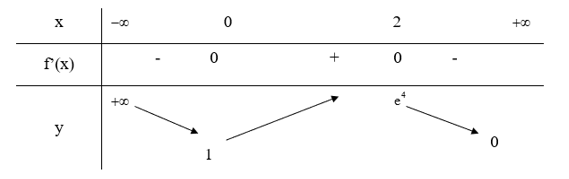
Để f(x) = m có nghiệm duy nhát thì \[\left[ \begin{array}{l}m > e_{}^4\\0 < m < 1\end{array} \right.\]

Chọn: A

 

Đề thi học kì 2 Toán lớp 12 có đáp án năm 2024 (15 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2023 – 2024

Môn: Toán lớp 12

Thời gian làm bài: 90 phút

(Đề 2)

Câu 1 (VD): Cho số phức \[z = x + yi\left( {x,y \in R} \right)\] có modun nhỏ nhất thỏa mãn điều kiện \[\left| {z – 4 – 2i} \right| = \left| {z – 2} \right|\]. Tính \[P = {x^2} + {y^2}\]

A. 32   

B. 16   

C. 8         

D. 10

Câu 2 (TH): Bất phương trình \[{\log _{\frac{1}{2}}}\left( {2x – 1} \right) \ge {\log _{\frac{1}{2}}}\left( {5 – x} \right)\] có tập nghiệm là

A. \[\left( {\frac{1}{2};2} \right]\]

B. \[\left[ {2; + \infty } \right)\]

C. \[\left[ {2;5} \right)\] 

D. \[\left( { – \infty ;2} \right]\]

Câu 3 (TH): Nếu modun của số phức z là r \[\left( {r > 0} \right)\] thì môdun của số phức \[\left( {1 – {i^3}} \right)z\] bằng

A. \[\sqrt 2 r\]   

B. 3r

C. 2r       

D. \[2\sqrt 2 r\]

Câu 4 (TH): Cho \[f\left( x \right) = {3^{\sqrt x }}\frac{{\ln 3}}{{\sqrt x }}\]. Hàm số nào dưới đây không phải là nguyên hàm của hàm số f(x)?

A. \[F\left( x \right) = {3^{\sqrt x }} + C\].      

B. \[F\left( x \right) = {2.3^{\sqrt x }} + C\].  

C. \[F\left( x \right) = 2\left( {{3^{\sqrt x }} – 1} \right) + C\].   

D. \[F\left( x \right) = 2\left( {{3^{\sqrt x }} + 1} \right) + C\].

Câu 5 (TH): Cho hình phẳng (H) giới hạn bởi đường parabol \[\left( P \right):y = {x^2} – x + 2\] và tiếp tuyến của đồ thị hàm số \[y = {x^2} + 1\] tại điểm có tọa độ (1;2). Diện tích của hình (H) là

A. \[\frac{5}{6}\]   

B. \[\frac{1}{6}\]

C. 1     

D. \[\frac{2}{3}\]

Câu 6 (TH): Tập nghiệm của bất phương trình \[{\left( {\sqrt {18}  + \sqrt {17} } \right)^{{x^2}}} < \frac{1}{{\sqrt {18}  – \sqrt {17} }}\] là

A. \[S = \left( { – 1;0} \right)\].   

B. \[S = \left[ { – 1;1} \right]\].

C. \[S = \left( {0;1} \right)\].     

D. \[S = \left( { – 1;1} \right)\].

Câu 7 (VD): Tìm giá trị của tham số m để hàm số \[y = {\log _3}\left[ {\left( {m – 1} \right){x^2} + 2mx + \left( {3m – 2} \right)} \right]\] có tập xác định là R.

A. \[\left( {1; + \infty } \right)\]   

B. \[\left( {2; + \infty } \right)\]

C. (1; 2)     

D. \[\left( { – \infty ;\frac{1}{2}} \right)\]

Câu 8 (TH): Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} + 4x – 2y + 6{\rm{z}} – 11 = 0\] và mặt phẳng \[\left( P \right):x – 2y + 2z + 1 = 0\]. Gọi ( C) là đường tròn giao tuyến của (P) và (S). Tính chu vi đường tròn (C).

A. \[6\pi \] 

B. \[8\pi \]

C. \[10\pi \]   

D. \[4\pi \]

Câu 9 (VD): Một nhóm từ thiện ở Hà Nội khởi công dự án xây cầu bằng bê tông như hình vẽ (đường cong trong hình là các đường parablol). Thể tích khối bê tông đủ để đổ cho cây cầu gần nhất với kết quả nào sau đây?

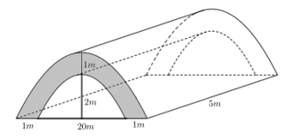
A. 84m3                         B. 88m3

C. 85m3                         D. 90m3

Câu 10 (TH): Trong không gian Oxyz, đường thẳng \[\left( d \right):\frac{{x – 2}}{3} = \frac{{y + 1}}{{ – 2}} = \frac{{z – 4}}{4}\] có phương trình tham số là

A. \[\left\{ {\begin{array}{*{20}{l}}{x =  – 2 + 3t}\\{y = 1 – 2t}\\{z =  – 4 + 4t}\end{array}} \right.,{\mkern 1mu} {\mkern 1mu} t \in R\]    

B. \[\left\{ {\begin{array}{*{20}{l}}{x = 2 – 3m}\\{y =  – 1 + 2m}\\{z = 4 – 4m}\end{array}} \right.,{\mkern 1mu} {\mkern 1mu} m \in R\]

C. \[\left\{ {\begin{array}{*{20}{l}}{x =  – 2 + 3\tan t}\\{y = 1 – 2\tan t}\\{z =  – 4 + 4\tan t}\end{array}} \right.,{\mkern 1mu} {\mkern 1mu} t \in R\]

D. \[\left\{ {\begin{array}{*{20}{l}}{x = 2 – 3\cos t}\\{y =  – 1 + 2\cos t}\\{z =  – 4 – 4\cos t}\end{array}} \right.,{\mkern 1mu} {\mkern 1mu} t \in R\]

Câu 11 (TH): Hàm số \[F\left( x \right)\] nào sau đây là một nguyên hàm của hàm số \[f\left( x \right) = \frac{{x + 3}}{{{x^2} + 4x + 3}}\]?

A. \[F\left( x \right) = 2\ln \left| {x + 3} \right| – \ln \left| {x + 1} \right| + C\]

B. \[F\left( x \right) = \ln \left( {2\left| {x + 1} \right|} \right)\]

C. \[F\left( x \right) = \ln \left| {\frac{{x + 1}}{{x + 3}}} \right| + 2\]

D.  \[F\left( x \right) = \ln \left[ {\left( {x + 1} \right)\left( {x + 3} \right)} \right]\]

Câu 12 (VD): Trong không gian Oxyz, cho hai đường thẳng \[\left( d \right):\frac{{x – 3}}{{ – 2}} = \frac{{y – 6}}{2} = \frac{{z – 1}}{1}\], \[\left( {d’} \right):x = t;y =  – t;z = 2\]. Đường thẳng đi qua A(0;1; 1) cắt (d’) và vuông góc với (d) có phương trình là

A. \[\frac{{x – 1}}{{ – 1}} = \frac{y}{{ – 3}} = \frac{{z – 1}}{4}\].   

B. \[\frac{x}{{ – 1}} = \frac{{y – 1}}{3} = \frac{{z – 1}}{4}\].

C. \[\frac{x}{{ – 1}} = \frac{{y – 1}}{{ – 3}} = \frac{{z – 1}}{4}\].   

D. \[\frac{x}{1} = \frac{y}{{ – 3}} = \frac{{z – 1}}{4}\].

Câu 13 (TH): Cho số phức \[z{\rm{ }} = 2 + 3i\], khi đó \[\frac{z}{{\bar z}}\] bằng

A. \[\frac{{5 – 12i}}{{13}}\] 

B. \[\frac{{ – 5 – 12i}}{{13}}\]

C. \[\frac{{ – 5 + 12i}}{{13}}\]   

D. \[\frac{{5 – 6i}}{{11}}\]

Câu 14 (TH): Cho số phức \[z = a + \left( {a – 5} \right)i\]. Tìm a để điểm biểu diễn của số phức nằm trên đường phân giác của góc phần tư thứ hai và thứ tư.

A. \[a =  – \frac{1}{2}\] 

B. \[a = \frac{5}{2}\]

C.a= 0       

D. \[a = \frac{3}{2}\]

Câu 15 (TH): Trong không gian Oxyz, phương trình mặt cầu (S) đường kính AB với \[A\left( {4; – 3;5} \right),B\left( {2;1;3} \right)\] là

A. \[{x^2} + {y^2} + {z^2} + 6x + 2y – 8z – 26 = 0\]

B. \[{x^2} + {y^2} + {z^2} – 6x + 2y – 8z + 20 = 0\]

C. \[{x^2} + {y^2} + {z^2} + 6x – 2y + 8z – 20 = 0\]

D. \[{x^2} + {y^2} + {z^2} – 6x + 2y – 8z + 26 = 0\]

Câu 16 (TH): Trong không gian Oxyz, cho hai véc tơ \[\vec u = \vec i\sqrt 3  + \vec k,\vec v = \vec j\sqrt 3  + \vec k\]. Khi đó tích vô hướng của \[\vec u.\vec v\] bằng

A. 2             

B. 1

C. −3 

D. 3

Câu 17 (TH): Gọi S là tập hợp tất cả các số nguyên dương của tham số m sao cho bất phương trình \[{4^x} – m{.2^x} – m + 15 \ge 0\] có nghiệm đúng với mọi \[x \in \left[ {1;2} \right]\]. Tính số phần tử của S.

A. 7       

B. 4

C. 9   

D. 6

Câu 18 (TH): Trong không gian Oxyz, cho hai đường thẳng \[\left( {{d_1}} \right):\frac{{x – 7}}{1} = \frac{{y – 3}}{2} = \frac{{z – 9}}{{ – 1}}\] và \[\left( {{d_2}} \right):\frac{{x – 3}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 1}}{3}\]. Chọn khẳng định đúng trong các khẳng định sau:

A. (d1) và (d2) cắt nhau.

B. (d1) và (d2) vuông góc với nhau. 

C. (d1) và (d2) trùng nhau.   

D. (d1) và (d2) chéo nhau.

Câu 19 (VD): Tìm các giá trị của tham số m để bất phương trình \[{\log _2}\left( {2{x^2} – 5x + 1} \right) – m > m\sqrt {{{\log }_4}\left( {2{x^2} – 5x + 1} \right)} \] có nghiệm đúng với mọi \[x \ge 3\].

A.m< 1     

B. \[m \ge 1\]

C.m> 1     

D. \[m \le 1\]

Câu 20 (TH): Trong hệ tọa độ Oxy, cho điểm M biểu diễn số phức \[z =  – 2 + 3i\] . Gọi N là điểm thuộc đường thẳng y=3 sao cho tam giác OMN cân tại O. Điểm N là điểm biểu diễn của số phức nào dưới đây?

A. \[z = 3 – 2i\]     

B. \[z = \; – 2 – 3i\]

C. \[z = 2 + 3i\] 

D. \[z = \; – 2 + i\]

Câu 21 (TH): Giả sử \[{z_1},{z_2}\] là hai nghiệm của phương trình \[{z^2} – 2z + 5 = 0\]. Gọi M, N lần lượt là các điểm biểu diễn của \[{z_1},{z_2}\] trên hệ tọa độ Oxy. Tọa độ trung điểm của đoạn thẳng MN là:

A.(1; 0)       

B. (1; 1)

C.(0; 0)     

D. (0;1)

Câu 22 (VD): Cho số phức z thỏa mãn \[\frac{{{{\left| z \right|}^2}}}{z} – \frac{{z – i}}{{1 – i}} = 3i\]. Trên hệ tọa độ Oxy, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z là

A. 3           

B. 4

C. −5       

D. 5

Câu 23 (TH): Trong không gian Oxyz, cho ba điểm \[A\left( {2;1; – 1} \right),B\left( {0; – 1;3} \right),C\left( {1;2;1} \right)\]. Mặt phẳng (P) qua B và vuông góc với AC có phương trình là:

A. \[x + y + 2z + 5 = 0\]     

B. \[x – y – 2z + 5 = 0\]        

C. \[x – y + 2z + 5 = 0\]  

D. \[x + y – 2z + 5 = 0\]

Câu 24 (TH): Trong không gian Oxyz, cho các điểm \[A\left( {0;{\mkern 1mu}  – 2;{\mkern 1mu}  – 1} \right),B\left( {1;{\mkern 1mu}  – 1;{\mkern 1mu} 2} \right)\]. Tìm điểm M trên đoạn thẳng AB sao cho MA = 2MB.

A. \[\left( {\frac{1}{2};{\mkern 1mu} \frac{{ – 3}}{2};{\mkern 1mu} \frac{1}{2}} \right)\]    B.(2; 0; 5)

C. \[\left( {\frac{2}{3};{\mkern 1mu} \frac{{ – 4}}{3};{\mkern 1mu} 1} \right)\]  D. \[\left( { – 1;{\mkern 1mu}  – 3;{\mkern 1mu}  – 4} \right)\].

Câu 25 (TH): Trên hệ tọa độ Oxy, gọi M là điểm biểu diễn của số phức z có mô đun lớn nhất thỏa mãn: \[\left| {z + 4 – 3i} \right| = 5\]. Tọa độ của điểm M là

A. (-6; 8)               B.(8; -6)                    

C.(8; 6)                 D. (- 8; 6)

Câu 26 (NB): Cho hai hàm số y = f(x); y = g(x) liên tục trên \[\left[ {a;{\mkern 1mu} b} \right]{\mkern 1mu} \left( {a < b} \right)\] và có đồ thị lần lượt là \[\left( {{C_1}} \right),\left( {{C_2}} \right)\]. Khi đó, công thức tính diện tích hình phẳng giới hạn bởi \[\left( {{C_1}} \right),\left( {{C_2}} \right)\] và hai đường thẳng x = a; x = b là

A. \[\left| {\int\limits_a^b {\left( {f\left( x \right) – g\left( x \right)} \right){\rm{d}}x} } \right|\]

B. \[\int\limits_a^b {\left[ {f\left( x \right) – g\left( x \right)} \right]{\rm{d}}x} \]

C. \[\int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|{\rm{d}}x} \]    

D. \[\int\limits_a^b {f\left( x \right){\rm{d}}x}  + \int\limits_a^b {g\left( x \right){\rm{d}}x} \]

Câu 27 (TH): Trong không gian Oxyz, phương trình mặt cầu (S) tiếp xúc với hai mặt phẳng song song \[\left( P \right):x – 2y + 2z + 6 = 0\] và \[\left( Q \right):x – 2y + 2z – 10 = 0\] có tâm I ở trên trục Oy là:

A. \[{x^2} + {y^2} + {z^2} + 2y – \frac{{55}}{9} = 0\]

B. \[{x^2} + {y^2} + {z^2} – 2y – \frac{{55}}{9} = 0\]

C. \[{x^2} + {y^2} + {z^2} + 2y – 60 = 0\]

D. \[{x^2} + {y^2} + {z^2} – 2y + 55 = 0\]

Câu 28 (TH): Cho hình phẳng (H) như hình vẽ (phần tô đậm). Diện tích hình phẳng (H) là

A. \[\frac{9}{2}\ln 3 – \frac{3}{2}\] 

B. 1.

C. \[\frac{9}{2}\ln 3 – 4\].

D. \[\frac{9}{2}\ln 3 – 2\].

Câu 29 (VD): Trong không gian Oxyz, cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} + 2x – 2y + 6z – 5 = 0\] và mặt phẳng \[\left( P \right):x – 2y + 2z + 3 = 0\]. Gọi M là tiếp điểm của (S) và mặt phẳng (Q) di động vuông góc với mặt phẳng (P). Tập hợp các điểm M là

    A. Đường tròn: \[{x^2} + {y^2} + {z^2} + 2x – 2y + 6z – 5 = 0;x – 2y + 2z + 9 = 0\]

    B. Mặt phẳng: \[x – 2y + 2z – 9 = 0\]

    C. Đường tròn: \[{x^2} + {y^2} + {z^2} + 2x – 2y + 6z – 5 = 0;x – 2y + 2z – 9 = {\rm{ }}0\]

    D. Mặt phẳng: \[x – 2y + 2z + 9 = 0\]

Câu 30 (TH): Tổng phần thực phần ảo của số phức z = 3- i là

A. 2.           

B. −1.  

C. −2.         

D. 3.

Câu 31 (TH): Cho \[0 < a < \frac{\pi }{2}\] và \[\int\limits_0^a {x\tan x{\rm{d}}x}  = m\]. Tính \[I = \int\limits_0^a {{{\left( {\frac{x}{{\cos x}}} \right)}^2}{\rm{d}}x} \] theo a và m.

A. \[I = {a^2}\tan a – 2m\]     

B. \[I =  – {a^2}\tan a + m\] 

C. \[I = a\tan a – 2m\]   

D. \[I = {a^2}\tan a – m\]

Câu 32 (TH): Tìm số phức liên hợp của số phức \[z = i\left( {3i – 1} \right)\].

A. \[\bar z = 3 – i\].

B. \[\bar z =  – 3 + i\].

C. \[\bar z = 3 + i\].   

D. \[\bar z =  – 3 – i\].

Câu 33 (TH): Biết \[\int\limits_0^\pi  {x\sin x{\rm{d}}x}  = a\pi  + b\left( {a,b \in R} \right)\]. Tổng a+ b là

A. 3           

B. 2

C. −3       

D. 1

Câu 34 (TH): Trong không gian Oxyz, tìm điều kiện của tham số m để phương trình \[{x^2} + {y^2} + {z^2} – 2mx + 4y + 2mz + {m^2} + 5m = 0\] là phương trình mặt cầu.

A.m<  4.       

B. \[\left[ {\begin{array}{*{20}{l}}{m \le 1}\\{m \ge 4}\end{array}} \right.\]

C. m> 1       

D. \[\left[ {\begin{array}{*{20}{l}}{m < 1}\\{m > 4}\end{array}} \right.\]

Câu 35 (TH): Số nào trong các số sau là số thuần ảo?

A. \[\left( {\sqrt 3  + 2i} \right)\left( {\sqrt 3  – 2i} \right)\]   

B. \[\left( {\sqrt 3  + 2i} \right) + \left( {\sqrt 3  – 2i} \right)\]

C. \[\frac{{1 – 4i}}{{1 + 4i}}\] 

D. \[{\left( {3 + 3i} \right)^2}\]

Câu 36 (VD): Cho số phức z thỏa mãn điều kiện \[\left| {z – 1 + 2i} \right| \le 2\]. Trong hệ tọa độ Oxy, tập hợp điểm biểu diễn số phức \[w = 3z – 2 + i\], là hình tròn có diện tích bằng

A. \[25\pi \].                   B. \[16\pi \].  

C. \[36\pi \].                   D. \[9\pi \].

Câu 37 (TH): Tích phân \[\int\limits_0^1 {x\sqrt {{x^2} + 1} {\mkern 1mu} {\rm{d}}x} \] bằng

A. \[\frac{{2\sqrt 2  – 1}}{3}\]       

B. \[2\sqrt 2  + \frac{{15}}{{16}}\]

C. \[2\sqrt 2  + \frac{9}{{10}}\]   

D. \[\frac{{2\sqrt 2  + 1}}{3}\]

Câu 38 (VD): Cho số phức \[z = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + … + {\left( {1 + i} \right)^{2018}}\]. Mệnh đề nào sau đây đúng

A. \[z =  – {2^{1009}}\]

 B. \[z =  – {2^{1009}} + \left( {{2^{1009}} + 1} \right)i\]

C. \[z = {2^{1009}} + \left( {{2^{1009}} + 1} \right)i\]

D. \[z = {2^{1009}} + {2^{1009}}i\]

Câu 39 (VD): Cho hàm số \[y = {\rm{lo}}{{\rm{g}}_a}x\] và \[y = {\rm{lo}}{{\rm{g}}_b}x\] có đồ thị lần lượt là (C) và (C′) (như hình vẽ bên). Đường thẳng x = 9 cắt trục hoành và các đồ thị (C) và (C′) lần lượt tại M, N, P. Biết rằng MN  = NP, hãy xác định biểu thức liên hệ giữa a và b.

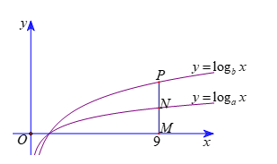
A. \[a = {b^2}\]              B. a = 9b

C. a = 3b                        D. a= b + 3

Câu 40 (VD): Cho hình phẳng (H) giới hạn bởi các đường \[y = \sqrt {\ln x} ,y = 0,x = 1\] và \[x = k{\mkern 1mu} \left( {k > 1} \right)\]. Kí hiệu \[{V_k}\] là thể tích khối tròn xoay thu được khi quay hình (H) quanh trục Ox. Biết rằng \[{V_k} = \pi \]. Hãy chọn mệnh đề đúng trong các mệnh đề sau:

A. 4< k< 5.                    B.1< k< 2.

C.2< k< 3.                     D.3<k< 4.

Câu 41 (VD): Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm \[M\left( {2; – 4;1} \right)\] và chắn trên các trục tọa độ Ox, Oy,Oz theo ba đoạn có độ dài lần lượt là a; b; c. Phương trình tổng quát của mặt phẳng (P) khi a; b; c theo thứ tự tạo thành một cấp số nhân có công bội bằng 2 là:

A. \[4x + 2y – z – 1 = 0\]

B. \[4x – 2y + z + 1 = 0\]                              

C. \[16x + 4y – 4z – 1 = 0\]     

D. \[4x + 2y + z – 1 = 0\]

Câu 42 (TH): Trong không gian Oxyz, cho hình bình hành ABCD với \[A\left( {1;1;0} \right),B\left( {1;1;2} \right),D\left( {1;0;2} \right)\]. Diện tích hình bình hành ABCD bằng:

A. 4                               B. 3

C. 1                               D. 2

Câu 43 (NB): Cho hàm số f(x) có đạo hàm f’(x) liên tục liên tục trên đoạn [a; b]. Biết f(a) = 5 và \[\int\limits_a^b {f’\left( x \right)dx}  = 2\sqrt 5 \], tính f(b).

A. \[\sqrt 5 \left( {2 – \sqrt 5 } \right)\] 

B. \[\sqrt 5 \left( {\sqrt 5  + 2} \right)\]

C. \[\sqrt 2 \left( {\sqrt 5  – 2} \right)\]   

D. \[\sqrt 5 \left( {\sqrt 5  – 2} \right)\]

Câu 44 (VD): Cho \[\int\limits_0^6 {f\left( x \right)dx}  = 1.\] Tình \[\int\limits_0^2 {f\left( {3x} \right)dx} \].

A. I = -3            B. I = 1 

C.I = 3               D. \[I = \frac{1}{3}\]

Câu 45 (TH): Cho hai số phức \[z = 3 + 2i\] và \[w = 3 – 2i\]. Khẳng định nào sau đây là khẳng định sai?

    A. \[\left| z \right| > \left| w \right|\]

    B. \[\left| z \right| = \left| w \right|\]

    C. Nếu A và B theo thứ tự là hai điểm biểu diễn của z và w trên hệ tọa độ Oxy thì \[AB = \left| {z – w} \right|\].

    D. Số phức z là số phức liên hợp của số phức w.

Câu 46 (VD): Cho \[I = \int\limits_0^2 {\left( {2{x^2} – x – m} \right){\rm{d}}x} \] và \[J = \int\limits_0^1 {\left( {{x^2} – 2mx} \right){\rm{d}}x} \]. Tìm điều kiện của tham số m để \[I \ge J\].

A. \[m \ge \frac{{11}}{3}\].   

B. \[m \ge 3\].  

C. \[m \le \frac{{11}}{3}\].   

D. \[m \le 3\].

Câu 47 (TH): Tập nghiệm của bất phương trình \[{3^{2x + 1}} > {\left( {\frac{1}{3}} \right)^{ – 3{x^2}}}\] là:

A. \[\left( { – \infty ; – \frac{1}{3}} \right) \cup \left( {1; + \infty } \right)\]

B. \[\left( {1; + \infty } \right)\]             

C. \[\left( { – \infty ; – \frac{1}{3}} \right)\]

D. \[\left( { – \frac{1}{3};1} \right)\]

Câu 48 (VD): Trong không gian Oxyz, cho tứ diện ABCD có \[A\left( {3; – 2;1} \right),B\left( { – 4;0;3} \right),C\left( {1;4; – 3} \right),D\left( {2;3;5} \right)\]. Phương trình mặt phẳng chứa AC và song song với BD là:

A. \[12x – 10y – 21z – 35 = 0\]

B. \[12x + 10y – 21z + 35 = 0\]

C. \[12x + 10y + 21z + 35 = 0\]

D. \[12x – 10y + 21z – 35 = 0\]

Câu 49 (TH): Bất phương trình \[\log _2^2x – {\log _2}\left( {4x} \right) < 0\] có số nghiệm nguyên là:

A. 3                               B. 2

C. 1                               D. 0

Câu 50 (VD): Trong không gian Oxyz, gọi (P) là mặt phẳng đi qua H(3; 1; 0)= và cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho H là trực tâm của tam giác ABC. Khoảng cách từ điểm \[M\left( {1;1;0} \right)\] đến mặt phẳng (P) là:

A. \[\frac{2}{{\sqrt {10} }}\]   

B. \[\frac{6}{{\sqrt {10} }}\]

C. \[\frac{3}{{\sqrt {10} }}\]   

D. \[\frac{5}{{\sqrt {10} }}\]

 

Đáp án

1-C	2-A	3-A	4-A	5-B	6-D	7-B	8-B	9-B	10-C
11-B	12-D	13-C	14-B	15-B	16-B	17-D	18-D	19-A	20-C
21-A	22-D	23-B	24-C	25-D	26-C	27-B	28-D	29-A	30-A
31-A	32-B	33-D	34-D	35-D	36-C	37-A	38-C	39-A	40-C
41-D	42-D	43-B	44-D	45-A	46-D	47-D	48-A	49-A	50-B

 

LỜI GIẢI CHI TIẾT

Câu 1: Đáp án C

Ta có: \[\left| {x + yi – 4 – 2i} \right| = \left| {x + yi – 2} \right|\]\[ \Leftrightarrow \left| {\left( {x – 4} \right) + \left( {y – 2} \right)i} \right| = \left| {\left( {x – 2} \right) + yi} \right|\]

\[ \Leftrightarrow \sqrt {{{\left( {x – 4} \right)}^2} + {{\left( {y – 2} \right)}^2}}  = \sqrt {{{\left( {x – 2} \right)}^2} + {y^2}} \]

\[ \Leftrightarrow {\left( {x – 4} \right)^2} + {\left( {y – 2} \right)^2} = {\left( {x – 2} \right)^2} + {y^2}\]

\[ \Leftrightarrow {x^2} – 8x + 16 + {y^2} – 4y + 4 = {x^2} – 4x + 4 + {y^2}\]

\[ \Leftrightarrow x + y – 4 = 0 \Leftrightarrow y = 4 – x\]

\[\left| z \right| = \sqrt {{x^2} + {y^2}}  = \sqrt {{x^2} + {{\left( {4 – x} \right)}^2}}  = \sqrt {2{{\left( {x – 2} \right)}^2} + 8}  \ge \sqrt 8  = 2\sqrt 2 \]

Vậy môdun nhỏ nhất của số phức z bằng \[2\sqrt 2 \]

Suy ra \[P = {x^2} + {y^2} = 8\].

Câu 2: Đáp án A

ĐK: \[\left\{ {\begin{array}{*{20}{l}}{2x – 1 > 0}\\{5 – x > 0}\end{array}} \right. \Leftrightarrow \frac{1}{2} < x < 5\]

Ta có \[{\log _{\frac{1}{2}}}\left( {2x – 1} \right) \ge {\log _{\frac{1}{2}}}\left( {5 – x} \right) \Leftrightarrow 2x – 1 \le 5 – x \Leftrightarrow x \le 2\] kết hợp điều kiện ta có nghiệm của bất phương trình \[\frac{1}{2} < x \le 2\].

Câu 3: Đáp án A

Ta có: \[\left( {1 – {i^3}} \right)z = \left( {1 + i} \right)z\]

\[ \Rightarrow \left| {\left( {1 – {i^3}} \right)z} \right| = \left| {\left( {1 + i} \right)z} \right| = \left| {1 + i} \right|.\left| z \right| = \sqrt 2 r\]

Câu 4: Đáp án A

Đặt \[\sqrt x  = t\left( {t > 0} \right) \Leftrightarrow \frac{1}{{2\sqrt x }}dx = dt \Leftrightarrow dx = 2t.dt\], khi đó

\[F\left( x \right) = \mathop \smallint \nolimits^ f\left( x \right)dx = \mathop \smallint \nolimits^ {3^{\sqrt x }}.\frac{{\ln 3}}{{\sqrt x }}{\rm{d}}x\].

\[\begin{array}{l} = \ln 3\mathop \smallint \nolimits^ {3^t}.\frac{1}{t}2tdt\\ = 2\ln 3\mathop \smallint \nolimits^ {3^t}dt\\ = 2\ln 3.\frac{{{3^t}}}{{\ln 3}} + {C_1} = \\{2.3^t} + {C_1} = {2.3^{\sqrt x }} + {C_1}\end{array}\]

Vì ta được chọn hằng số \[{C_1}\]  nên với \[{C_1} = C – 2\] thì \[F\left( x \right) = 2\left( {{3^{\sqrt x }} – 1} \right) + C\]

Với \[{C_1} = C + 2\] thì \[F\left( x \right) = 2\left( {{3^{\sqrt x }} + 1} \right) + C\]

Từ đó ta có B, C, D đúng, A sai.

Câu 5: Đáp án B

Đặt \[y = f\left( x \right) = {x^2} + 1\], ta có: \[f’\left( x \right) = 2x\].

Phương trình tiếp tuyến d của parabol \[y = {x^2} + 1\] tại điểm có tọa độ (1; 2) có dạng

\[y = f’\left( 1 \right)\left( {x – 1} \right) + 2 = 2\left( {x – 1} \right) + 2\] hay y= 2x

Phương trình hoành độ giao điểm của d và (P):

\[{x^2} – x + 2 = 2x \Leftrightarrow {x^2} – 3x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 2}\end{array}} \right.\]

Diện tích của hình (H) là: \[S\left( x \right) = \mathop \smallint \limits_1^2 \left| {{x^2} – 3x + 2} \right|{\rm{d}}x = \frac{1}{6}\]

Câu 6: Đáp án D

Ta có

 \[\begin{array}{l}{\left( {\sqrt {18}  + \sqrt {17} } \right)^{{x^2}}} < \frac{1}{{\sqrt {18}  – \sqrt {17} }}\\ \Leftrightarrow {\left( {\sqrt {18}  + \sqrt {17} } \right)^{{x^2}}} < \sqrt {18}  + \sqrt {17} \\ \Leftrightarrow {x^2} < 1 \Leftrightarrow  – 1 < x < 1\end{array}\]

Vậy tập nghiệm bất phương trình S = (-1; 1).

Câu 7: Đáp án B

Hàm số có tập xác định là \[\mathbb{R} \Leftrightarrow \left( {m – 1} \right){x^2} + 2mx + \left( {3m – 2} \right) > 0,\forall x \in \mathbb{R}\,\,\left( 1 \right)\]

Với  m = 1  (1) trở thành \[2x + 1 > 0,\forall x \in \mathbb{R}\] (vô lý) ⇒ loại m = 1.

Với \[m \ne 1\],

 \[\begin{array}{l}\left( 1 \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta ‘ < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m – 1 > 0}\\{{m^2} – \left( {m – 1} \right)\left( {3m – 2} \right) < 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > 1}\\{ – 2{m^2} + 5m – 2 < 0}\end{array}} \right. \Leftrightarrow m > 2\end{array}\].

Vậy \[m \in \left( {2; + \infty } \right)\]

Câu 8: Đáp án B

Mặt cầu (S) có tâm \[I\left( { – 2;1; – 3} \right)\] và bán kính \[R = \sqrt {{{\left( { – 2} \right)}^2} + {1^2} + {{\left( { – 3} \right)}^2} + 11}  = \sqrt {25}  = 5\].

Khoảng cách từ tâm I đến mặt phẳng (P) là:

   \[d = d\left( {I;\left( P \right)} \right) = \frac{{\left| { – 2 – 2.1 + 2.\left( { – 3} \right) + 1} \right|}}{{\sqrt {1 + {{\left( { – 2} \right)}^2} + {2^2}} }} = \frac{9}{3} = 3\]

=> Bán kính đường tròn giao tuyến là \[r = \sqrt {{R^2} – {d^2}}  = \sqrt {{5^2} – {3^2}}  = \sqrt {16}  = 4\].

Chu vi đường tròn giao tuyến (C) là: \[2\pi r = 8\pi \].

Câu 9: Đáp án B

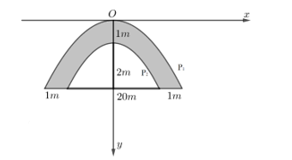
Thiết diện của cây cầu cắt bởi mặt phẳng vuông góc với chiều dài có dạng như hình dưới.

Chọn hệ trục Oxy như hình vẽ.

\[\left( {{P_1}} \right):y = {a_1}{x^2},\left( {{P_2}} \right):y = {a_2}{x^2} + 1\]

Điểm \[A\left( {11;3} \right) \in \left( {{P_1}} \right) \Rightarrow {a_1} = \frac{3}{{121}} \Rightarrow \left( {{P_1}} \right):y = \frac{3}{{121}}{x^2}\].

Điểm \[B\left( {10;3} \right) \in \left( {{P_1}} \right) \Rightarrow {a_2} = \frac{1}{{50}} \Rightarrow \left( {{P_2}} \right):y = \frac{1}{{50}}{x^2} + 1\].  

Diện tích hình phẳng giới hạn bởi \[\left( {{P_1}} \right)\] và đường thẳng y= 3 là:

 \[{S_1} = \mathop \smallint \limits_{ – 11}^{11} \left( {3 – \frac{3}{{121}}{x^2}} \right){\rm{d}}x = 44\]

Diện tích hình phẳng giới hạn bởi (P2) và đường thẳng y= 3 là:

  \[{S_2} = \mathop \smallint \limits_{ – 10}^{10} \left[ {3 – \left( {\frac{1}{{50}}{x^2} + 1} \right)} \right]{\rm{d}}x = \frac{{80}}{3}\]

Diện tích thiết diện của cây cầu cắt bởi mặt phẳng vuông góc với chiều dài của cây cầu là: \[S = {S_1} – {S_2} = \frac{{52}}{3}\left( {{{\rm{m}}^2}} \right)\]

Thể tích bê tông cần dùng là: \[V = S.l = \frac{{52}}{3}.5 = \frac{{260}}{3} \approx 86,67\left( {{{\rm{m}}^3}} \right)\]

Câu 10: Đáp án C

Ta có \[\left( d \right):\frac{{x – 2}}{3} = \frac{{y + 1}}{{ – 2}} = \frac{{z – 4}}{4}\] nên d có VTCP là \[\vec u = \left( { – 3;2; – 4} \right)\] và đi qua điểm \[M\left( {2; – 1;4} \right)\] nên có phương trình tham số \[\left\{ {\begin{array}{*{20}{l}}{x = 2 – 3t}\\{y =  – 1 + 2t}\\{z = 4 – 4t}\end{array}} \right.,{\mkern 1mu} {\mkern 1mu} t \in R\]

Câu 11: Đáp án B

\[\begin{array}{l}\mathop \smallint \nolimits^ f\left( x \right){\rm{d}}x = \mathop \smallint \nolimits^ \frac{{x + 3}}{{{x^2} + 4x + 3}}{\rm{d}}x\\ = \mathop \smallint \nolimits^ \frac{1}{{x + 1}}{\rm{d}}x = \ln \left| {x + 1} \right| + C\end{array}\]

Câu 12: Đáp án D

Đường thẳng \[\left( d \right):\frac{{x – 3}}{{ – 2}} = \frac{{y – 6}}{2} = \frac{{z – 1}}{1}\] có VTCP \[\overrightarrow {{u_{\left( d \right)}}}  = \left( { – 2;2;1} \right)\]

Gọi phương trình cần tìm là \[\left( {\rm{\Delta }} \right)\]

Gọi M là giao điểm của (Δ) và (d′). Suy ra \[M\left( {t; – t;2} \right)\]

Ta có: \[\overrightarrow {AM}  = \left( {t; – t – 1;1} \right),\overrightarrow {{u_{\left( d \right)}}}  = \left( { – 2;2;1} \right)\].

Lại có: \[\overrightarrow {AM} .\overrightarrow {{u_{\left( d \right)}}}  = 0\]

\[\begin{array}{l} \Leftrightarrow  – 2t – 2\left( {t + 1} \right) + 1 = 0\\ \Leftrightarrow  – 4t = 1 \Leftrightarrow t =  – \frac{1}{4}\end{array}\]

Do đó \[\overrightarrow {AM}  = \left( { – \frac{1}{4}; – \frac{3}{4};1} \right)\].

\[\left( {\rm{\Delta }} \right)\] qua A(0; 1; 1) và nhận vectơ \[\vec u = 4\overrightarrow {AM}  = \left( { – 1; – 3;4} \right)\] có phương trình là:

\[\frac{x}{{ – 1}} = \frac{{y – 1}}{{ – 3}} = \frac{{z – 1}}{4}\].

Câu 13: Đáp án C

\[\frac{z}{{\bar z}} = \frac{{2 + 3i}}{{2 – 3i}} = \frac{{{{\left( {2 + 3i} \right)}^2}}}{{{2^2} – {3^2}{i^2}}} = \frac{{ – 5 + 12i}}{{13}}\].

Câu 14: Đáp án B

Đường phân giác của góc phần tư thứ hai và thứ tư là d: y= -x.

Gọi \[M\left( {a;a – 5} \right)\] là điểm biểu diễn của z.

Ta có: \[M \in \left( d \right) \Leftrightarrow a – 5 =  – a \Leftrightarrow a = \frac{5}{2}\].

Câu 15: Đáp án B

\[AB = \sqrt {{2^2} + {{\left( { – 4} \right)}^2} + {2^2}}  = 2\sqrt 6 \] suy ra bán kính \[R = \sqrt 6 \].

Trung điểm của AB là I(3; -1; 4).

Vậy phương trình mặt cầu là

\[\begin{array}{l}\left( S \right):{\left( {x – 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {x – 4} \right)^2} = 6\\ \Leftrightarrow {x^2} + {y^2} + {z^2} – 6x + 2y – 8z + 20 = 0\end{array}\]

Câu 16: Đáp án B

Ta có \[\vec u = \vec i\sqrt 3  + \vec k \Rightarrow \vec u = \left( {\sqrt 3 ;0;1} \right)\] và \[\vec v = \vec j\sqrt 3  + \vec k \Rightarrow \vec v = \left( {0;\sqrt 3 ;1} \right)\]

Suy ra \[\vec u.\vec v = \sqrt 3 .0 + 0.\sqrt 3  + 1.1 = 1\]

Câu 17: Đáp án D

\[{4^x} – m{.2^x} – m + 15 \ge 0\quad \left( 1 \right)\]

Đặt \[{2^x} = t\left( {t > 0} \right)\] ta được \[{t^2} – mt – m + 15 \ge 0\quad \left( 2 \right)\]

Để bất phương trình (1) đúng với mọi \[x \in \left[ {1;2} \right]\] thì (2) đúng với mọi \[t \in \left[ {2;4} \right]\].

Ta có \[\left( 2 \right) \Leftrightarrow {t^2} + 15 \ge m\left( {t + 1} \right) \Leftrightarrow \frac{{{t^2} + 15}}{{t + 1}} \ge m\].

Xét hàm số \[f\left( t \right) = \frac{{{t^2} + 15}}{{t + 1}},{\mkern 1mu} t \in \left[ {2;4} \right]\]. Ta có \[f’\left( t \right) = \frac{{\left( {t + 5} \right)\left( {t – 3} \right)}}{{{{\left( {t + 1} \right)}^2}}};f’\left( t \right) = 0 \Leftrightarrow t = 3\]

BBT

 

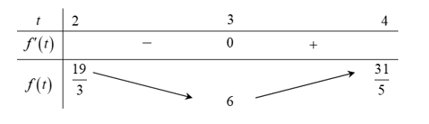
Vậy suy ra \[m \le 6\]

Câu 18: Đáp án D

Đường thẳng \[\left( {{d_1}} \right):\frac{{x – 7}}{1} = \frac{{y – 3}}{2} = \frac{{z – 9}}{{ – 1}}\] có VTCP \[\overrightarrow {{u_1}}  = \left( {1;2; – 1} \right)\] và đi qua điểm \[{M_1}\left( {7;3;9} \right)\]

Đường thẳng \[\left( {{d_2}} \right):\frac{{x – 3}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 1}}{3}\] có VTCP \[\overrightarrow {{u_2}}  = \left( { – 1;2;3} \right)\] và đi qua điểm \[{M_2}\left( {3;1;1} \right)\]

Ta có \[\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( {8; – 2;4} \right);{\mkern 1mu} \overrightarrow {{M_1}{M_2}}  = \left( { – 4; – 2; – 8} \right)\] nên

 \[\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}}  = 8.\left( { – 4} \right) + \left( { – 2} \right).\left( { – 2} \right) + 4.\left( { – 8} \right) =  – 60 \ne 0\]

Nên (d1) và (d2) chéo nhau.

Câu 19: Đáp án A

+) Điều kiện: \[\left\{ {\begin{array}{*{20}{l}}{2{x^2} – 5x + 1 > 0}\\{{{\log }_4}\left( {2{x^2} – 5x + 1} \right) \ge 0}\end{array}} \right. \Leftrightarrow 2{x^2} – 5x + 1 \ge 1\]

\[ \Leftrightarrow 2{x^2} – 5x \ge 0 \Leftrightarrow x \in \left( { – \infty ;0} \right] \cup \left[ {\frac{5}{2}; + \infty } \right)\]

+) Đặt  \[t = \sqrt {{{\log }_4}\left( {2{x^2} – 5x + 1} \right)}  = \sqrt {\frac{1}{2}{{\log }_2}\left( {2{x^2} – 5x + 1} \right)} ;\,\,\left( {t \ge 0} \right)\].

Xét \[x \ge 3\] thì \[t \ge 1\] bất phương trình tương đương với

\[ \Rightarrow 2{t^2} – m > m.t \Rightarrow m\left( {t + 1} \right) < 2{t^2} \Rightarrow m < \frac{{2{t^2}}}{{t + 1}};\forall t \ge 1\].

Xét hàm \[f\left( t \right) = \frac{{2{t^2}}}{{t + 1}}\] trên nửa khoảng \[\left[ {1; + \infty } \right)\] có:

\[f’\left( t \right) = \frac{{2{t^2} + 4t}}{{{{\left( {t + 1} \right)}^2}}} > 0;\forall t \ge 1\]. nên hàm số đồng biến trên \[\left[ {1; + \infty } \right)\].

Thỏa mãn yêu cầu bài toán \[m < f\left( 1 \right) = 1\].

Câu 20: Đáp án C

Vì \[z =  – 2 + 3i \Rightarrow M\left( { – 2;3} \right)\]

Vì N thuộc đường thẳng  y =3 nên N(a; 3)

Để \[{\rm{\Delta }}OMN\] cân tại O thì

 \[\begin{array}{l}OM = ON \Leftrightarrow O{M^2} = O{N^2}\\ \Leftrightarrow {\left( { – 2} \right)^2} + {3^2} = {a^2} + {3^2} \Leftrightarrow {a^2} = 4\end{array}\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a =  – 2 \Rightarrow N\left( {2;3} \right) \Rightarrow z = 2 + 3i}\\{a = 2 \Rightarrow N\left( { – 2;3} \right) \Rightarrow z =  – 2 + 3i}\end{array}} \right.\]

Câu 21: Đáp án A

Ta có \[{z^2} – 2z + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{z_1} = 1 + 2i}\\{{z_2} = 1 – 2i}\end{array}} \right.\].

Suy ra tọa độ \[M\left( {1;2} \right),N\left( {1; – 2} \right)\], trung điểm của đoạn MN là I(1; 0).

Câu 22: Đáp án D

Đặt \[z = a + bi\left( {a;b \in \mathbb{R}} \right)\] ta có:

 \[\begin{array}{l}\frac{{{{\left| z \right|}^2}}}{z} – \frac{{z – i}}{{1 – i}} = 3i\\ \Leftrightarrow \frac{{{a^2} + {b^2}}}{{a + bi}} – \frac{{a + bi – i}}{{1 – i}} = 3i\end{array}\]

\[ \Leftrightarrow \frac{{\left( {{a^2} + {b^2}} \right)\left( {a – bi} \right)}}{{{a^2} + {b^2}}} – \frac{{\left( {a + bi – i} \right)\left( {1 + i} \right)}}{2} = 3i\]

\[\begin{array}{l} \Leftrightarrow 2\left( {a – bi} \right) – \left( {a – b + 1} \right) – \left( {b – 1 + a} \right)i = 6i\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b – 1 = 0}\\{ – 3b – a = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b =  – 3}\end{array}} \right.\end{array}\]

Suy ra \[z = 4 – 3i \Rightarrow M\left( {4; – 3} \right)\] là điểm biểu diễn số phức z.

Khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z là OM = 5.

Câu 23: Đáp án B

Ta có \[\overrightarrow {AC}  = \left( { – 1;1;2} \right) =  – \left( {1; – 1; – 2} \right)\].

Phương trình mặt phẳng (P) qua B và vuông góc với AC là:

\[1\left( {x – 0} \right) – 1\left( {y + 1} \right) – 2\left( {z – 3} \right) = 0 \Leftrightarrow x – y – 2z + 5 = 0\].

Câu 24: Đáp án C

Gọi M(x; y), vì M  thuộc đoạn thẳng thẳng AB sao cho MA = 2MB.

 Suy ra \[\overrightarrow {AM}  = 2\overrightarrow {MB} \].

Ta có

 \[\begin{array}{l}\overrightarrow {AM}  = \left( {x;{\mkern 1mu} y + 2;{\mkern 1mu} z + 1} \right);\\2\overrightarrow {MB}  = 2\left( {1 – x;{\mkern 1mu}  – 1 – y;{\mkern 1mu} 2 – z} \right)\\ = \left( {2 – 2x;{\mkern 1mu}  – 2 – 2y;{\mkern 1mu} 4 – 2z} \right)\end{array}\]

\[\left\{ {\begin{array}{*{20}{l}}{x = 2 – 2x}\\{y + 2 =  – 2 – 2y}\\{z + 1 = 4 – 2z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{2}{3}}\\{y = \frac{{ – 4}}{3}}\\{z = 1}\end{array}} \right.\].

Vậy \[M\left( {\frac{2}{3};{\mkern 1mu} \frac{{ – 4}}{3};{\mkern 1mu} 1} \right)\]

Câu 25: Đáp án D

Gọi \[z = x + yi\].

 Ta có

 \[\begin{array}{l}\left| {z + 4 – 3i} \right| = 5\\ \Leftrightarrow \left| {\left( {x + 4} \right) + \left( {y – 3} \right)i} \right| = 5\\ \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y – 3} \right)^3} = 25\end{array}\].

Vậy biểu diễn của số phức z là đường tròn tâm \[I\left( { – 4;{\mkern 1mu} 3} \right)\], bán kính R = 5.

M là điểm biểu diễn của số phức z có mô đun lớn nhất. Khi đó M là giao điểm của đường tròn (C) và đường thẳng OI:  y = -x.

 Suy ra M( – 8; 6).

Câu 26: Đáp án C

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y= f(x); y= g(x) và các đường thẳng x= a; x= b là \[S = \mathop \smallint \limits_a^b \left| {f\left( x \right) – g\left( x \right)} \right|{\rm{d}}x\]

Câu 27: Đáp án B

Ta có \[I \in Oy \Rightarrow I\left( {0;{\mkern 1mu} b;{\mkern 1mu} 0} \right)\]

Lấy \[A\left( { – 6;{\mkern 1mu} 0;{\mkern 1mu} 0} \right) \in \left( P \right)\].

Vì

 \[\begin{array}{l}\left( P \right)//\left( Q \right)\\ \Rightarrow d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {A,\left( Q \right)} \right)\\ = \frac{{\left| { – 6 – 10} \right|}}{3} = \frac{{16}}{3}\end{array}\]

\[R = \frac{1}{2}d\left( {\left( P \right),\left( Q \right)} \right) = \frac{8}{3}\].

Mặt khác,

  \[\begin{array}{l}d\left( {I,\left( P \right)} \right) = d\left( {I,\left( Q \right)} \right)\\ \Leftrightarrow \frac{{\left| { – 2b + 6} \right|}}{3} = \frac{{\left| { – 2b – 10} \right|}}{3}\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ – 2b + 6 =  – 2b – 10}\\{ – 2b + 6 = 2b + 10}\end{array}} \right. \Rightarrow b =  – 1\end{array}\].

Nên \[I\left( {0;{\mkern 1mu}  – 1;{\mkern 1mu} 0} \right)\].

Vậy

 \[\begin{array}{l}\left( S \right):{x^2} + {\left( {y + 1} \right)^2} + {z^2} = \frac{{64}}{9}\\ \Leftrightarrow {x^2} + {y^2} + {z^2} + 2y – \frac{{55}}{9} = 0\end{array}\].

Câu 28: Đáp án D

Từ hình vẽ suy ra: Diện tích hình phẳng (H) là \[S = \mathop \smallint \limits_1^3 x\ln x{\rm{d}}x\].

Đặt \[\left\{ {\begin{array}{*{20}{l}}{u = \ln x}\\{xdx = dv}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{d}}u = \frac{1}{x}{\rm{d}}x}\\{v = \frac{{{x^2}}}{2}}\end{array}} \right.\]

Suy ra \[S = \left. {\frac{{{x^2}}}{2}\ln x} \right|_1^3 – \int\limits_1^3 {\frac{x}{2}{\rm{d}}x}  = \frac{9}{2}\ln 3 – \left. {\frac{{{x^2}}}{4}} \right|_1^3 = \frac{9}{2}\ln 3 – 2\].

Câu 29: Đáp án A

Gọi \[M\left( {{x_0};{y_0};{z_0}} \right)\] là tiếp điểm \[ \Rightarrow M \in \left( S \right)\].

Mặt cầu  (S) có tâm \[I\left( { – 1;1; – 3} \right)\], bán kính R = 4.

\[\overrightarrow {IM}  = \left( {{x_0} + 1;{y_0} – 1;{z_0} + 3} \right)\] , (P) có vtpt \[\vec n = \left( {1; – 2;2} \right)\]

Ta có

 \[\begin{array}{l}\overrightarrow {IM} .\vec n = 0\\ \Leftrightarrow {x_0} + 1 – 2{y_0} + 2 + 2{z_0} + 6 = 0\\ \Leftrightarrow {x_0} – 2{y_0} + 2{z_0} + 9 = 0\end{array}\]

⇒M thuộc mặt phẳng \[x – 2y + 2z + 9 = 0\].

Vậy tập hợp điểm cần tìm là đường tròn:

 \[{x^2} + {y^2} + {z^2} + 2x – 2y + 6z – 5 = 0;x – 2y + 2z + 9 = 0\].

Câu 30: Đáp án A

Số phức z = 3- i có phần thực bằng 3, phần ảo bằng −1

nên tổng phần thực phần ảo là 3+ (-1) = 2.

Câu 31: Đáp án A

Đặt \[u = {x^2} \Rightarrow {\rm{d}}u = 2x{\rm{d}}x;{\rm{d}}v = \frac{1}{{{{\cos }^2}x}}{\rm{d}}x \Rightarrow v = \tan x\].

\[I = \mathop \smallint \limits_0^a {\left( {\frac{x}{{\cos x}}} \right)^2}{\rm{d}}x = \left. {{x^2}\tan x} \right|_0^a – \int\limits_0^a {2x\tan x{\rm{d}}x}  = {a^2}\tan a – 2m\].

Câu 32: Đáp án B

Ta có \[z = i\left( {3i – 1} \right) = 3{i^2} – i =  – 3 – i \Rightarrow \bar z =  – 3 + i\].

Câu 33: Đáp án D

Đặt \[\left\{ {\begin{array}{*{20}{l}}{u = x}\\{{\rm{d}}v = \sin x{\rm{d}}x}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{d}}u = {\rm{d}}x}\\{v =  – \cos x}\end{array}} \right.\].

Suy ra \[\int\limits_0^\pi  {x\sin x{\rm{d}}x}  = \left. {\left( { – x\cos x} \right)} \right|_0^\pi  + \int\limits_0^\pi  {\cos x{\rm{d}}x}  = \pi  + \left. {\sin x} \right|_0^\pi  = \pi \].

Do đó \[\left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 0}\end{array}} \right. \Rightarrow a + b = 1\].

Câu 34: Đáp án D

Phương trình \[{x^2} + {y^2} + {z^2} – 2mx + 4y + 2mz + {m^2} + 5m = 0\] có

     \[a = m;b =  – 2;c = m;d = {m^2} + 5m\].

Phương trình trên là phương trình mặt cầu khi \[{a^2} + {b^2} + {c^2} – d > 0\].

\[\begin{array}{l} \Leftrightarrow {m^2} + 4 + {m^2} – \left( {{m^2} + 5m} \right) > 0\\ \Leftrightarrow {m^2} – 5m + 4 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 4}\\{m < 1}\end{array}} \right.\end{array}\]. 

Câu 35: Đáp án D

Có \[{\left( {3 + 3i} \right)^2} = {3^2} + 18i + 9{i^2} = 18i\] là một số thuần ảo nên chọn đáp án D.

Câu 36: Đáp án C

Giả sử \[w = a + bi\left( {a,b \in \mathbb{R}} \right)\].

Ta có

 \[\begin{array}{l}w = 3z – 2 + i\\ \Leftrightarrow z = \frac{{w – i + 2}}{3}\\ = \frac{{a + bi – i + 2}}{3}\\ = \frac{{a + 2}}{3} + \frac{{b – 1}}{3}i\end{array}\].

Thay \[z = \frac{{a + 2}}{3} + \frac{{b – 1}}{3}i\] vào \[\left| {z – 1 + 2i} \right| \le 2\] ta được:

  \[\begin{array}{l}\left| {\frac{{a + 2}}{3} + \frac{{b – 1}}{3}i – 1 + 2i} \right| \le 2\\ \Leftrightarrow \left| {\frac{{a – 1}}{3} + \frac{{b + 5}}{3}i} \right| \le 2\\\end{array}\]

\[ \Leftrightarrow {\left( {a – 1} \right)^2} + {\left( {b + 5} \right)^2} \le 36\]

Vậy tập hợp số phức \[w = 3z – 2 + i\] là đường tròn có bán kính bằng 6.

Diện tích hình tròn là \[{6^2}\pi  = 36\pi \].

Câu 37: Đáp án A

\[\begin{array}{l}\int\limits_0^1 {x\sqrt {{x^2} + 1} {\mkern 1mu} {\rm{d}}x}  = \frac{1}{2}\int\limits_0^1 {\sqrt {{x^2} + 1} {\mkern 1mu} {\rm{d}}\left( {{x^2} + 1} \right)} \\ = \left. {\frac{1}{3}{{\left( {\sqrt {{x^2} + 1} } \right)}^3}} \right|_0^1 = \frac{1}{3}\left( {2\sqrt 2  – 1} \right)\end{array}\].

Câu 38: Đáp án C

Tổng trên là tổng của một cấp số nhân với \[\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{q = 1 + i}\end{array}} \right.\].

 \[\begin{array}{l}z = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + … + {\left( {1 + i} \right)^{2018}}\\ \Rightarrow z = {S_{2019}} = \frac{{{u_1}\left( {1 – {q^{2019}}} \right)}}{{1 – q}}\\ \Rightarrow z = \frac{{\left( {1 – {{\left( {1 + i} \right)}^{2019}}} \right)}}{{ – i}}\end{array}\].

\[\begin{array}{l} \Rightarrow z = \frac{{\left( {1 – {{\left( {1 + i} \right)}^{2019}}} \right)}}{{ – i}}\\ \Rightarrow z = \frac{{\left[ {1 – {{\left( { – 4} \right)}^{504}}.\left( { – 2 + 2i} \right)} \right]}}{{ – i}}\\ \Rightarrow z = \frac{{\left[ {1 – {{\left( { – 4} \right)}^{504}}.\left( { – 2 + 2i} \right)} \right]}}{{ – i}}\end{array}\].

\[ \Rightarrow z = {2^{1009}} + \left( {1 + {2^{1009}}} \right)i\].

Câu 39: Đáp án A

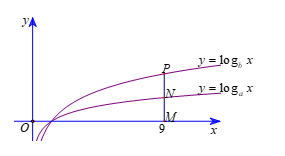
Ta có \[\left\{ {\begin{array}{*{20}{l}}{{y_N} = {\rm{lo}}{{\rm{g}}_a}9}\\{{y_P} = {\rm{lo}}{{\rm{g}}_b}9}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{y_N} = \frac{1}{{{\rm{lo}}{{\rm{g}}_9}a}}}\\{{y_P} = \frac{1}{{{\rm{lo}}{{\rm{g}}_9}b}}}\end{array}} \right.\]

Mà

 \[\begin{array}{l}{y_P} = 2{y_N}\\ \Rightarrow \frac{1}{{{\rm{lo}}{{\rm{g}}_9}b}} = 2\frac{1}{{{\rm{lo}}{{\rm{g}}_9}a}}\\ \Rightarrow {\rm{lo}}{{\rm{g}}_9}a = 2{\rm{lo}}{{\rm{g}}_9}b\\ \Rightarrow a = {b^2}\end{array}\].

Câu 40: Đáp án C

Từ đề bài, ta có: \[{V_k} = \pi  \Leftrightarrow \pi \mathop \smallint \limits_1^k \ln xdx = \pi  \Leftrightarrow \mathop \smallint \limits_1^k \ln xdx = 1\].

Đặt \[\left\{ {\begin{array}{*{20}{l}}{\ln x = u}\\{dx = dv}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{du = \frac{1}{x}dx}\\{v = x}\end{array}} \right.\].

Nên \[\mathop \smallint \limits_1^k \ln xdx = 1 \Leftrightarrow x\left. {\ln x} \right|_1^k – \int\limits_1^k {dx}  = 1\].

\[\begin{array}{l} \Leftrightarrow k\ln k – k + 1 = 1\\ \Leftrightarrow k\ln k – k = 0\\ \Leftrightarrow k\left( {\ln k – 1} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{k = 0{\mkern 1mu} {\mkern 1mu} \left( l \right)}\\{k = e}\end{array}} \right.\end{array}\]

Vậy2< k< 3.

Câu 41: Đáp án D

Phương trình \[\left( P \right):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\]

Vì a; b; c theo thứ tự tạo thành một cấp số nhân có công bội bằng 2 nên:

\[b = 2a;c = 2b = 4a\].

Suy ra: \[\frac{x}{a} + \frac{y}{{2a}} + \frac{z}{{4a}} = 1 \Leftrightarrow 4x + 2y + z = 4a\].

Mà mặt phẳng (P) đi qua điểm \[M\left( {2; – 4;1} \right)\] nên:

   \[4.2 + 2.\left( { – 4} \right) +  + 1 = 4a \Leftrightarrow a = \frac{1}{4}\].

Vậy phương trình (P) là: \[4x + 2y + z – 1 = 0\].

Câu 42: Đáp án D

Ta có: \[\overrightarrow {AB}  = \left( {0;0;2} \right);\overrightarrow {AD}  = \left( {0; – 1;2} \right)\].

Nên \[{S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right| = 2\].

Câu 43: Đáp án B

Ta có: \[\int\limits_a^b {f’\left( x \right)dx}  = f\left( b \right) – f\left( a \right) \Rightarrow f\left( b \right) – f\left( a \right) = 2\sqrt 5 \].

\[\begin{array}{l} \Rightarrow f\left( b \right) – 5 = 2\sqrt 5 \\ \Leftrightarrow f\left( b \right) = 5 + 2\sqrt 5 \\ = \sqrt 5 \left( {\sqrt 5  + 2} \right)\end{array}\]

Câu 44: Đáp án D

Xét \[\mathop \smallint \limits_0^2 f\left( {3x} \right)dx\]

Đặt \[3x = t \Leftrightarrow dx = \frac{{dt}}{3}\].

Đổi cận \[x = 0 \Rightarrow t = 0;{\mkern 1mu} x = 2 \Rightarrow t = 6\].

Ta có

 \[\begin{array}{l}\mathop \smallint \limits_0^2 f\left( {3x} \right)dx = \mathop \smallint \limits_0^6 f\left( t \right)\frac{1}{3}dt\\ = \frac{1}{3}\mathop \smallint \limits_0^6 f\left( t \right)dt\\ = \frac{1}{3}\mathop \smallint \limits_0^6 f\left( x \right)dx = \frac{1}{3}\end{array}\].

Câu 45: Đáp án A

Ta có : \[z = 3 + 2i \Rightarrow \left| z \right| = \sqrt {{3^2} + {2^2}}  = \sqrt {13} \] và \[w = 3 – 2i \Rightarrow \left| w \right| = \sqrt {{3^2} + {{\left( { – 2} \right)}^2}}  = \sqrt {13} \].

Do đó \[\left| z \right| = \left| w \right|\] nên A sai, B đúng.

Câu 46: Đáp án D

Ta có:

 \[\begin{array}{l}I = \mathop \smallint \limits_0^2 \left( {2{x^2} – x – m} \right){\rm{d}}x\\ = \left. {\left( {\frac{{2{x^3}}}{3} – \frac{{{x^2}}}{2} – mx} \right)} \right|_0^2\\ = \frac{{10}}{3} – 2m\end{array}\].

\[J = \int\limits_0^1 {\left( {{x^2} – 2mx} \right){\rm{d}}x}  = \left. {\left( {\frac{{{x^3}}}{3} – m{x^2}} \right)} \right|_0^1 = \frac{1}{3} – m\].

Để \[I \ge J \Leftrightarrow \frac{{10}}{3} – 2m \ge \frac{1}{3} – m \Leftrightarrow m \le 3\].

Câu 47: Đáp án D

Ta có:

 \[\begin{array}{l}{3^{2x + 1}} > {\left( {\frac{1}{3}} \right)^{ – 3{x^2}}}\\ \Leftrightarrow {3^{2x + 1}} > {\left( {\frac{1}{3}} \right)^{ – 3{x^2}}}\\ \Leftrightarrow 2x + 1 > 3{x^2}\end{array}\].

\[ \Leftrightarrow  – 3{x^2} + 2x + 1 > 0 \Leftrightarrow  – \frac{1}{3} < x < 1\]

Vậy tập nghiệm bất phương trình là: \[S = \left( { – \frac{1}{3};1} \right)\].

Câu 48: Đáp án A

Ta có \[\overrightarrow {AC}  = \left( { – 2;6; – 4} \right);\overrightarrow {BD}  = \left( {6;3;2} \right)\].

Gọi (P) là mặt phẳng chứa AC và song song với BD.

Suy ra Vectơ pháp tuyến của (P) là: \[\vec n = \left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right] = \left( {24; – 20; – 42} \right)\].

Chọn vectơ pháp tuyến của (P) là: \[\overrightarrow {{n_1}}  = \left( {12; – 10; – 21} \right)\]

Mặt phẳng (P) qua \[A\left( {3; – 2;1} \right)\] và nhận \[\overrightarrow {{n_1}}  = \left( {12; – 10; – 21} \right)\] làm VTPT nên phương trình tổng quát có dạng:

 \[\begin{array}{l}12\left( {x – 3} \right) – 10\left( {y + 2} \right) – 21\left( {z – 1} \right) = 0\\ \Leftrightarrow 12x – 10y – 21z – 35 = 0\end{array}\]

Câu 49: Đáp án A

Điều kiện: x> 0 .

Ta có:

 \[\begin{array}{l}\log _2^2x – {\log _2}\left( {4x} \right) < 0\\ \Leftrightarrow \log _2^2x – {\log _2}x – 2 < 0\end{array}\].

\[ \Leftrightarrow  – 1 < \,{\log _2}x < \,2 \Leftrightarrow \frac{1}{2} < x < 4\]

Mà x nguyên nên \[x \in \left\{ {1;2;3} \right\}\].

Câu 50: Đáp án B

Vì A, B, C lần lượt thuộc các trục Ox, Oy, Oz và H là trực tâm của tam giác ABC nên \[OC \bot \left( {OAB} \right) \Rightarrow OC \bot AB\] , lại có H là trực tâm của tam giác ABC nên CH ⊥ AB

Ta có: \[\left. {\begin{array}{*{20}{l}}{AB \bot OC}\\{AB \bot CH}\end{array}} \right\} \Rightarrow AB \bot \left( {OCH} \right) \Rightarrow OH \bot AB\].

Tương tự \[BC \bot OH\], từ đó \[OH \bot \left( {ABC} \right)\].

Vậy mặt phẳng (ABC) nhận \[\overrightarrow {OH}  = \left( {3;1;0} \right)\] làm vectơ pháp tuyến.

Phương trình \[\left( P \right):3\left( {x – 3} \right) + y – 1 = 0 \Leftrightarrow 3x + y – 10 = 0\].

Khoảng cách từ M đến mặt phẳng (P) là: \[d\left( {M,\left( P \right)} \right) = \frac{{\left| {3.1 + 1 – 10} \right|}}{{\sqrt {10} }} = \frac{6}{{\sqrt {10} }}\]

 

Đề thi học kì 2 Toán lớp 12 có đáp án năm 2024 (15 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2023 – 2024

Môn: Toán lớp 12

Thời gian làm bài: 90 phút

(Đề 3)

Câu 1 (NB): Trong không gian chỉ có 5 loại khối đa giác đều.

  Mệnh đề nào sau đây đúng?

A. Khối lập phương và khối bát diện đều có cùng số cạnh.               

B. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.

C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.            

D. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.

Câu 2 (NB): Trong không gian với hệ tọa độ Oxyz, cho điểm \(M(2; – 1;1).\) Tìm tọa độ điểm M ‘ là hình chiếu vuông góc của M trên mặt phẳng (Oxy).

  A. \(M'(2; – 1;0).\)      B. \(M'(0;0;1).\)        

C. \(M'( – 2;1;0).\)        D. \(M'(2;1; – 1).\)

Câu 3 (TH): Tìm tập xác định của hàm số \(y = {\left( {2 – \sqrt {x – 1} } \right)^{\sqrt 3 }}.\)

  A. \(D = \left( { – \infty ;5} \right).\) 

B. \(D = \left[ {1;5} \right).\)

C. \(D = \left[ {1;3} \right).\)

D. \(D = \left[ {1; + \infty } \right).\)         

Câu 4 (NB): Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(M(2;0; – 1)\)và có vectơ chỉ phương \(\overrightarrow a (4; – 6;2).\) Phương trình tham số của \(\Delta \) là:

  A. \(\left\{ {\begin{array}{*{20}{c}}{x =  – 2 + 4t}\\{y =  – 6t}\\{z = 1 + 2t}\end{array}} \right..\) 

B. \(\left\{ {\begin{array}{*{20}{c}}{x =  – 2 + 2t}\\{y =  – 3t}\\{z = 1 + t}\end{array}} \right..\)                           

C. \(\left\{ {\begin{array}{*{20}{c}}{x = 4 + 2t}\\{y =  – 6 – 3t}\\{z = 2 + t}\end{array}} \right..\)

D. \(\left\{ {\begin{array}{*{20}{c}}{x = 2 + 2t}\\{y =  – 3t}\\{z =  – 1 + t}\end{array}} \right..\)

Câu 5 (NB): Trong không gian với hệ tọa độ Oxyz, cho 3 điểm \(A(1;2; – 1),B( – 3;4;3),C(3;1; – 3).\) Số điểm D sao cho 4 điểm A, B, C, D là 4 đỉnh của một hình bình hành là

A. 3.                            B. 1.

C. 1.                            D. 0.

Câu 6 (NB): Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[A(1; – 2; – 1),B(1;4;3).\]Độ dài đoạn AB là:

  A. 3.                          B. \(\sqrt 6 .\)

C. \(2\sqrt 3 .\)              D. \(2\sqrt {13} .\)

Câu 7 (TH): Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số khác nhau?

  A. 328.                      B. 405.

C. 360.                        D. 500.

Câu 8 (TH): Cho hai số phức \({z_1} = 1 + 2i,{z_2} = 3 – i.\) Tìm số phức \(z = \frac{{{z_2}}}{{{z_1}}}.\)

A. \(z = \frac{1}{{10}} + \frac{7}{{10}}i.\)

B. \[z = \frac{1}{5} + \frac{7}{5}i.\]             

C. \[z = \frac{1}{5} – \frac{7}{5}i.\]             

D. \(z =  – \frac{1}{{10}} + \frac{7}{{10}}i.\)

Câu 9 (TH): F(x) là một nguyên hàm của hàm số \(f(x) = 3{x^2} + \frac{1}{{2x + 1}}.\) Biết \(F(0) = 0,F(1) = a + \frac{b}{c}\ln 3\) trong đó a, b, c là các số nguyên dương và \(\frac{b}{c}\) là phân số tối giản. Khi đó, giá trị biểu thức a+ b + c bằng

  A. 4.                          B. 3.

C. 12.                          D. 9

Câu 10 (TH): Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu (S)có tâm \(I(0;1; – 1)\) và tiếp xúc với mặt phẳng \((P):2x – y + 2z – 3 = 0.\)

A. \({x^2} + {(y + 1)^2} + {(z + 1)^2} = 4.\)

 B. \({x^2} + {(y + 1)^2} + {(z – 1)^2} = 4.\) 

C. \({x^2} + {(y – 1)^2} + {(z + 1)^2} = 4.\)

D. \({x^2} + {(y – 1)^2} + {(z + 1)^2} = 2.\)

Câu 11 (TH): Thể tích khối tròn xoay sinh ra bởi phép quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^{\frac{x}{2}}},\) trục hoành, trục tung và đường thẳng x =2 bằng

A. \(\pi {e^2}.\)            B. \(\pi ({e^2} – 1).\)

C. \(\pi (e – 1).\)            D. \({e^2} – 1.\)

Câu 12 (TH): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA \bot (ABCD),\)SC tạo với đáy một góc 600. Tính thể tích V của khối chóp đã cho.  

  A. \(V = \frac{{{a^3}\sqrt 6 }}{6}.\)

B. \(V = \frac{{{a^3}\sqrt 3 }}{6}.\)

C. \(V = \frac{{{a^3}\sqrt 6 }}{3}.\)   

D. \(V = \frac{{{a^3}\sqrt 3 }}{3}.\)

Câu 13 (NB): Phương trình \({4^{2x – 4}} = 16\) có nghiệm là:  

  A. x= 3                      B.x= 2

C.x= 4                         D. x= 1

Câu 14 (TH): Cho tứ diện đều ABCD. Gọi \(\varphi \) là góc giữa đường thẳng AB và mặt phẳng (BCD). Tính \(\cos \varphi .\)

A. \(\cos \varphi  = \frac{1}{2}.\)   

B. \(\cos \varphi  = 0.\) 

C. \[\cos \varphi  = \frac{{\sqrt 2 }}{3}.\] 

D. \[\cos \varphi  = \frac{{\sqrt 3 }}{3}.\]

Câu 15 (NB): Trong các mệnh đề sau, mệnh đề nào đúng?  

  A. Số phức \(z = 2 – 3i\) có phần thực là 2 và phần ảo là -3i.           

  B. Số phức \(z = 2 – 3i\) có phần thực là 2 và phần ảo là – 3.           

  C. Số phức\(z = 2 – 3i\)  có phần thực là 2 và phần ảo là 3i.            

  D. Số phức\(z = 2 – 3i\) có phần thực là 2 và phần ảo là 3

Câu 16 (NB): Hàm số nào sau đây đồng biến trên khoảng (-1; 1).

  A. \(y = {x^2}.\)

B. \(y =  – {x^3} + 3x.\)

C. \(y = \sqrt {1 – {x^2}} .\)   

D. \(y = \frac{{x + 1}}{x}.\)

Câu 17 (NB): Cho hàm số y= f(x) có bảng biến thiên như hình vẽ

 

 

 

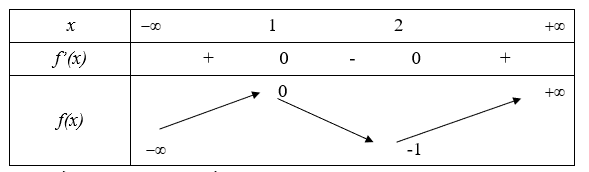
Hàm số có giá trị cực đại bằng

  A. 1.                          B. 2. 

C. 0.                          D. -1.

Câu 18 (TH): Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \((S):x{}^2 + {y^2} + {z^2} – 2(x + 2y + 3z) = 0.\) Gọi A, B, C lần lượt là giao điểm ( khác gốc tọa độ O) của mặt cầu (S)và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC)là:  

A. \(6x – 3y – 2z – 12 = 0.\)

B. \(6x + 3y + 2z – 12 = 0.\)                           

C. \(6x – 3y – 2z + 12 = 0.\)

D. \(6x – 3y + 2z – 12 = 0.\)

Câu 19 (TH): Khoảng cách giữa hai tiệm cận đứng của đồ thị hàm số \(y = \frac{1}{{{x^2} – 2}}\) bằng:  

A. 2.                            B. \(\sqrt 2 .\)

C. \(2\sqrt 2 .\)              D. 4.

Câu 20 (TH): Giá trị nhỏ nhất của hàm số \(y =  – {x^4} + {4^2} – 5\) trên đoạn \(\left[ { – 2;3} \right]\) bằng:

  A. -5.                         B. -50.

C. -1.                           D. -197.

Câu 21 (NB): Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường x=a; x= b(a< b) (phần tô đậm trong hình vẽ) tính theo công thức:

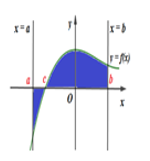
A. \(S = \int\limits_a^c {f(x)dx + } \int\limits_c^b {f(x)dx} .\)

B. \(S = \int\limits_a^b {f(x)dx} .\)                

C. \(S = \left| {\int\limits_a^b {f(x)dx} } \right|.\)                            

D. \(S =  – \int\limits_a^c {f(x)dx + } \int\limits_c^b {f(x)dx} .\)

Câu 22 (NB): Đường cong hình bên là đồ thị của hàm số nào sau đây?

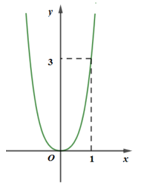
A. \(y =  – {x^4} + 4{x^2}.\)   

B. \(y = {x^2}.\)        

C. \(y = 2{x^4} + {x^2}.\)   

D. \(y = 3{x^4} – {x^2} + 1.\)

Câu 23 (NB): Trong các khẳng định sau, khẳng định nào sai?  

A. \({\left( {1 – \frac{{\sqrt 2 }}{2}} \right)^{2018}} < {\left( {1 – \frac{{\sqrt 2 }}{2}} \right)^{2017}}.\)

B. \({2^{\sqrt 2  + 1}} > {2^{\sqrt 3 }}.\)       

C. \({\left( {\sqrt 2  – 1} \right)^{2017}} > {\left( {\sqrt 2  – 1} \right)^{2018}}.\)

D. \({\left( {\sqrt 3  – 1} \right)^{2018}} > {\left( {\sqrt 3  – 1} \right)^{2017}}.\)

Câu 24 (NB): Cho các số nguyên dương \(k,n,k < n.\) Mệnh đề nào sau đây sai?  

  A. \(C_n^k = \frac{{n!}}{{(n – k)!}}.\)

B. \(A_n^k = k!.C_n^k.\)      

C. \(C_n^{n – k} = C_n^k.\)   

D. \(C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}.\)

Câu 25 (TH): Có bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { – 14;15} \right]\) sao cho đường thẳng y= mx+ 3 cắt đồ thị của hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) tại hai điểm phân biệt  

  A. 17.                        B. 16.

C. 20.                          D. 15.

Câu 26 (NB): Mệnh đề nào sau đây đúng?  

A. Hàm số y= sinx đồng biến trên \(\left( {0;\frac{\pi }{2}} \right).\)  

B. Đồ thị hàm số y=sinx có tiệm cận ngang.  

C. Hàm số y= sinx tuần hoàn với chu kì \(T = \pi .\)                         

D. Hàm số y= sinx là hàm số chẵn.

Câu 27 (VD): Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B’C’. Mặt phẳng (A’MN) cắt cạnh BC tại P. thể tích khối đa diện MBP.A’B’N’ là:

A. \(\frac{{\sqrt 3 {a^3}}}{{24}}.\) 

B. \(\frac{{7\sqrt 3 {a^3}}}{{96}}.\)        

C. \(\frac{{\sqrt 3 {a^3}}}{{12}}.\) 

D. \(\frac{{7\sqrt 3 {a^3}}}{{32}}.\)

Câu 28 (TH): Cho hàm số y= f(x) có bảng biến thiên như hình vẽ

 

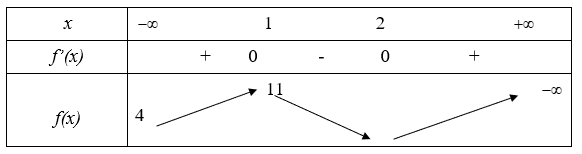
Đồ thị hàm số \(y = \left| {f(x) – 2m} \right|\) có 5 điểm cực trị khi và chỉ khi

  A. \(m \in \left( {4;11} \right).\)   

B. \(m \in \left[ {2;\frac{{11}}{2}} \right].\)

C. \(m \in \left( {2;\frac{{11}}{2}} \right).\)

D. m = 3

Câu 29 (VD): Biết rằng bất phương trình

\[m\left( {\left| x \right| + \sqrt {1 – {x^2}}  + 1} \right) \le 2\sqrt {{x^2} – {x^4}}  + \sqrt {{x^2}}  + \sqrt {1 – {x^2}}  + 2\] có nghiệm khi và chỉ khi \(m \in \left( { – \infty ;a\sqrt 2  + b} \right]\) . Tính T= a+ b    

A.  T = 0                      B. T = 1

C. T= 2                        D.  T= 3

Câu 30 (VD): Cho hàm số\(y = \frac{{x + 2}}{{x – 2}}\) có đồ thị là (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến của (C) cắt hai đường tiệm cận của (C) tại hai điểm A, B. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác IAB bằng  

  A. \(2\pi .\)                 B. \(8\pi .\)

C. \(4\sqrt 2 \pi .\)         D. \(4\pi .\)

Câu 31 (VD): Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác góc A là \(\frac{x}{1} = \frac{{y – 6}}{{ – 4}} = \frac{{z – 6}}{{ – 3}}.\) Biết rằng điểm \(M(0;5;3)\) thuộc đường thẳng AB và điểm N(1; 1; 0) thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC ?

 A. \(\overrightarrow u (1;2;3).\)   

B. \(\overrightarrow u (0; – 2;6).\)    

C. \(\overrightarrow u (0;1; – 3).\)   

D. \(\overrightarrow u (0;1;3).\)

Câu 32 (VD): Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a mét (a chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi đường kính của hình bán nguyệt). Gọi d là đường kính của hình bán nguyệt. Hãy xác định d để diện tích cửa sổ là lớn nhất.

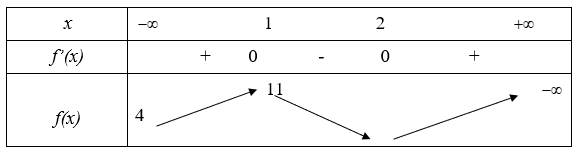
A. \(d = \frac{a}{{4 + \pi }}.\)   

B. \(d = \frac{{2a}}{{4 + \pi }}.\)   

C. \(d = \frac{a}{{2 + \pi }}.\)   

D. \(d = \frac{{2a}}{{2 + \pi }}.\)

Câu 33 (VD): Cho hình chop S.ABC có đáy là tam giác ABC vuông tại A;\(\widehat {ABC} = {30^0}\) tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).

A. \(h = \frac{{2a\sqrt {39} }}{{13}}.\)

B. \(h = \frac{{a\sqrt {39} }}{{13}}.\)     

C. \(h = \frac{{a\sqrt {39} }}{{26}}.\)

D. \(h = \frac{{a\sqrt {39} }}{{52}}.\)

Câu 34 (VD): Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn \(\frac{z}{{16}}\) và  \(\frac{{16}}{{\overline z }}\)có phần thực và phần ảo đều thuộc đoạn \(\left[ {0;1} \right].\) Tính diện tích S của (H).

A. S = 256   

B. \(S = 64\pi .\)        

C. \(S = 16(4 – \pi ).\) 

D. \(S = 32(6 – \pi ).\)

Câu 35 (VD): Biết tích phân \(\int\limits_0^{\ln 6} {\frac{{{e^x}}}{{1 + \sqrt {{e^x} + 3} }}} dx = a + b\ln 2 + c\ln 3\) với a; b ;c là các số nguyên dương. Tính T =a + b + c

A.  T = 2                      B. T = 1

C.T = 0                        D. T=-1

Câu 36 (VD): Cho hàm số y= f(x) có đạo hàm liên tục trên đoạn \(\left[ {0;\frac{\pi }{4}} \right]\) và \(f\left( {\frac{\pi }{4}} \right) = 0.\)

Biết \(\int\limits_0^{\frac{\pi }{4}} {{f^2}} (x)dx = \frac{\pi }{8},\int\limits_0^{\frac{\pi }{4}} {{f^’}} (x)sin2xdx =  – \frac{\pi }{4}.\) Tính tích phân \(I = \int\limits_0^{\frac{\pi }{8}} {f(2x)dx.} \)  

A. \(I = \frac{1}{2}.\)     

B. \(I = \frac{1}{4}.\) C. I = 2 D. I = 1

Câu 37 (TH): Tìm tập hợp tất cả các giá trị thực của m để phương trình \(1 + {\log _5}({x^2} + 1) = {\log _5}(m{x^2} + 4x + m)\) có hai nghiệm phân biệt.

  A. \(m \in (3;7)\backslash \left\{ 5 \right\}.\)

B. \(m \in (3;7).\)

C. \(m \in R\backslash \left\{ 5 \right\}.\)

D. \(m \in R\)

Câu 38 (TH): Biết  \(\int\limits_e^{{e^4}} {f(\ln x)\frac{1}{x}} dx = 4.\)Tính tích phân \(I = \int\limits_1^4 {f(x)dx.} \)

  A.I = 8                       B.I= 16

C. I = 2                        D. I = 4

Câu 39 (TH): Cho khai triển \({(1 – 4x)^{18}} = {a_0} + {a_1}x + … + {a_{18}}{x^{18}}.\) Giá trị của \({a_3}\) bằng

  A. -52224.                 B. 52224.

C. 2448.                      D. -2448.

Câu 40 (VD): Cho các số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2.\) Gọi M, N lần lượt là điểm biểu diễn các số phức \({z_1},i{z_2}\). Biết rằng \(\)\(\widehat {MON} = {60^0}\). Tính \(T = \left| {z_1^2 + 9z_2^2} \right|.\)

  A. \(T = 36\sqrt 2 .\)   B. \(T = 24\sqrt 3 .\)

C. \(T = 36\sqrt 3 .\)      D. \(T = 18.\)

Câu 41: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;2} \right]\) bằng 2. Số phần tử của tập S là:

  A. 3.                          B. 1.

C. 4.                            D. 2.

Câu 42 (TH): Cho hàm số y= f(x) liên tục trên R. Biết rằng hàm số y= f’(x) có đồ thị như hình vẽ. Hàm số \(y = f({x^2} – 5)\)nghịch biến trên khoảng nào sau đây?

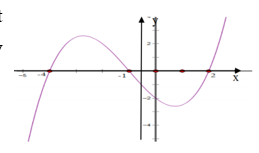
  A. ( -1;0)                    B.(1; 2)                     

  C.(-1; 1)                    D. (0; 1)

Câu 43 (VD): Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Hỏi rằng ông A phải gửi ngân hàng mỗi tháng số tiền gần nhất với số tiền nào sau đây? Biết lãi suất hằng tháng là 0,5%, tiền lãi sinh ra hằng tháng được nhập vào tiền vốn, số tiền gửi hàng tháng là như nhau.  

A. \(a = 14.261.000\) đồng.

B. \(a = 14.260.500\) đồng.

C. \(a = 14.261.500\) đồng.

D. \(a = 14.260.000\) đồng.

Câu 44 (VD): Cho dãy số (un) xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_{n + 1}} = {u_n} + {n^3},\forall n \in N*}\end{array}} \right..\) Tìm số nguyên dương n nhỏ nhất sao cho\[\sqrt {{u_n} – 1}  \ge 2039190.\]

A. n = 2017                  B. n = 2020

C. n = 2018                  D. n = 2019

Câu 45 (VD): Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng (SAB),(SBC),(SCD),(SDA) với mặt đáy lần lượt là \({90^0},{60^0},{60^0},{60^0}.\) Biết rằng tam giác SAB vuông cân tại S, AB = avà chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp S.ABCD.  

A. \(V = \frac{{{a^3}\sqrt 3 }}{4}.\)

B. \(V = {a^3}\sqrt 3 .\)

C. \(V = \frac{{2{a^3}\sqrt 3 }}{9}.\) 

D. \(V = \frac{{{a^3}\sqrt 3 }}{9}.\)

Câu 46 (VD): Cho hàm số y= f(x) liên tục trên \(\left[ {1;4} \right]\) và thỏa mãn \(f(x) = \frac{{f(2\sqrt x  – 1)}}{{\sqrt x }} + \frac{{\ln x}}{x}.\) Tính tích phân \(I = \int\limits_3^4 {f(x)dx.} \)  

A. \(I = 2{\ln ^2}2.\)

B. \(I = 2\ln 2.\)

C. \(I = 3 + 2{\ln ^2}2.\)     

D. \(I = {\ln ^2}2.\)

Câu 47 (VD): Trong không gian với hệ tọa độ Oxyz, cho điểm \(A(1;2; – 3)\) và mặt phẳng \((P):2x + 2y – z + 9 = 0.\) Đường thẳng đi qua A và vuông góc với mặt phẳng \((Q):3x + 4y – 4z + 5 = 0\) cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Tính độ dài MB.

A. \(MB = \sqrt 5 .\)

B. \(MB = \frac{{\sqrt 5 }}{2}.\)

C. \(MB = \frac{{\sqrt {41} }}{2}.\) 

D. \(MB = \sqrt {41} .\)

Câu 48 (VD): Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật. \(AB = a,AD = a\sqrt 3 .\) Hình chiếu vuông góc của điểm A’ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B’ đến (A’BD) .  

A. \(\frac{{a\sqrt 3 }}{3}.\)   

B. \(\frac{{a\sqrt 3 }}{4}.\)

C. \(\frac{{a\sqrt 3 }}{2}.\)     

D. \(\frac{{a\sqrt 3 }}{6}.\)

Câu 49 (TH): Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài 3 đội bóng củaViệt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để ba đội Việt Nam ở 3 bảng khác nhau.  

 A. \(\frac{{16}}{{55}}.\) 

B. \(\frac{{133}}{{165}}.\)

C. \(\frac{{32}}{{165}}.\)   

D. \(\frac{{39}}{{65}}.\)

Câu 50 (VD): Hình nón đỉnh S, đáy là hình tròn nội tiếp tam giác ABC. Biết rằng AB = BC = 10a, AC = 12a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 450. Tính thể tích V của khối nón đã cho.  

A. \(V = 9\pi {a^3}.\)    B. \(V = 12\pi {a^3}.\)

C. \(V = 27\pi {a^3}.\)  D. \(V = 3\pi {a^3}.\)

ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT ĐỀ SỐ 3

 

1. A	2.A	3. B	4. D	5. D	6. D	7. A	8. C	9. A	10. C
11. B	12. C	13. A	14. D	15. B	16. B	17. C	18. B	19. C	20. B
21. D	22. C	23. D	24. A	25. A	26. A	27. B	28. C	29. B	30. C
31. D	32. B	33. B	34. D	35. C	36. B	37. A	38. D	39. A	40. C
41. D	42. D	43. C	44. B	45. D	46. A	47. A	48. C	49. A	50. A