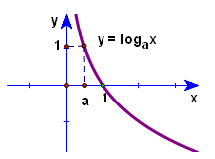Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
112 BÀI TẬP CHUYÊN ĐỀ MŨ – LOGARIT
LÝ THUYẾT + BÀI TẬP PHÂN CHIA THEO CẤP ĐỘ
I. LŨY THỪA
1. Lũy thừa với số mũ nguyên
– Lũy thừa với số mũ nguyên dương
\({a^n} = \mathop a\limits_{\,\,nts} a \ldots a\left( {a \in \mathbb{R},n \in {\mathbb{N}^*}} \right){\rm{. }}\)
– Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
\({a^{ – n}} = \frac{1}{{{a^n}}}\left( {n \in {Z^ + },a \in {\rm{R}}\backslash \{ 0\} } \right);{a^0} = 1.\)
– Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.
2. Căn bậc n
Cho số thực b và số nguyên dương \(n \ge 2\).
Số a được gọi là căn bậc n của b nếu \({a^n} = b\)
– Khi n lẻ, \(\forall b\) thì tồn tại duy nhất \(\sqrt[n]{b}\);
– Khi n chẵn và
+b<0 : không tồn tại căn bậc n của b;
+ b=0 : có 1 căn bậc n của b là \(\sqrt[n]{0} = 0\);
+ b>0 : có hai căn bậc n của số b là \(\sqrt[n]{b} > 0\) và \( – \sqrt[n]{b} < 0\).
3. Lũy thừa với số mũ hữu tỷ
Cho số thực a>0 và số hữu tý \(r = \frac{m}{n}\) trong đó \(m \in Z,n \in Z,n \ge 2\). Khi đó
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
4. Lũy thừa với số mũ vô tỷ
Cho \(a > 0,\alpha \in {\rm{R}}\backslash Q\) và \(\left( {{r_n}} \right)\) là 1 dãy số vô tỷ sao cho \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Khi đó
\({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\)
5. Các tính chất
– Cho hai số dương a, b và \(m,n \in {\rm{R}}\). Khi đó
\({a^m} \cdot {a^n} = {a^{m + n}}\)
\({\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m} = {a^{m \cdot n}}\)
\(\frac{{{a^m}}}{{{a^n}}} = {a^{m – n}}\)
\({(a.b)^n} = {a^n}{b^n}\)
\({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\)
– So sánh hai lũy thừa
Nếu \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
Nếu \(0 < a < 1\) thì \({a^m} > {a^n} \Leftrightarrow m < n\)
Nếu \(0 < a < b\) thì \({a^m} < {b^m} \Leftrightarrow m > 0\)
Nếu \(0 < a < b\) thì \({a^m} > {b^m} \Leftrightarrow m < 0\)
II.HÀM SỐ LŨY THỪA
1. Định nghĩa. Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) được gọi là hàm số lũy thừa
2. Tâp xác địhh.
Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) có tập xác định là
– \({\rm{R}}\) nếu \(\alpha \) nguyên dương.
– \({\rm{R}}\backslash \{ 0\} \) nếu \(\alpha \) nguyên âm hoặc \(\alpha = 0\).
– \((0; + \infty )\) nếu \(\alpha \) không nguyên.
3. Đạo hàm.
– Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) có đạo hàm với mọi \(x > 0\) và \({\left( {{x^\alpha }} \right)^\prime } = \alpha {x^{\alpha – 1}}\).
– Với hàm hợp \(y = {u^\alpha }\) (với \(u = u(x)\) ta có \({\left( {{u^\alpha }} \right)^\prime } = \alpha \cdot {u^{\alpha – 1}} \cdot {u^\prime }\quad (u > 0,\alpha \in {\rm{R}})\)
4. Khảo sát hàm số lũy thừa trên
|
|
|
\(\alpha < 0\) |
|
Đạo hàm |
\(y’ = \alpha .{x^{\alpha – 1}}\) |
\(y’ = \alpha .{x^{\alpha – 1}}\) |
|
Chiều biến thiên |
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) |
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) |
|
Tiệm cận |
Không có |
Tiệm cận ngang Ox Tiệm cận đứng Oy |
|
Đồ thị |
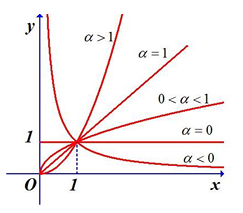
Đồ thị hàm số luôn đi qua điểm (1;1) |
|
– Hình sau là đồ thị hàm số lũy thừa trên \(\left( {0; + \infty } \right)\)ứng với các giá trị khác nhau của α
III. LOGARIT
1. Định nghĩa. Cho hai số dương a, b thỏa mãn \(a > 0;a \ne 1;b > 0\). Số \(\alpha \) thỏa mãn \({a^\alpha } = b\) được gọi là logarit cơ số a của b. Kí hiệu \(\alpha = {\log _a}b\).
\({\log _a}b = \alpha \Leftrightarrow {a^a} = b\)
2. Các tính chất và quy tắc tính
Với \(a > 0;a \ne 1;b > 0;{b_1} > 0;{b_2} > 0;c > 0;c \ne 1\) ta có
– \({\log _a}1 = 0\)
– \({\log _a}a = 1\)
– \({\log _a}{a^b} = b\)
– \({a^{{{\log }_a}\alpha }} = \alpha ,(\alpha > 0)\)
– \({\log _a}\left( {{b_1} \cdot {b_2}} \right) = {\log _a}{b_1} + {\log _a}{b_2}\)
– \({\log _a}\left( {\frac{{{b_1}}}{{{b_2}}}} \right) = {\log _a}{b_1} – {\log _a}{b_2}\)
– \({\log _a}{b^a} = \alpha \cdot {\log _a}b\)
– \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\)
Đặc biệt: \({\log _a}{N^{2n}} = 2n \cdot {\log _a}|N|\)
– \({\log _c}b = {\log _c}a \cdot {\log _a}b\)
– \({\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
– \({\log _a}b = \frac{1}{{{{\log }_b}a}}(b \ne 1)\)
– \({\log _{{a^k}}}N = \frac{1}{k}{\log _a}N(k \ne 0,N > 0)\)
– \({a^{{{\log }_b}c}} = {c^{{{\log }_b}a}}\)
IV. HẢM SỐ MŨ
1. Định nghĩa. Hàm số \(y = {a^x}(a > 0,a \ne 1)\) được gọi là hàm số mũ cơ số a.
2. Giới hạn và đạo hàm của hàm số mũ
a. Giới hạn cần nhớ: \(\mathop {\lim }\limits_{t \to 0} \frac{{{e^t} – 1}}{t} = 1\)
b. Đạo hàm của hàm số mũ. Hàm số \(y = {a^x}\quad ({\rm{a}} > 0,{\rm{a}} \ne 1)\) có đạo hàm tại mọi x
– \({\left( {{e^x}} \right)^\prime } = {e^x}\)
– \({\left( {{e^u}} \right)^\prime } = {u^\prime }{e^u}\)
– \({\left( {{a^x}} \right)^\prime } = {a^x}\ln a\quad ({\rm{a}} > 0,{\rm{a}} \ne 1)\)
– \({\left( {{a^u}} \right)^\prime } = {u^\prime } \cdot {a^u}\ln a\)
|
|
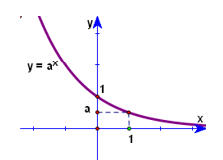
0<a<1 |
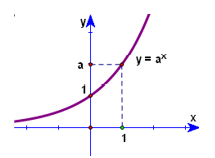
a>1 |
|
|
Tập xác định |
D=R |
D=R |
|
|
Tập giá trị |
T=R+ |
T=R+ |
|
|
Chiều biến thiên |
Hàm số nghịch biến trên R |
Hàm số đồng biến trên R |
|
|
Tiệm cận |
Đồ thị nhận Ox làm tiệm cận ngang |
||
|
Đồ thị |
Đồ thị luôn đi qua các điểm (0;1) và (1;a) nằm phía trên trục hoành Ox |
||
|
|
|
|
|
V. HÀM SÓ LOGARIT
1. Định nghĩa. Hàm số \(y = {\log _a}x\quad (a > 0,a \ne 1)\) được gọi là hàm số logarit cơ số a.
2. Đạo hàm của hàm số logarit
Hàm số \(y = {\log _a}x\) (.) có đạo hàm tại mọi x>0
– \({\left( {{{\log }_a}x} \right)^\prime } = \frac{1}{{x\ln a}}\)
– \({\left( {{{\log }_a}u} \right)^\prime } = \frac{{{u^\prime }}}{{u\ln a}}\)
– \({(\ln x)^\prime } = \frac{1}{x}\)
\({(\ln u)^\prime } = \frac{{{u^\prime }}}{u}\)
3. Các tính chất của hàm số logarit
|
|
0<a<1 |
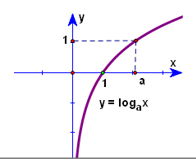
a>1 |
|
|
Tập xác định |
\(D = \left( {0; + \infty } \right)\) |
\(D = \left( {0; + \infty } \right)\) |
|
|
Tập giá trị |
T=R |
T=R |
|
|
Chiều biến thiên |
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) |
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) |
|
|
Tiệm cận |
Đồ thị nhận Oy làm tiệm cận ngang |
||
|
Đồ thị |
Đồ thị luôn đi qua các điểm (1;0) và (a;1) nằm phía bên phải trục Oy |
||
|
|
|
|
|
Xem thêm