Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Hàm số lũy thừa, hàm số mũ, hàm số Logarit Toán lớp 12, tài liệu bao gồm 90 trang, tổng hợp 8 chủ đề về Hàm số lũy thừa, hàm số mũ, hàm số Logarit đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án và lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Lý thuyết, bài tập về Hàm số lũy thừa, hàm số mũ, hàm số Logarit có đáp án gồm các nội dung sau:
A. HÀM SỐ LŨY THỪA
1. Lý thuyết về hàm số lũy thừa
a. Định nghĩa: Hàm số y = xα với α ∈ R được gọi là hàm số lũy thừa.
b. Tập xác định: Tập xác định của hàm số y = xα là:
• D = R nếu α là số nguyên dương.
• D = R \ {0} với α nguyên âm hoặc bằng 0
• D = (0; +∝) với α không nguyên.
c. Đạo hàm: Hàm số y = xα có đạo hàm với mọi x > 0 và (xα)’ = α.xα – 1.
d. Tính chất của hàm số lũy thừa trên khoảng (0; +∝).
| y = xα, α > 0 | y = xα, α < 0 |
| Tập khảo sát: (0; +∝) | Tập khảo sát: (0; +∝) |
|
Sự biến thiên + y’ = αxα – 1 > 0, ∀x > 0 + Giới hạn đặc biệt + Tiệm cận: không có |
Sự biến thiên + y’ = αxα – 1 < 0, ∀x > 0 + Giới hạn đặc biệt + Tiệm cận: không có – Trục 0x là tiệm cận ngang – Trục 0y là tiệm cận đứng. |
| Bảng biến thiên |
c. Bảng biến thiên |
Đồ thị:
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm I(1; 1)
Lưu ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: y = x3, y = x-2, y = xπ
2. Bài tập về hàm số lũy thừa
Câu 1. Tính đạo hàm của hàm số 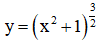

Hướng dẫn:
Chọn D
Ta có:
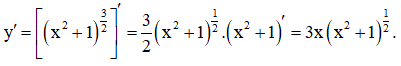
Câu 2. Cho hàm số y = (2x2 + 4x + 1)√3. Khi đó đạo hàm y’(0) bằng
A. 4√3 .
B. 0.
C. 12√3
D. 28.
Hướng dẫn:
Chọn A
y = (2x2 + 4x + 1)√3 => y’(x) = √3.(4x + 4).(2x2 + 4x + 1)√3-1 => y’(0) = 4√3
Câu 3. Cho hàm số y = (x + 2)-2. Gọi y’’ là đạo hàm cấp hai của hàm số y trên tập xác định của hàm số. Khẳng định nào sau đây là đúng?
A. 2y’’ – 3y = 0.
B. (y’’)2 – 4y = 0 .
C. 2y’’ + 2y = 0.
D. y’’ + 6y2 = 0.
Hướng dẫn:
Chọn D
Ta có:
y = (x + 2)-2 => y‘ = -2(x + 2)-3
=> y’’ = 6(x + 2)-4 = 0.
Suy ra 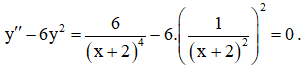
B. HÀM SỐ MŨ
1. Lý thuyết Hàm số mũ
a. Hàm số mũ: y = ax, (a > 0, a ≠ 1)
a.1 Tập xác định: D = R
a.2. Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = af(x) thì t > 0
a.3. Tính đơn điệu:
+ Khi a > 1 thì hàm số y = ax đồng biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) > g(x).
+ Khi 0 < a < 1 thì hàm số y = ax nghịch biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) < g(x).
a.4. Đạo hàm:
(ax)’ = ax.ln a ⇒ (au)’ = u’.au.ln a
(ex)’ = ex ⇒ (eu)’ = eu.u’
a.5. Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.
b. Hàm số logarit: y = logax, (a > 0, a ≠ 1)
b.1 Tập xác định: D = (0; +∝)
b.2. Tập giá trị: T = R, nghĩa là khi giải phương trình logarit mà đặt t = logax thì t không có điều kiện.
b.3. Tính đơn điệu:
+ Khi a > 1 thì y = logax đồng biến trên D khi đó nếu: logaf(x) > logag(x) ⇔ f(x) > g(x).
+ Khi 0 < a < 1 thì y = logax nghịch biến trên D khi đó nếu logaf(x) > logag(x) ⇔ f(x) < g(x).
b.4 Đạo hàm:
b.5. Đồ thị: Nhận trục tung làm đường tiệm cận đứng.
2. Bài tập về Hàm số mũ
Bài 1: Biết 4x + 4-x = 23 tính giá trị của biểu thức P = 2x + 2-x :
Hướng dẫn:
Bài 2: Tìm khoảng đồng biến, nghịch biến của hàm số
Hướng dẫn:
Ta có bảng biến thiên
Vậy hàm số đồng biến trên khoảng (-∞; 1)
Hàm số nghịch biến trên khoảng (1; +∞)
Bài 3: Cho hàm số y = eax2+bx+c đạt cực trị tại x = 1 và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x=2.
Hướng dẫn:
+ Cắt Oy tại y=e nên c=1.
+ y’=(ax+b) eax2+bx+c . Mà y'(1)=0 ⇔2a+b=0
+ Khi đó y(2) = e4a+2b+c = e.
C. HÀM SỐ LOGARIT
1. Lý thuyết về hàm số logarit: y = logax, (a > 0, a ≠ 1)
a. Tập xác định: D = (0; +∝)
b. Tập giá trị: T = R, nghĩa là khi giải phương trình logarit mà đặt t = logax thì t không có điều kiện.
c. Tính đơn điệu:
+ Khi a > 1 thì y = logax đồng biến trên D khi đó nếu: logaf(x) > logag(x) ⇔ f(x) > g(x).
+ Khi 0 < a < 1 thì y = logax nghịch biến trên D khi đó nếu logaf(x) > logag(x) ⇔ f(x) < g(x).
d. Đạo hàm:
e. Đồ thị: Nhận trục tung làm đường tiệm cận đứng.
2. Bài tập về Hàm số logarit
Bài 1: Tìm cực trị của hàm số y = log2(x3-4x)
Hướng dẫn:
Vẽ bảng biến thiên, khi đó hàm số có 1 cực trị
Bài 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = log2(x2-2x+3) trên đoạn [-1;2]
Hướng dẫn:
Bài 3: Tìm tập giá trị T của hàm số f(x)=(lnx)/x với x ∈ [1;e2 ].
Hướng dẫn:
Hàm số f(x) xác định và liên tục trên đoạn [1;e2].
Xem thêm