Bài 2: Hình chóp tứ giác đều

Giải SBT Toán 8 Bài 2: Hình chóp tứ giác đều

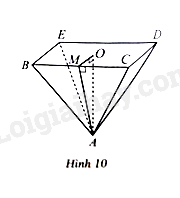
Bài 7 trang 76 SBT Toán 8 Tập 1: Cho hình chóp tứ giác đều $A.BCDE$ có $AO$ là chiều cao, $AM$ là trung đoạn (Hình 10). Trong các phát biểu sau phát biểu nào sai?

a) Mặt đáy $BCDE$ là hình vuông.

b) Các mặt bên $ABC,ADC,ADE,AEB$ là những tam giác cân tại $A$

c)  $AM\mathrm{\perp }BC$

d) $AO>AM$

 

Lời giải:

Phát biểu a, b và c đúng

Phát biểu d sai vì xét $\mathrm{\Delta }AOM$ có: $OA\mathrm{\perp }OM$ nên $AOM$ là tam giác vuông có $AM$ là cạnh huyền, mà cạnh huyền luôn lớn hơn cạnh góc vuông.

Bài 8 trang 76 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?

a) Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

b) Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với chiều cao.

c) Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với độ dài trung đoạn.

d) Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Lời giải:

Phát biểu a, d là đúng. Phát biểu b, c là sai.

Bài 9 trang 77 SBT Toán 8 Tập 1: Cho hình chóp tứ giác đều có diện tích xung quanh bằng $192c{m}^2$ và độ dài trung đoạn bằng 8 cm. Tính độ dài cạnh đáy của hình chóp tứ giác đều đó.

Lời giải:

Áp dụng công thức $S_{xq}=\frac{1}{2}.C.d$, trong đó $S_{xq}$ là diện tích xung quanh, $C$ là chu vi đáy, $d$ là độ dài trung đoạn của hình chóp tứ giác đều, ta có: $192=\frac{1}{2}.C.8$

Suy ra $C=48\left(cm\right)$

Vậy độ dài cạnh đáy của hình chóp tứ giác đều đó là: $48:4=12$ (cm).

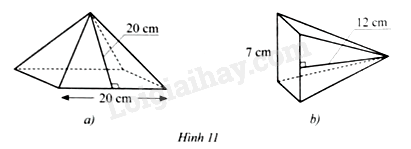
Bài 10 trang 77 SBT Toán 8 Tập 1: Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 11a; 11b;

 

Lời giải:

Diện tích xung quanh của hình chóp tứ giác đều ở Hình 11a là:

$\frac{1}{2}.\left(20.4\right).20=800\left(c{m}^2\right)$

Diện tích xung quanh của hình chóp tứ giác đều ở Hình 11b là:

$\frac{1}{2}.\left(7.4\right).12=168\left(c{m}^2\right)$

Bài 11 trang 77 SBT Toán 8 Tập 1: Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước Công nguyên. Kim tự tháp này có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 231 m và chiều cao khoảng 146,5 m. Tính thể tích của kim tự tháp đó.

Lời giải:

Áp dụng công thức tính thể tích của hình chóp tứ giác đều: $V=\frac{1}{3}.S.h$, trong đó $V$ là thể tích, $S$ là diện tích đáy, $h$ là chiều cao của hình chóp tứ giác đều, ta có thể tích của kim tự tháp Kheops là:

$\frac{1}{3}{.231}^2.146,5=2605795,5\left(m^3\right)$

Bài 12 trang 77 SBT Toán 8 Tập 1: Cho hình chóp tứ giác đều có thể tích bằng $1,4m^3$ và chiều cao bằng 42 dm. Tính độ dài cạnh đáy của hình chóp tứ giác đều đó.

Lời giải:

Áp dụng công thức $V=\frac{1}{3}.S.h$, trong đó $V$ là thể tích, $S$ là diện tích đáy, $h$ là chiều cao của hình chóp tứ giác đều, ta có: $1400=\frac{1}{3}.S.42$

Suy ra $S=100\left(d{m}^2\right)$.

Vậy độ dài cạnh đáy của hình chóp tứ giác đều đó là: $\sqrt{100}=10$ (dm)

Bài 13 trang 77 SBT Toán 8 Tập 1: Cho hình chóp tứ giác đều có thể tích bằng $0,675m^3$ và độ dài cạnh đáy bằng 1,5 m. Tính chiều cao của hình chóp tứ giác đều đó.

Lời giải:

Áp dụng công thức tính thể tích của hình chóp tứ giác đều ta có:

$V=\frac{1}{3}.S.h$. Suy ra: $0,675=\frac{1}{3}.\left(1,5.1,5\right).h$

Vậy $h=0,9m$ .

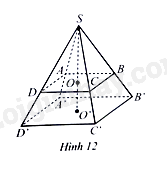
Bài 14 trang 77 SBT Toán 8 Tập 1: Cho hai hình chóp tứ giác đều $S.ABCD$ và $S.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ lần lượt có chiều cao $SO$ và $S{O}^{\prime }$. Biết $AB=2a,A^{\prime }{B}^{\prime }=3a,SO=2b,S{O}^{\prime }=3b$ (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều $S.ABCD$ và $S.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ biết rẳng $a$ và $b$ cùng đơn vị đo.

 

Lời giải:

Thể tích của hình chóp tứ giác đều $S.ABCD$ là:

$\frac{1}{3}.\left(2a.2a\right).2b=\frac{8a^{2}b}{3}$ (đơn vị thể tích)

Thể tích của hình chóp tứ giác đều $S.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ là:

$\frac{1}{3}.\left(3a.3a\right).3b=9a^{2}b$ (đơn vị thể tích)

Tỉ số thể tích của hình chóp tứ giác đều $S.ABCD$ và $S.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ là:

$\frac{8a^{2}b}{3}:\left(9a^{2}b\right)=\frac{8}{27}$

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4

Bài 1: Định lí Pythagore

Bài 2: Tứ giác